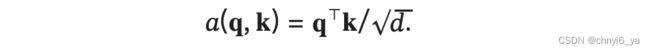90. 注意力分数及代码实现

1. 注意力分数

2. 拓展到高维度

3. Additive Attention

ps： 这种的好处是，key，value，query的长度可以不一样

4. Scaled Dot-Product Attention

• n个query，m个key-value 对
• 最后的结果是n x m的矩阵，第i行就表示第i个权重query是什么样的
• 然后对每一行做 softmax，最后和v去乘
• 对m个键值对查询n次，每次查询得到一个值，最终得到n个值

5. 总结

• 注意力分数是query和key的相似度，注意力权重是对分数做softmax结果
• 两种常见的分数计算：
  • 将query和key合并起来进入一个单输出单隐藏层的MLP
  • 直接将query和key做内积

6. 代码实现

本节将介绍两个流行的评分函数，稍后将用他们来实现更复杂的注意力机制。

import math
import torch
from torch import nn
from d2l import torch as d2l

6.1 掩蔽softmax操作

正如上面提到的，softmax操作用于输出一个概率分布作为注意力权重。 在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。 为了仅将有意义的词元作为值来获取注意力汇聚， 可以指定一个有效序列长度（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。 下面的masked_softmax函数实现了这样的掩蔽softmax操作（masked softmax operation）， 其中任何超出有效长度的位置都被掩蔽并置为0。

def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        # 正常的softmax
        return nn.functional.softmax(X, dim=-1)
    else:
    	# 以下用torch.rand(2, 2, 4)来举例解释代码：
        shape = X.shape # shape=(2,2,4)
        if valid_lens.dim() == 1: # ([2, 3])的维度是1
        	# repeat_interleave()中有3个参数：
        	# 第一个参数：代表复制多少次，第二个参数：每个元素的重复次数
        	# 第三个参数：需要重复的维度。默认情况下dim=None，
        	# 表示将把给定的输入张量展平（flatten）为向量
        	# 这里表示，把[2,3]重复 shape[1]=2次，展平成数组[2,2,3,3]
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
        	# reshape(-1)把tensor展开成一个行向量
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        # 函数运行返回得到的X是4*4的矩阵，并且进行了mask操作
        return nn.functional.softmax(X.reshape(shape), dim=-1)

为了演示此函数是如何工作的， 考虑由两个 2×4 矩阵表示的样本， 这两个样本的有效长度分别为 2 和 3 。 经过掩蔽softmax操作，超出有效长度的值都被掩蔽为0。

masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))

运行结果：

同样，也可以使用二维张量，为矩阵样本中的每一行指定有效长度。

masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))

运行结果：

6.2 加性注意力

加性注意力的评分函数：

Linear输入和输出的维度可以是任意，即不论你是二维，还是三维，甚至是 n 维度都是可以的。这里，通过 nn.Linear 后的输出形状除了最后一个维度，其他的均与输出一样，且这个输出值不会有任何变化。比如 [1， 2，5] 形状的张量，通过 nn.Linear(5, 18) 的线性层，其输出的形状是 [1, 2, 18]，函数内部用到的原理是高维矩阵与低维矩阵相乘和高维矩阵与低维矩阵相加。

class AdditiveAttention(nn.Module):
    """加性注意力"""
    # h：num_hiddens，k：key_size，q：query_size
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        # bia为false，因为不需要bias
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
      # valid_lens ：有多少对 key-value pair是需要的
      # valid_lens的长度和query的长度是一样的
      # 因为W_q和W_k都是nn.Linear（）函数的返回值
      # 相当于:对W_q传入一个形状为[batch_size,valid_lens，query_size]的值，经过线性层
      # 返回一个 形状为[batch_size,valid_lens，num_hiddens]的tensor
        queries, keys = self.W_q(queries), self.W_k(keys)
      # 因此，queries和keys的形状都是：[batch_size,valid_lens，num_hiddens]
      
        # 之后，通过unsqueeze函数进行维度扩展。
        # queries的形状：(batch_size，查询的个数，1，num_hiddens)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        # unsqueeze(2)：在第2个维度加1
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        # features的特征：(batch_size，查询的个数，“键－值”对的个数，num_hiddens)
        features = torch.tanh(features) 
        
        # 将features传入self.w_v得到的输出的形状是：
        # (batch_size，查询的个数，“键－值”对的个数，1)
        # 通过squeeze(-1) 把最后一个维度移除
        # 因此，scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1) 
        # 对scores做softmax得到注意力权重
        self.attention_weights = masked_softmax(scores, valid_lens)
        # attention_weights的形状：(batch_size，查询的个数，“键-值”对的个数)
        
        # values的形状：(batch_size，“键－值”对的个数，value的长度/特征个数)
        # 对attention_weights做dropout，也就是对masked之后的weight做dropout
        # 也就告诉了哪些key-value 不用看
        # dropout是保证了sacle的，所有项加起来是等于1的，只是把更多项变成了0
        # 最后的size为（批量数、q的个数、v的长度）
        # torch.bmm函数作用：两个三维矩阵的乘法，但有特殊的规定
        # 相乘的两个张量，要像如下的对应维度一样：
        # ma: [a, b, c]
		# mb: [a, c, d] 最后相乘的shape维[a, b, d]
        return torch.bmm(self.dropout(self.attention_weights), values)

用一个小例子来演示上面的AdditiveAttention类， 其中查询、键和值的形状为（批量大小，步数或词元序列长度，特征大小）， 实际输出为 (2,1,20) 、 (2,10,2) 和 (2,10,4) 。 注意力汇聚输出的形状为（批量大小，查询的步数，值的维度）。

queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
# 形状为(1, 10, 4)之后repeat(2,1,1)做的操作是：
# 在第0维上复制2次，在第1维上复制1次，在第二维上复制1次
# ps：copy一次就是照搬，复制2次是double
# 也就是repeat后变成了(2,10,4)
# keys和values的第1维都是10，也就是说，key-value pair 有10个，即步数为10个
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(
    2, 1, 1)
# 第一个样本去看前两个key-value pair，第二个样本去看前6个key-value pair
valid_lens = torch.tensor([2, 6])

attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
                              dropout=0.1)
attention.eval()
attention(queries, keys, values, valid_lens)

运行结果：

尽管加性注意力包含了可学习的参数，但由于本例子中每个键都是相同的，都是1， 所以注意力权重是均匀的，由指定的有效长度决定。

# attention.attention_weights的形状是（2，1，10）
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')

运行结果，对attention_weights进行可视化：

6.3 缩放点积注意力

使用点积可以得到计算效率更高的评分函数， 但是点积操作要求查询和键具有相同的长度 。 假设查询和键的所有元素都是独立的随机变量， 并且都满足零均值和单位方差， 那么两个向量的点积的均值为 0 ，方差为 。 为确保无论向量长度如何， 点积的方差在不考虑向量长度的情况下仍然是 1 ， 我们再将点积除以 根号d， 则缩放点积注意力（scaled dot-product attention）评分函数为：

下面的缩放点积注意力的实现使用了暂退法进行模型正则化。

class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        # .shape得到(batch_size，查询的个数，d)
        # 再通过-1得到d
        d = queries.shape[-1] 
        # 设置transpose_b=True为了交换keys的最后两个维度
        # keys.transpose(1,2)交换第1维度和第2维度，那么形状就变成了：
        # (batch_size，d，“键－值”对的个数) 和queries进行相乘后，
        # 得到的score的形状是：(batch_size，查询的个数，“键－值”对的个数)
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        # attention_weights的形状和scores的形状一样：
        # (batch_size，查询的个数，“键－值”对的个数)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # 再和value(batch_size，“键－值”对的个数，值的维度)相乘
        # 返回的张量形状是(batch_size，查询的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)

为了演示上述的DotProductAttention类， 我们使用与先前加性注意力例子中相同的键、值和有效长度。 对于点积操作，我们令查询的特征维度与键的特征维度大小相同。

queries = torch.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.eval()
attention(queries, keys, values, valid_lens)

运行结果：

与加性注意力演示相同，由于键包含的是相同的元素， 而这些元素无法通过任何查询进行区分，因此获得了均匀的注意力权重。

d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
                  xlabel='Keys', ylabel='Queries')

运行结果：

7. Q&A

Q1:怎么理解注意力分数？

A1:使用一个具体的例子，k是公司员工，v是公司员工的薪水，q是自己，通过注意力去依次和公司员工比较，大致算出自己能得到的薪水。