【数据结构与算法学习笔记-BST二叉查找树】
本文为学习笔记,感兴趣的读者可在MOOC中搜索《数据结构与算法Python版》或阅读《数据结构(C语言版)》(严蔚敏)
目录链接:https://blog.csdn.net/floating_heart/article/details/123991211
区别于静态查找表,动态查找表的特点是,表结构本身实在查找过程中动态生成的,即对于给定值的key,若表中存在其关键字等于key的记录,则查找成功返回,否则插入关键字等于key的记录。
4.2 二叉查找树Binary Search Tree
4.2.1 初识BST
此处引用《数据结构C语言版》中对二叉查找树的定义(书中为二叉排序树Binary Sort Tree,是二叉查找树的不同称谓):
二叉排序树(Binary Sort Tree)或者是一棵空树;或者是具有下列性质的二叉树:
(1)若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值;
(2)若它的右子树不空,则右子树上所有结点的值均大于它的根节点的值;
(3)它的左、右子树分别为二叉排序树。
很明显,这一定义也是遵循递归结构的定义方式,下面给出一个构建BST的例子(取自“数据结构与算法 Python版”):
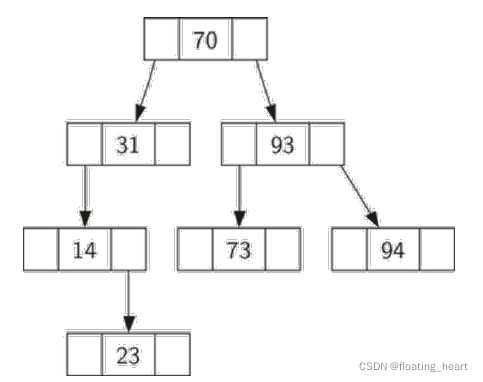
示例:BST的构建
- 按照70,31,93,94,14,23,73的顺序插入。
- 首先插入的70成为树根(root)
- 31比70小,放到左子节点
- 93比70大,放到右子节点
- 94比93大,放到右子节点
- 14比31小,放到左子节点
- 23比14大,放到其右
- 73比93小,放到其左
- 获得如下结构
- 注意:插入顺序不同,生成的BST也不同
由于建立BST的过程进行了初步的大小比较,所以在后续查找或搜索的时候复杂度会有一定程度的降低。下面对BST的定义和操作进行说明。
4.2.2 BST的定义和部分操作
存储方式:
一般来说,采用二叉链表作为BST的存储结构。
此处采用“数据结构与算法Python版”中的实现方案,同样以链表为存储结构,采用BST和TreeNode两个类:BST的root成员引用根节点TreeNode;TreeNode类存储链表中单个结点的内容。
下面就一些定义和简单操作以Python代码的方式进行展示。
BST:
class BinarySearchTree:
# 初始化
def __init__(self) -> None:
self.root = None
self.size = 0
# 返回大小size
def length(self):
return self.size
# 封装len()方法
def __len__(self):
return self.size
# 返回迭代器
def __iter__(self):
return self.root.__iter__()
BinarySearchTree类比较简洁,封装了一些常用方法,保存了到节点类的链接和二叉搜索树的大小。
TreeNode:
class TreeNode:
def __init__(self,key,val,left=None,right=None,parent=None) -> None:
self.key = key # 键值
self.payload = val # 数据项
self.leftChild = left # 左子节点
self.rightChild = right # 右子节点
self.parent = parent # 父节点
def hasLeftChild(self):
return self.leftChild
def hasRightChild(self):
return self.rightChild
def isLeftChild(self):
return self.parent and self.parent.leftChild == self
def isRightChild(self):
return self.parent and self.parent.rightChild == self
def isRoot(self):
return not self.parent
def isLeaf(self):
return not (self.rightChild or self.leftChild)
def hasAnyChildren(self):
return self.rightChild or self.leftChild
def hasBothChildren(self):
return self.rightChild and self.leftChild
TreeNode类中保存了键值、数据项和向上向下的链接,目前提供了包括替换节点在内的常用方法,替换节点方法会在后面删除节点的操作中使用。
4.2.3 插入方法BST.put(key,val)
增加新结点,该方法在
BinarySearchTree类中
首先看BST是否为空,如果一个节点都没有,那么key成为根节点root;
否则,就调用一个递归函数(私有)_put(key, val, root)来放置key。
# 插入结点 put方法
def put(self,key,val):
if self.root: #有根节点,调用_put()方法
self._put(key,val,self.root)
else: #空树,新节点为根节点
self.root = TreeNode(key,val)
self.size += 1 # 树的大小加1
_put(key, val, currentNode)函数(私有)采用递归的方式,插入新结点:
- 如果key比
currentNode小,那么_put到左子树:如果没有左子树,那么key就成为左子节点 - 如果key比
currentNode大,那么_put到右子树:如果没有右子树,那么key就成为右子节点
# put中_put方法(私有)
def _put(self,key,val,currentNode):
if key < currentNode.key: # key比currentNode.key小,递归左子树
if currentNode.hasLeftChild():
self._put(key,val,currentNode.leftChild)
else:
currentNode.leftChild = TreeNode(key,val,parent=currentNode)
else: # key比currentNode.key大,递归右子树
if currentNode.hasRightChild():
self._put(key,val,currentNode.rightChild)
else:
currentNode.rightChild = TreeNode(key,val,parent=currentNode)
插入方法完成后,索引赋值方法即可实现:
# 索引赋值方法
def __setitem__(self,key,val):
self.put(key,val)
之后可以通过索引的方式进行赋值,如:
mytree = BinarySearchTree()
mytree[1] = 'red'
mytree[2] = 'yellow'
mytree[5] = 'blue'
mytree[4] = 'pink'
4.2.4 查找方法BST.get(key)
根据key查找结点:在树中找到key所在的结点取到payload(val)
与put()方法类似:
- 如果树不为空,从根节点开始,调用_get()方法查找,根据查找的结果进行返回;
- 如果树为空,直接返回None
# 根据key查找结点 get方法
def get(self,key):
if self.root:
res = self._get(key,self.root)
if res:
return res.payload
else:
return None
else:
return None
_get(key, currentNode)方法(私有函数)采用递归的方式,从某一结点开始查找:
- 如果
currentNode为None,返回None; - 如果key等于
currentNode.key,返回currentNode; - 如果key小于
currentNode.key,进入currentNode左子节点调用自身; - 如果key大于
currentNode.key,进入currentNode右子节点调用自身。
# get中的_get方法 私有函数
def _get(self,key,currentNode):
if not currentNode:
return None
elif key == currentNode.key:
return currentNode
elif key < currentNode.key:
return self._get(key,currentNode.leftChild)
else:
return self._get(key,currentNode.rightChild)
此处currentNode为None时,私有函数_get()也会返回None,所以在get()方法中可以去掉对self.root是否存在的判断。为了展示完整思路,此处暂不去除。
查找方法完成之后,通过索引取值和’in’操作即可实现。
# 通过索引取值
def __getitem__(self,key):
return self.get(key)
# in操作
def __contains__(self,key):
if self._get(key,self.root):
return True
else:
return False
实现了索引取值和‘in’操作后,可实现如下操作:
# 继上一个例子之后
print(mytree[1]) # red
print(mytree[2]) # yellow
print(1 in mytree) # True
print(6 in mytree) # False
4.2.5 完善迭代器
此处我们将类中的迭代器完善一下:
BST中__iter__()方法代码如下:
def __iter__(self):
return self.root.__iter__()
此处我们需要在TreeNode类中完善__iter__()方法,代码如下:
# 迭代器 中序遍历
def __iter__(self):
if self:
if self.hasLeftChild():
for elem in self.leftChild:
yield elem
yield self.key
if self.hasRightChild():
for elem in self.rightChild:
yield elem
很明显,此处采用的遍历方法为中序遍历。迭代器完成后,我们就可以用for循环枚举BST类中所有key值,配合之前完善的索引取值,我们可以更好地展示此功能:
for key in mytree:
print(key,mytree[key])
# 1 red
# 2 yellow
# 4 pink
# 5 blue
4.2.6 删除方法BST.delete(key)
删除节点是几个方法中相对最难的方法,方法的思路如下:
首先,用_get()找到要删除的节点,然后调用remove来删除,找不到则提示错误。
# 删除
def delete(self,key):
if self.size > 1:
nodeToRemove = self._get(key,self.root)
if nodeToRemove:
self.remove(nodeToRemove)
self.size -= 1
else:
raise KeyError('Error, key not in tree')
elif self.size == 1 and self.root.key == key:
self.root = None
self.size -= 1
else:
raise KeyError('Error, key not in tree')
此处把大量的操作放在了remove()中,在remove的时候需要考虑三种情况:这个节点没有子节点、有1个子节点和有2个子节点。下面分别进行说明:
-
没有子节点:直接删除该节点即可(在delete函数中已经考虑了没有子节点且为根节点的情况,所以此处只可能是叶子节点;为了完整性,此处笔者还是加入了根节点的判断)。
-
有1个子节点:将子节点上移替换掉被删节点即可,当然,此时需要考虑被删节点和其子节点究竟是左子节点、右子节点还是根节点,以方便移动节点:
- 若被删节点不是根节点,则判断被删节点和其子节点分别是左子节点还是右子节点,然后建立被删节点的parent节点和被删节点的子节点的"连接"即可;
- 若被删节点是根节点,因为根节点没有parent节点,所以不像其他情况一样需要建立parent节点与子节点的联系,只需要用子节点替换根节点即可,此处预先定义了该情况下节点替换的方法
TreeNode.replaceNodeData()。
-
有2个子节点:选择合适的节点进行替换,比如“后继”,即被删节点右子树中key值最小的节点。将“后继”摘出(删除),换到被删节点的位置(将被删节点的key和payload替换)。这样看来其“前驱”(被删节点左子树中key值最大的节点)应该也可以,下面的代码采用“后继”的替换方案。此处预先定义了寻找后继节点的方法
TreeNode.findSuccessor()。
相关代码如下:
# delete中的remove方法
def remove(self,currentNode):
# 情况一:没有子节点
if not currentNode.hasAnyChildren():
if currentNode.isLeaf(): # 是叶节点
if currentNode.isLeftChild():
currentNode.parent.leftChild = None
else:
currentNode.parent.rightChild = None
else: # 是根节点
# (这是笔者自己加的,为了保证remove函数的完整性,这段操作在delete()函数中已经考虑了)
currentNode = None
# 情况三:有两个子节点
elif currentNode.hasBothChildren():
succ = currentNode.findSuccessor()
self.remove(succ)
currentNode.key = succ.key
currentNode.payload = succ.payload
# 情况二:有一个子节点
else:
if currentNode.hasLeftChild(): # currentNode有左子树
if currentNode.isLeftChild(): # currentNode是左子树
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.leftChild
elif currentNode.isRightChild(): # currentNode是右子树
currentNode.leftChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.leftChild
else: # currentNode是根节点
# currentNode的内容替换为其左子节点的内容
currentNode.replaceNodeData(currentNode.leftChild.key,currentNode.leftChild.payload,\
currentNode.leftChild.leftChild,currentNode.leftChild.rightChild)
else: # currentNode有右子树
if currentNode.isLeftChild(): # currentNode是左子树
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.leftChild = currentNode.rightChild
elif currentNode.isRightChild(): # currentNode是右子树
currentNode.rightChild.parent = currentNode.parent
currentNode.parent.rightChild = currentNode.rightChild
else: # currentNode是根节点
# currentNode的内容替换为其右子节点的内容
currentNode.replaceNodeData(currentNode.rightChild.key,currentNode.rightChild.payload,\
currentNode.rightChild.leftChild,currentNode.rightChild.rightChild)
remove()函数的代码虽多,但多是各种情况的讨论,在前面的文字分析之后并不复杂。下面对两个预先定义的方法进行说明:
TreeNode.replaceNodeData()方法在TreeNode类中,由被删节点调用,适用于被删节点只有一个子节点时被删节点时根节点的情况,用该子节点替换根节点:
# 替换根节点
def replaceNodeData(self,key,value,lc,rc):
# key,value,lc,rc分别为新的key值,value(payload)值,左子树(leftChild)和右子树(rightChild)
self.key = key
self.payload = value
self.leftChild = lc
self.rightChild = rc
# 此时leftChild和rightChild已经加载完成
# 如果存在子节点,则将子节点的parent连接到该节点中
if self.hasLeftChild():
self.leftChild.parent = self
if self.hasRightChild():
self.rightChild.parent = self
TreeNode.findSuccessor()方法同样在TreeNode类中,由A节点调用,返回A节点右子树的key值最小的节点(A节点的“后继”),适用于被删节点有两个子节点的情况:
# 寻找后继节点
def findSuccessor(self):
succ = None
if self.hasRightChild():
succ = self.rightChild
while succ.hasLeftChild():
succ = succ.leftChild
return succ
删除方法完成后,del操作即可实现:
# 特殊方法 del操作
def __delitem__(self,key):
self.delete(key)
__delitem__方法定义之后,del操作即可实现,如下所示:
del mytree[2]
for key in mytree:
print(key,mytree[key])
# 1 red
# 4 pink
# 5 blue
读者可以自行测试del方法,此处选择了有两个子节点的最复杂情况进行展示。
此处代码和《数据结构Python版》中的代码有所不同,一方面是
TreeNode.findSuccessor()寻找后继节点方法中,仅给出了符合示例要求的情况没考虑其他情况;另一方面是remove()方法中,有两个子节点的情况,获得后继节点之后删除后继节点,笔记选择调用自身remove()方法,自觉更加方便直观,课程中新写了一个函数进行操作。感兴趣的读者可以看下文:原部分的展示# 原findSuccessor()函数 def finSuccessor(self): succ = None if self.hasRightChild(): succ = self.rightChild.findMin() else: if self.parent: if self.isLeftChild(): succ = self.parent else: self.parent.rightChild = None succ = self.parent.findSuccessor() self.parent.rightChild = self return succ def findMin(self): current = self while current.hasLeftChild(): current = current.leftChild return current# 原remove()函数中有两个子节点的情况 elif currentNode.hasBothCHildren(): succ = currentNode.finSuccessor() succ .spliceOut() currentNode.key = succ.key currentNode.payload = succ.payload # spliceOut()函数 def spliceOut(self): if self.isLeaf(): if self.isLeftChild(): self.parent.leftChild = None else: self.parent.rightChild = None elif self.hasAnyCHildren(): if self.hasLeftChild(): if self.isLeftCHild(): self.parent.leftChild = self.leftChild else: self.parent.rightChild = self.leftChild self.leftCHild.parent = self.parent else: if self.isLeftCHild(): self.parent.leftChild = self.rightChild else: self.parent.rightChild = self.rightChild self.rightChidl.parent = self.parent
4.2.7 算法复杂度分析
BST的性能和二叉搜索树的高度直接相关,其高度又受到插入顺序的影响:
- 如果key的列表随机分布的话,大于和小与根节点key的键值大致相等,BST的高度则为 l o g 2 n log_2n log2n,以put()方法为例,其最差性能为 O ( l o g 2 n ) O(log_2n) O(log2n)。
- 如果key分布极端情况下,树的高度为n,此时put()方法最差性能是 O ( n ) O(n) O(n)。
基于此,一种BST的改进型,平衡二叉树(AVL树)被提出。这将放在下一节进行介绍。