数据预处理方法
文章目录
- 1. 数据归一化
- 2. 剔除异常值
- 3. 对比训练集测试集
- 4. 相关性分析
- 5. 多重共线性分析
-
- 5.1 判别标准
- 5.2 PCA解决共线性
- 6. 构造特征
- 7. 探究数据分布
-
- 7.1 Q-Q图和P-P图
- 7.2 Box-Cox变换
在机器学习或深度学习对数据进行预处理时可以从下列因素进行考虑。
1. 数据归一化
将数据进行归一化后训练速度能够提升,减小迭代的次数。
2. 剔除异常值
画出各个特征的箱型图,箱型图能够很直观的看出异常值,将过于离散的点直接丢弃即可,代码如下
import pandas as pd
import matplotlib.pyplot as plt
#读取文件
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
# 画出箱型图
plt.figure(figsize=(18, 10))
plt.boxplot(x=train_data.values,labels=train_data.columns)
#画出上下边缘的线,更能够直观看出异常值
plt.hlines([-7.5, 7.5], 0, 40, colors='r')
plt.show()
使用pandas语句筛选出符合条件的数据行,如
train_data = train_data[train_data['V9']>-7.5]
该语句能够将 V9 这一列的数据中不符合大于-7.5的数据整行剔除。
3. 对比训练集测试集
将训练集和测试集的各个特征的数据画出来,如果训练集和测试集的某些特征的数据分布十分不一致,波动极大,那么说明这些特征的会影响模型的泛化能力,将这些特征进行删除。
在这里使用的图是核密度估计图,是概率论上用来估计未知的密度函数,属于非参数检验,通过核密度估计图可以比较直观的看出样本数据本身的分布特征。
代码如下:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
plt.figure(figsize=(10, 5))
ax = sns.kdeplot(train_data["V0"], color="Red", shade=True)
ax = sns.kdeplot(test_data["V0"], color="Blue", shade=True)
ax.set_xlabel("V0")
ax.set_ylabel("Frequency")
ax = ax.legend(["train", "test"])
plt.show()
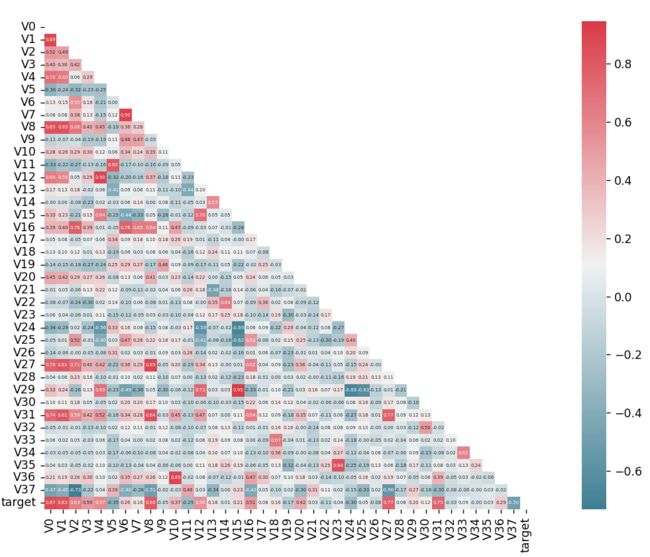
4. 相关性分析
计算每个特征与目标值的相关系数,删除相关系数小的特征,认为其与目标值无关。示例代码如下:
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
# 读取文件
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
plt.figure(figsize=(20, 16))
column = train_data.columns.tolist()
mcorr = train_data[column].corr(method="spearman")
# 遮住对称矩阵的另一边
mask = np.zeros_like(mcorr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# 分散颜色,依次是起始、终止颜色值,as_cmap 返回一个 matplotlib colormap 而不是一个颜色列表。
cmap = sns.diverging_palette(220, 10, as_cmap=True)
# 画出热力图
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f', annot_kws={"fontsize":4})
plt.show()
5. 多重共线性分析
多重共线性即多个自变量之间有很强的线性关系,比如 x 1 = 2 x 2 x_1=2x_2 x1=2x2,这样的话就无法固定其他变量,无法找到因变量与自变量的准确关系。比如,如果 x 1 = 2 x 2 x_1=2x_2 x1=2x2 拟合后的结果是 y = 2 x 1 + 2 x 2 y=2x_1+2x_2 y=2x1+2x2,那么 y = 3 x 1 y=3x_1 y=3x1 与 y = 2.1 x 1 + 1.8 x 2 y=2.1x_1+1.8x_2 y=2.1x1+1.8x2 得到的结果是一样的,而如果测试集里面并不存在严格的 x 1 = 2 x 2 x_1=2x_2 x1=2x2,那么拟合的两条直线是 y = 3 x 1 y=3x_1 y=3x1 还是 y = 2.1 x 1 + 1.8 x 2 y=2.1x_1+1.8x_2 y=2.1x1+1.8x2 就显然有区别了,这就造成了因变量对自变量无法准确定义的问题,这就是多重共线性以及其造成的后果。
在处理数据时,要尽量避免多重共线性。
5.1 判别标准
一般使用方差膨胀因子(VIF)来对多重共线性进行评定,VIF值越大,多重共线性越严重。一般认为VIF大于10时(严格是5),代表模型存在严重的共线性问题。
有时候也会以容差值作为标准,容差值=1/VIF,所以容差值大于0.1则说明没有共线性(严格是大于0.2),VIF和容差值有逻辑对应关系,两个指标任选其一即可。
多重共线性的解决有很多种方法,像逐步分析法、岭回归、主成分分析、删除不重要的信息等,这里我主要介绍下主成分分析法(PCA)。
5.2 PCA解决共线性
使用PCA能够很好地解决多重共线性的问题,缺点之一在于经过PCA过后的数据失去了可解释性,示例如下:
from sklearn.decomposition import PCA #主成分分析法
import pandas as pd
# 数据读取
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
#PCA方法降维
#保持90%的信息
pca = PCA(n_components=0.8)
# 降维后的数组是numpy类型
new_train_pca_90 = pca.fit_transform(train_data.iloc[:,0:-1])
# 测试集也需要一并降维
new_test_pca_90 = pca.transform(test_data)
# 转为pandas类型
new_train_pca_90 = pd.DataFrame(new_train_pca_90)
new_test_pca_90 = pd.DataFrame(new_test_pca_90)
new_train_pca_90['target'] = train_data['target']
6. 构造特征
当拥有的特征或特征数据过少的时候可以选择该方法自己构造特征,以此增加数据量,类似于CV中的数据增强,示例如下:
import pandas as pd
from sklearn.decomposition import PCA #主成分分析法
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
import lightgbm as lgb
import numpy as np
# 读取数据
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
epsilon=1e-5
#组交叉特征,可以自行定义,如增加: x*x/y, log(x)/y 等等
func_dict = {
'add': lambda x,y: x+y,
'mins': lambda x,y: x-y,
'div': lambda x,y: x/(y+epsilon),
'multi': lambda x,y: x*y
}
a = [train_data,test_data]
def auto_features_make(train_data,test_data,func_dict,col_list):
'''
特征构造
:param train_data: 训练集
:param test_data: 测试集
:param func_dict: 变换的函数
:param col_list: 列名的列表
:return: 变换后的训练集、测试集
'''
train_data, test_data = train_data.copy(), test_data.copy()
# 下面对两个列名的循环是将任意组合的两个列交叉
for col_i in col_list:
for col_j in col_list:
for func_name, func in func_dict.items():
for data in [train_data,test_data]:
func_features = func(data[col_i],data[col_j])
col_func_features = '-'.join([col_i,func_name,col_j])
data[col_func_features] = func_features
return train_data,test_data
# 构造特征数据
train_data2, test_data2 = auto_features_make(train_data,test_data,func_dict,col_list=test_data.columns)
7. 探究数据分布
线性回归时若数据不服从正态分布,不对称分布可能会导致模型扭曲,会给线性回归的最小二乘估计系数的结果带来误差,所以需要对数据进行结构化转换。
7.1 Q-Q图和P-P图
可以使用Q-Q图以及P-P来对数据与正态分布的吻合性进行探究。
P-P图:P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图,用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布,则代表样本数据的点应当基本在代表理论分布的对角线上。
Q-Q图:Q-Q图的结果与P-P图非常相似,只是P-P图是用分布的累计比,而Q-Q图用的是分布的分位数来做检验。和P-P图一样,如果数据为正态分布,则在Q-Q正态分布图中,数据点应基本在图中对角线上。
总之,不管是P-P图还是Q-Q图,只需要看散点与直线的重合程度即可。Q-Q图示例代码如下:
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
# 读取数据
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
plt.figure(figsize=(10,5))
ax=plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax=plt.subplot(1,2,2)
res = stats.probplot(train_data['V0'], plot=plt)
plt.show()
7.2 Box-Cox变换
解决上述问题的一个方法是使用Box-Cox转换将数据转换为正态,目的是得到正态分布的数据(转换后)和稳定的方差。,这里同样不对原理进行细讲,代码示例如下:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from sklearn import preprocessing
import numpy as np
# 读取数据
train_data_file = "data/zhengqi_train.txt"
test_data_file = "data/zhengqi_test.txt"
data_train = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
data_test = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
data_train["oringin"]="train"
data_test["oringin"]="test"
data_all=pd.concat([data_train,data_test],axis=0,ignore_index=True)
# 归一化
cols_numeric=list(data_all.columns)
cols_numeric.remove("oringin")
def scale_minmax(col):
return (col-col.min())/(col.max()-col.min())
scale_cols = [col for col in cols_numeric if col!='target']
data_all[scale_cols] = data_all[scale_cols].apply(scale_minmax,axis=0)
plt.figure(figsize=(10,7))
i = 0
var = "V10"
if var != 'target':
dat = data_all[[var, 'target']].dropna()
plt.subplot(2, 2, 1)
sns.distplot(dat[var], fit=stats.norm);
plt.title(var + ' Original')
plt.xlabel('')
plt.subplot(2, 2, 2)
_ = stats.probplot(dat[var], plot=plt)
plt.title('skew=' + '{:.4f}'.format(stats.skew(dat[var])))
plt.xlabel('')
plt.ylabel('')
plt.subplot(2, 2, 3)
trans_var, lambda_var = stats.boxcox(dat[var].dropna() + 1)
trans_var = scale_minmax(trans_var)
sns.distplot(trans_var, fit=stats.norm);
plt.title(var + ' Tramsformed')
plt.xlabel('')
plt.subplot(2, 2, 4)
_ = stats.probplot(trans_var, plot=plt)
plt.title('skew=' + '{:.4f}'.format(stats.skew(trans_var)))
plt.xlabel('')
plt.ylabel('')
plt.show()
其中的 skew 指标为与正泰分布的偏差度量值。