二项logistic回归案例分附操作析（数据）

当因变量数据类型为分类变量时，线性回归不再适用，应当做logistic回归。根据因变量分类水平的不同，具体包括二项logistic回归、多项logistic回归和有序logistic回归。

1.案例背景与分析策略

1.1 案例背景介绍

现收集到银行贷款客户的个人、负债信息，以及曾经是否有过还贷违约的记录，试分析是否违约的相关因素，并构建模型用于贷款违约风险预测。（数据来源：SPSS自带案例数据集）

数据上传SPSSAU后，在 “我的数据”中查看浏览原始数据，前5行数据如下：

图1 “我的数据”查看浏览数据集

1.2 明确目的与分析策略

通过SPSSAU“数据处理”栏目下的【数据标签】功能，可以直观观察变量数据类型，显然，“违约”、“教育水平”为分类数据，其他为连续型数据。其中本案例关注的目标变量“违约”数据为两种结局的二分类数据。具体见下图。

图2 SPSSAU的【数据标签】界面

欲研究“是否违约”与哪些因素有关，或哪些变量对“是否违约”有预测作用，考虑以“是否违约”为因变量，其他潜在的因素作为自变量进行回归分析。

由于“是否违约”为二分类变量，因此选用构建二项logistic回归模型。既可以考察影响因素，也可以用于风险预测。

2.数据预处理

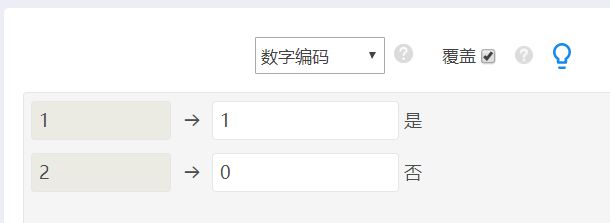
SPSSAU做二项logistic回归，要求因变量须是“0-1”数据编码。

2.1 因变量重新数据编码

打开“数据处理”栏目下的【数据编码】，按图3所示的操作，将数据重新编码，原来的数字编码1表示违约“是”，保持不变，而将原来的编码2修改为0，表示未违约“否”。

图3 SPSSAU的【数据编码】操作

2.2 分类自变量哑变量转换

Logistic回归的自变量，可以是连续型数据也可以是分类型数据。对于分类型自变量，应酌情考虑先以哑变量形式进行回归分析。

本案例中，拟对“受教育水平”进行哑变量处理，以第一个水平作为参照水平。

打开“数据处理”栏目下的【数据编码】，选中“教育水平”，然后在生存变量框里面选择【虚拟哑变量】，点“确认处理”，此时原始数据中会新增加5个“0-1”编码的虚拟变量。具体操作见图4。

图4 SPSSAU的【生成变量】操作

3.单因素分析

为尽可能了解单个因素对“是否违约”的影响，同时防止在多因素分析时遗漏某些重要因素，在探索性分析目的下，可以先就单个因素的预测作用进行分析（非必须步骤）。

根据因变量、自变量的数据类型不同，可以考虑进行交叉表卡方检验、单因素方差分析（t检验）或单因素的logistic回归。

3.1 针对分类自变量的卡方检验

针对“教育水平”分类数据，以交叉表卡方检验考量其与“是否违约”的关系。

打开“通用方法”栏目下的【交叉卡方】，将“违约”拖拽之【定类X】，将“教育水平”拖拽至【定类Y】。

SPSSAU直接输出的是科研论文三线表，可以直接解读和使用。

图5 交叉表卡方检验结果

由上表可知，不同的学历客户的违约率差异有统计学意义（χ²=11.49，P=0.02＜0.05）。

3.2 针对连续自变量的t检验

年龄、工作年、居住年、收入、负债率等其他可能的因素，均为连续型数据。考察他们与“是否违约”的关系，可以采用独立样本t检验或单因素方差分析。

本例使用t检验。打开“通用方法”栏目下的【t检验】，将“违约”拖拽之【定类X】，将年龄、工作年等连续型自变量拖拽至【定量Y】。

图6 独立样本t检验结果

由上表可知，违约及未违约客户的收入差异无统计学意义（t=-1.88，P=0.06＞0.05）。在其他自变量上均值差异有统计学意义（均P值＜0.05）。

实践中，为防止遗漏重要自变量，单因素分析阶段的统计学显著性水平a可适当放宽至0.1甚至0.2。在a=0.1水平下，连续型自变量、分类型自变量与“是否违约”的关联关系均有统计学意义（均P值＜0.1）。

4.多因素logistic回归模型

在单因素分析中有统计学意义的变量（本例为所有自变量）继续进行多因素logistic回归分析。

4.1 逐步回归

打开“进阶方法”栏目下的【二元logistic】，将此前已重新数据编码为“0-1”数据的“是否违约”拖拽至【定量Y】框内，其他变量拖拽至【定量/定类X】框内。

图7 二项logistic回归操作

“教育水平”的5个虚拟变量，本例以第一个水平作为参考，因此是把其他4个“教育水平”虚拟变量作为自变量。具体操作见图7。

因素较多时，可考虑采用逐步回归的方式，由模型自动筛选对因变量有预测作用的自变量构建模型。本案例选择【逐步法】，不勾选【保存残差和预测值】。

4.2 模型拟合评价

首先看模型拟合情况。

图8二元Logit回归模型似然比检验结果

看上表“最终模型”这一行的结果。似然比卡方检验P值＜0.05，说明模型总体上有统计学意义，即至少有一个自变量是有预测作用的。

AIC和BIC值用于多次分析时所得多个模型间的对比，此两值越低越好，实践中，两值更低的模型较优。

模型总体有效后，继续看哪些自变量对因变量的影响是显著的。

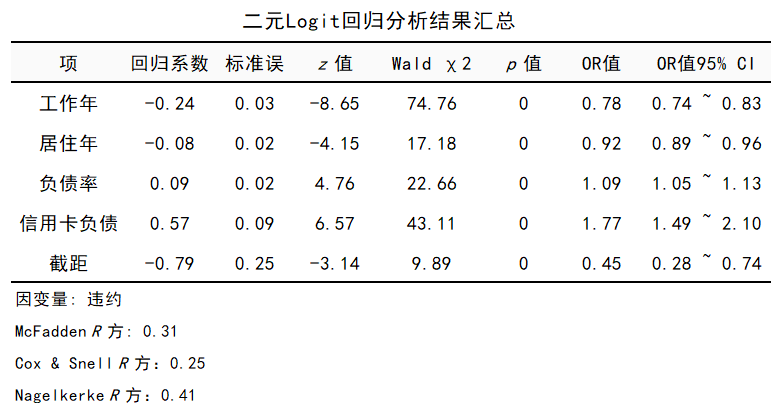
图9二元Logit回归系数表

上表底部的3个R方，类似于线性回归的决定系数R平方，解读方式也类似。大家看SPSSAU智能分析给出的解读：

从上表可以看出，工作年, 居住年, 负债率, 信用卡负债可以解释违约的0.31变化原因。

7个连续型自变量，“教育水平”的4个哑变量（1水平为参照），进入模型及回归系数如上表所示。“工作年”、“居住年”、“负债率”、“信用卡负债”对“是否违约”的影响有统计学意义（均P值＜0.01）。

年龄、收入、其他负债在逐步回归过程中被剔出模型，即他们对“是否违约”的影响无统计学意义。唯一的分类自变量“教育水平”，哑变量均无统计学意义。

“工作年”、“居住年”对“是否违约”有负向预测作用；“负债率”、“信用卡负债”对“是否违约”有正向预测作用。

各自变量影响因变量的方向，建议结合专业经验进行判断，如果发现与专业经验不相符的影响关系，应当重视，重点考察是否存在共线性问题，样本量是否足够等问题。

SPSSAU提供结果智能分析，可以帮助用户快速解读相关结果。比如本例中，对“信用卡负债”对“是否违约”影响的解读：

信用卡负债的回归系数值为0.573，并且呈现出0.01水平的显著性(z=6.566，p=0.000<0.01)，意味着信用卡负债会对违约产生显著的正向影响关系。以及优势比(OR值)为1.774，意味着信用卡负债增加一个单位时，违约的变化(增加)幅度为1.774倍。

智能分析是SPSSAU的优势，对初学者来说会有很大帮助。

对本案例影响因素做个小结：二项logistic回归表明，模型有效，“工作年”、“居住年”、“负债率”、“信用卡负债”是“是否违约”的独立影响因素，前两个具有负向预测作用，后两个具有正向预测作用。

4.3 模型预测能力

回归分析除了影响因素分析外，还可以实现预测。在本例中，我们的目的之一就是要预测贷款违约风险。

SPSSAU的智能分析可以直接写出logistic回归表达式，本例如下：

ln(p/1-p)=-0.791-0.243*工作年-0.081*居住年 + 0.088*负债率 + 0.573*信用卡负债

(其中p代表违约为1 的概率，1-p代表违约为0的概率)。

根据该表达式，我们代入新的客户数据，即可预测该客户违约风险。注意，如果所得P值＞0.5（SPSSAU默认的预测0或1的界值）则预测为“违约=1”，反之预测为“违约=0”。

图10 SPSSAU的模型预测功能

SPSSAU提供了“模型预测”功能，代入新数据即可实现单个个案的风险预测。

假设某客户工作年16、居住年13、负债率10.9、信用卡负债0.54，具体见图10。模型预测概率P=0.011＜0.5，预测该客户“违约=1”的概率为0.011，反过来预测其“违约=0”概率为1-0.011=0.989，即该客户未来会违约是低风险事件。

我们构建的二项logistic回归模型，它的预测能力到底如何呢？SPSSAU基于训练集数据，对预测准确率进行回归，提供下表：

图11 二项logistic回归模型预测准确率评价

由上表可知，模型预测“违约=0”的准确率为92.46%，预测“违约=1”的准确率为50.27%，总体准确率为81.43%。

实践中，我们更关注预测“违约=1”的准确率，就本例而言，银行放贷更关注未来发生违约的风险。本例50.27的准确率，是偏低的。

所以，本例所构建的模型仍然有待进一步研究以提升其预测能力。

5.小结

二项logistic回归对样本量有一定要求，一般经验认为（0-1结局）结局为1的样本量应是自变量个数的10~20倍。

此外还需要重视自变量间多重共线性的影响，异常数据的影响。

PS：案例数据如下：

案例数据​spssau.com/spssaudata.html?shareData=7C05BE9262CE