pytorch-optimizer--优化算法
函数
1.zero_grad()
将梯度清零。由于 PyTorch 不会自动清零梯度,所以在每一次更新前会进行此操作。
2. state_dict()
获取模型当前的参数,以一个有序字典形式返回。
这个有序字典中,key 是各层参数名,value 就是参数。
3. load_state_dict(state_dict)
将 state_dict 中的参数加载到当前网络,常用于 finetune。
4.add_param_group()
给 optimizer 管理的参数组中增加一组参数,可为该组参数定制 lr, momentum, weight_decay 等
5.step(closure)
执行一步权值更新, 其中可传入参数 closure(一个闭包)。如,当采用 LBFGS优化方法时,需要多次计算,因此需要传入一个闭包去允许它们重新计算 loss
SGD
http://www.cs.toronto.edu/%7Ehinton/absps/momentum.pdf
使用Momentum/Nesterov实现SGD与Sutskever等人和其他一些框架中的实现有细微的不同
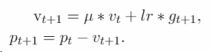
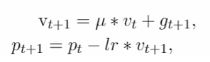
缺点:
有可能会陷入局部最小值;
不会收敛,最终会一直在最小值附近波动,并不会达到最小值并停留在此;
下降速度慢;
选择合适的learning rate比较困难;
在所有方向上统一的缩放梯度,不适用于稀疏数据
"""
optimizer.SGD
torch.optimizer.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
随机梯度下降法
主要参数:
lr (float) – 学习率
momentum (float, 可选) – 动量因子(默认:0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认:0)
dampening (float, 可选) – 动量的抑制因子(默认:0)
nesterov (bool, 可选) – 使用Nesterov动量(默认:False)
"""
class SGD(Optimizer):
def __init__(self, params, lr=required, momentum=0, dampening=0,weight_decay=0, nesterov=False):
defaults = dict(lr=lr, momentum=momentum, dampening=dampening,weight_decay=weight_decay,nesterov=nesterov)
if nesterov and (momentum <= 0 or dampening != 0):
raise ValueError("Nesterov momentum requires a momentum and zero dampening")
super(SGD, self).__init__(params, defaults)
def __setstate__(self, state):
super(SGD, self).__setstate__(state)
for group in self.param_groups:
#如果键不存在于字典中,将会添加键并将值设为默认值。
group.setdefault('nesterov', False)
# 没有torch.no_grad(),导致模型运算的时候不能释放显存(记录了梯度信息),所以显存大
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups: # 本组参数更新所必需的参数设置
weight_decay = group['weight_decay'] #动量因子(默认:0)
momentum = group['momentum'] #权重衰减(L2惩罚)(默认:0)
dampening = group['dampening'] #动量的抑制因子(默认:0)
nesterov = group['nesterov'] #使用Nesterov动量(默认:False)
# p即为待更新的参数矩阵(权重/bias);d_p为.backward()方法计算出的loss对参数的梯度矩阵
for p in group['params']:
if p.grad is None: # 如果没有梯度,则直接下一步
continue
d_p = p.grad
# 正则化及动量累积操作
# 等价于d_p = d_p + p × dacay
if weight_decay != 0:
# 防止过拟合的参数,样本越多,该值越小,模型参数越多,该值越大,
# L2正则化的目的就是为了让权重衰减到更小的值,在一定程度上减少模型过拟合的问题,所以权重衰减也叫L2正则化。
d_p = d_p.add(p, alpha=weight_decay)
if momentum != 0:
param_state = self.state[p]
if 'momentum_buffer' not in param_state:
buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
# detach()函数可以返回一个完全相同的tensor, 与旧tensor共享内存,脱离计算图,不牵扯梯度计算。
else:
buf = param_state['momentum_buffer']
buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
if nesterov:
d_p = d_p.add(buf, alpha=momentum)
else:
d_p = buf
# 当前组学习参数更新
# p = p - lr×d_p
p.add_(d_p, alpha=-group['lr'])
return loss
ASGD
ASGD 也成为 SAG,均表示随机平均梯度下降(Averaged Stochastic Gradient Descent),简单地说 ASGD 就是用空间换时间的一种 SGD
https://dl.acm.org/citation.cfm?id=131098
"""
optimizer.ASGD
torch.optimizer.ASGD(params,lr=0.01,lambd=0.0001,alpha=0.75, t0=1000000.0, weight_decay=0)
随机平均梯度下降
主要参数
lr (float, 可选) – 学习率(默认:1e-2)
lambd (float, 可选) – 衰减项(默认:1e-4)
alpha (float, 可选) – eta更新的指数(默认:0.75)
t0 (float, 可选) – 指明在哪一次开始平均化(默认:1e-6)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
"""
class ASGD(Optimizer):
def __init__(self, params, lr=1e-2, lambd=1e-4, alpha=0.75, t0=1e6, weight_decay=0):
defaults = dict(lr=lr, lambd=lambd, alpha=alpha, t0=t0,weight_decay=weight_decay)
super(ASGD, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if grad.is_sparse:
# ASGD不支持稀疏渐变
raise RuntimeError('ASGD does not support sparse gradients')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
state['eta'] = group['lr']
state['mu'] = 1
state['ax'] = torch.zeros_like(p, memory_format=torch.preserve_format)
state['step'] += 1
if group['weight_decay'] != 0:
grad = grad.add(p, alpha=group['weight_decay'])
# decay term 衰变项
p.mul_(1 - group['lambd'] * state['eta'])
# update parameter
p.add_(grad, alpha=-state['eta'])
# averaging
if state['mu'] != 1:
state['ax'].add_(p.sub(state['ax']).mul(state['mu']))
else:
state['ax'].copy_(p)
# update eta and mu
state['eta'] = (group['lr'] / math.pow((1 + group['lambd'] * group['lr'] * state['step']), group['alpha']))
state['mu'] = 1 / max(1, state['step'] - group['t0'])
return loss
Adagrad
实现 Adagrad 优化方法(Adaptive Gradient),Adagrad 是一种自适应优化方法,是自适应的为各个参数分配不同的学习率。这个学习率的变化,会受到梯度的大小和迭代次数的影响。梯度越大,学习率越小;梯度越小,学习率越大。缺点是训练后期,学习率过小,因为 Adagrad 累加之前所有的梯度平方作为分母。
Adaptive Subgradient Methods for Online Learning and Stochastic
Optimization: http://jmlr.org/papers/v12/duchi11a.html
"""
optimizer.Adagrad
torch.optimizer.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)
自适应学习率下降法
主要参数:
lr (float, 可选) – 学习率(默认: 1e-2)
lr_decay (float, 可选) – 学习率衰减(默认: 0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
"""
class Adagrad(Optimizer):
def __init__(self, params, lr=1e-2, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10):
defaults = dict(lr=lr, lr_decay=lr_decay, eps=eps, weight_decay=weight_decay,initial_accumulator_value=initial_accumulator_value)
super(Adagrad, self).__init__(params, defaults)
for group in self.param_groups:
for p in group['params']:
state = self.state[p]
state['step'] = 0
#torch.full_like()就是将input的形状作为返回结果tensor的形状
state['sum'] = torch.full_like(p, initial_accumulator_value, memory_format=torch.preserve_format)
def share_memory(self):
for group in self.param_groups:
for p in group['params']:
state = self.state[p]
state['sum'].share_memory_()
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
params_with_grad = []
grads = []
state_sums = []
state_steps = []
for p in group['params']:
if p.grad is not None:
params_with_grad.append(p)
grads.append(p.grad)
state = self.state[p]
# append() 方法在被选元素的结尾(仍然在内部)插入指定内容
state_sums.append(state['sum'])
# update the steps for each param group update 更新每个参数组更新的步骤
state['step'] += 1
# record the step after step update 记录一步接一步的更新
state_steps.append(state['step'])
F.adagrad(params_with_grad,
grads,
state_sums,
state_steps,
group['lr'],
group['weight_decay'],
group['lr_decay'],
group['eps'])
return loss
Adadelta
实现 Adadelta 优化方法。Adadelta 是 Adagrad 的改进。Adadelta 分母中采用距离当前时间点比较近的累计项,这可以避免在训练后期,学习率过小。
https://arxiv.org/abs/1212.5701
"""
optimizer.Adadelta
torch.optimizer.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
主要参数:
rho (float, 可选) – 用于计算平方梯度的运行平均值的系数(默认:0.9)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-6)
lr (float, 可选) – 在delta被应用到参数更新之前对它缩放的系数(默认:1.0)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
"""
class Adadelta(Optimizer):
def __init__(self, params, lr=1.0, rho=0.9, eps=1e-6, weight_decay=0):
defaults = dict(lr=lr, rho=rho, eps=eps, weight_decay=weight_decay)
super(Adadelta, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if grad.is_sparse:
raise RuntimeError('Adadelta does not support sparse gradients')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
state['square_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
state['acc_delta'] = torch.zeros_like(p, memory_format=torch.preserve_format)
square_avg, acc_delta = state['square_avg'], state['acc_delta']
rho, eps = group['rho'], group['eps']
state['step'] += 1
if group['weight_decay'] != 0:
grad = grad.add(p, alpha=group['weight_decay'])
#addcmul_()执行tensor1由tensor2对元素的乘法,将结果乘以标量值并将其添加到输入中。
square_avg.mul_(rho).addcmul_(grad, grad, value=1 - rho)
std = square_avg.add(eps).sqrt_()
delta = acc_delta.add(eps).sqrt_().div_(std).mul_(grad)
p.add_(delta, alpha=-group['lr'])
acc_delta.mul_(rho).addcmul_(delta, delta, value=1 - rho)
return loss
Adamax
实现 Adamax 优化方法。Adamax 是对 Adam 增加了一个学习率上限的概念,所以也称之为 Adamax。
https://arxiv.org/abs/1412.6980
"""
optimizer.Adamax
torch.optimizer.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
Adam增加学习率上限
主要参数:
lr (float, 可选) – 学习率(默认:2e-3)
betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
"""
class Adamax(Optimizer):
def __init__(self, params, lr=2e-3, betas=(0.9, 0.999), eps=1e-8,weight_decay=0):
defaults = dict(lr=lr, betas=betas, eps=eps, weight_decay=weight_decay)
super(Adamax, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if grad.is_sparse:
raise RuntimeError('Adamax does not support sparse gradients')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
state['exp_inf'] = torch.zeros_like(p, memory_format=torch.preserve_format)
exp_avg, exp_inf = state['exp_avg'], state['exp_inf']
beta1, beta2 = group['betas']
eps = group['eps']
state['step'] += 1
if group['weight_decay'] != 0:
grad = grad.add(p, alpha=group['weight_decay'])
# Update biased first moment estimate.
exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
# Update the exponentially weighted infinity norm.
norm_buf = torch.cat([
exp_inf.mul_(beta2).unsqueeze(0),
grad.abs().add_(eps).unsqueeze_(0)
], 0)
torch.amax(norm_buf, 0, keepdim=False, out=exp_inf)
bias_correction = 1 - beta1 ** state['step']
clr = group['lr'] / bias_correction
p.addcdiv_(exp_avg, exp_inf, value=-clr)
return loss
lbfgs
实现 L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)优化方法。L-BFGS 属于拟牛顿算法。L-BFGS 是对 BFGS 的改进,特点就是节省内存
"""
optimizer.LBFGS
torch.optimizer.LBFGS(params,lr=1,max_iter=20,max_eval=None,tolerance_grad=1e-05,tolerance_change=1e-09, history_size=100, line_search_fn=None)
一种BFGS的改进
主要参数:
lr (float) – 学习率(默认:1)
max_iter (int) – 每一步优化的最大迭代次数(默认:20))
max_eval (int) – 每一步优化的最大函数评价次数(默认:max * 1.25)
tolerance_grad (float) – 一阶最优的终止容忍度(默认:1e-5)
tolerance_change (float) – 在函数值/参数变化量上的终止容忍度(默认:1e-9)
history_size (int) – 更新历史的大小(默认:100)
"""
def _cubic_interpolate(x1, f1, g1, x2, f2, g2, bounds=None):
# ported from https://github.com/torch/optim/blob/master/polyinterp.lua
# Compute bounds of interpolation area
if bounds is not None:
xmin_bound, xmax_bound = bounds
else:
xmin_bound, xmax_bound = (x1, x2) if x1 <= x2 else (x2, x1)
# Code for most common case: cubic interpolation of 2 points
# w/ function and derivative values for both
# Solution in this case (where x2 is the farthest point):
# d1 = g1 + g2 - 3*(f1-f2)/(x1-x2);
# d2 = sqrt(d1^2 - g1*g2);
# min_pos = x2 - (x2 - x1)*((g2 + d2 - d1)/(g2 - g1 + 2*d2));
# t_new = min(max(min_pos,xmin_bound),xmax_bound);
d1 = g1 + g2 - 3 * (f1 - f2) / (x1 - x2)
d2_square = d1**2 - g1 * g2
if d2_square >= 0:
d2 = d2_square.sqrt()
if x1 <= x2:
min_pos = x2 - (x2 - x1) * ((g2 + d2 - d1) / (g2 - g1 + 2 * d2))
else:
min_pos = x1 - (x1 - x2) * ((g1 + d2 - d1) / (g1 - g2 + 2 * d2))
return min(max(min_pos, xmin_bound), xmax_bound)
else:
return (xmin_bound + xmax_bound) / 2.
def _strong_wolfe(obj_func,
x,
t,
d,
f,
g,
gtd,
c1=1e-4,
c2=0.9,
tolerance_change=1e-9,
max_ls=25):
# ported from https://github.com/torch/optim/blob/master/lswolfe.lua
d_norm = d.abs().max()
g = g.clone(memory_format=torch.contiguous_format)
# evaluate objective and gradient using initial step
f_new, g_new = obj_func(x, t, d)
ls_func_evals = 1
gtd_new = g_new.dot(d)
# bracket an interval containing a point satisfying the Wolfe criteria
t_prev, f_prev, g_prev, gtd_prev = 0, f, g, gtd
done = False
ls_iter = 0
while ls_iter < max_ls:
# check conditions
if f_new > (f + c1 * t * gtd) or (ls_iter > 1 and f_new >= f_prev):
bracket = [t_prev, t]
bracket_f = [f_prev, f_new]
bracket_g = [g_prev, g_new.clone(memory_format=torch.contiguous_format)]
bracket_gtd = [gtd_prev, gtd_new]
break
if abs(gtd_new) <= -c2 * gtd:
bracket = [t]
bracket_f = [f_new]
bracket_g = [g_new]
done = True
break
if gtd_new >= 0:
bracket = [t_prev, t]
bracket_f = [f_prev, f_new]
bracket_g = [g_prev, g_new.clone(memory_format=torch.contiguous_format)]
bracket_gtd = [gtd_prev, gtd_new]
break
# interpolate
min_step = t + 0.01 * (t - t_prev)
max_step = t * 10
tmp = t
t = _cubic_interpolate(
t_prev,
f_prev,
gtd_prev,
t,
f_new,
gtd_new,
bounds=(min_step, max_step))
# next step
t_prev = tmp
f_prev = f_new
g_prev = g_new.clone(memory_format=torch.contiguous_format)
gtd_prev = gtd_new
f_new, g_new = obj_func(x, t, d)
ls_func_evals += 1
gtd_new = g_new.dot(d)
ls_iter += 1
# reached max number of iterations?
if ls_iter == max_ls:
bracket = [0, t]
bracket_f = [f, f_new]
bracket_g = [g, g_new]
# zoom phase: we now have a point satisfying the criteria, or
# a bracket around it. We refine the bracket until we find the
# exact point satisfying the criteria
insuf_progress = False
# find high and low points in bracket
low_pos, high_pos = (0, 1) if bracket_f[0] <= bracket_f[-1] else (1, 0)
while not done and ls_iter < max_ls:
# line-search bracket is so small
if abs(bracket[1] - bracket[0]) * d_norm < tolerance_change:
break
# compute new trial value
t = _cubic_interpolate(bracket[0], bracket_f[0], bracket_gtd[0],
bracket[1], bracket_f[1], bracket_gtd[1])
# test that we are making sufficient progress:
# in case `t` is so close to boundary, we mark that we are making
# insufficient progress, and if
# + we have made insufficient progress in the last step, or
# + `t` is at one of the boundary,
# we will move `t` to a position which is `0.1 * len(bracket)`
# away from the nearest boundary point.
eps = 0.1 * (max(bracket) - min(bracket))
if min(max(bracket) - t, t - min(bracket)) < eps:
# interpolation close to boundary
if insuf_progress or t >= max(bracket) or t <= min(bracket):
# evaluate at 0.1 away from boundary
if abs(t - max(bracket)) < abs(t - min(bracket)):
t = max(bracket) - eps
else:
t = min(bracket) + eps
insuf_progress = False
else:
insuf_progress = True
else:
insuf_progress = False
# Evaluate new point 评估新点
f_new, g_new = obj_func(x, t, d)
ls_func_evals += 1
gtd_new = g_new.dot(d)
ls_iter += 1
if f_new > (f + c1 * t * gtd) or f_new >= bracket_f[low_pos]:
# Armijo condition not satisfied or not lower than lowest point
bracket[high_pos] = t
bracket_f[high_pos] = f_new
bracket_g[high_pos] = g_new.clone(memory_format=torch.contiguous_format)
bracket_gtd[high_pos] = gtd_new
low_pos, high_pos = (0, 1) if bracket_f[0] <= bracket_f[1] else (1, 0)
else:
if abs(gtd_new) <= -c2 * gtd:
# Wolfe conditions satisfied
done = True
elif gtd_new * (bracket[high_pos] - bracket[low_pos]) >= 0:
# old high becomes new low
bracket[high_pos] = bracket[low_pos]
bracket_f[high_pos] = bracket_f[low_pos]
bracket_g[high_pos] = bracket_g[low_pos]
bracket_gtd[high_pos] = bracket_gtd[low_pos]
# new point becomes new low 新点变新低
bracket[low_pos] = t
bracket_f[low_pos] = f_new
bracket_g[low_pos] = g_new.clone(memory_format=torch.contiguous_format)
bracket_gtd[low_pos] = gtd_new
# return stuff
t = bracket[low_pos]
f_new = bracket_f[low_pos]
g_new = bracket_g[low_pos]
return f_new, g_new, t, ls_func_evals
class LBFGS(Optimizer):
"""Implements L-BFGS algorithm, heavily inspired by `minFunc
<https://www.cs.ubc.ca/~schmidtm/Software/minFunc.html>`.
.. warning::
This optimizer doesn't support per-parameter options and parameter
groups (there can be only one).
.. warning::
Right now all parameters have to be on a single device. This will be
improved in the future.
.. note::
This is a very memory intensive optimizer (it requires additional
``param_bytes * (history_size + 1)`` bytes). If it doesn't fit in memory
try reducing the history size, or use a different algorithm.
Arguments:
lr (float): learning rate (default: 1)
max_iter (int): maximal number of iterations per optimization step
(default: 20)
max_eval (int): maximal number of function evaluations per optimization
step (default: max_iter * 1.25).
tolerance_grad (float): termination tolerance on first order optimality
(default: 1e-5).
tolerance_change (float): termination tolerance on function
value/parameter changes (default: 1e-9).
history_size (int): update history size (default: 100).
line_search_fn (str): either 'strong_wolfe' or None (default: None).
"""
def __init__(self,
params,
lr=1,
max_iter=20,
max_eval=None,
tolerance_grad=1e-7,
tolerance_change=1e-9,
history_size=100,
line_search_fn=None):
if max_eval is None:
max_eval = max_iter * 5 // 4
defaults = dict(
lr=lr,
max_iter=max_iter,
max_eval=max_eval,
tolerance_grad=tolerance_grad,
tolerance_change=tolerance_change,
history_size=history_size,
line_search_fn=line_search_fn)
super(LBFGS, self).__init__(params, defaults)
if len(self.param_groups) != 1:
raise ValueError("LBFGS doesn't support per-parameter options "
"(parameter groups)")
self._params = self.param_groups[0]['params']
self._numel_cache = None
def _numel(self):
if self._numel_cache is None:
self._numel_cache = reduce(lambda total, p: total + p.numel(), self._params, 0)
return self._numel_cache
def _gather_flat_grad(self):
views = []
for p in self._params:
if p.grad is None:
view = p.new(p.numel()).zero_()
elif p.grad.is_sparse:
view = p.grad.to_dense().view(-1)
else:
view = p.grad.view(-1)
views.append(view)
return torch.cat(views, 0)
def _add_grad(self, step_size, update):
offset = 0
for p in self._params:
numel = p.numel()
# view as to avoid deprecated pointwise semantics
p.add_(update[offset:offset + numel].view_as(p), alpha=step_size)
offset += numel
assert offset == self._numel()
def _clone_param(self):
return [p.clone(memory_format=torch.contiguous_format) for p in self._params]
def _set_param(self, params_data):
for p, pdata in zip(self._params, params_data):
p.copy_(pdata)
def _directional_evaluate(self, closure, x, t, d):
self._add_grad(t, d)
loss = float(closure())
flat_grad = self._gather_flat_grad()
self._set_param(x)
return loss, flat_grad
@torch.no_grad()
def step(self, closure):
"""Performs a single optimization step.
Arguments:
closure (callable): A closure that reevaluates the model
and returns the loss.
"""
assert len(self.param_groups) == 1
# Make sure the closure is always called with grad enabled
closure = torch.enable_grad()(closure)
group = self.param_groups[0]
lr = group['lr']
max_iter = group['max_iter']
max_eval = group['max_eval']
tolerance_grad = group['tolerance_grad']
tolerance_change = group['tolerance_change']
line_search_fn = group['line_search_fn']
history_size = group['history_size']
# NOTE: LBFGS has only global state, but we register it as state for
# the first param, because this helps with casting in load_state_dict
state = self.state[self._params[0]]
state.setdefault('func_evals', 0)
state.setdefault('n_iter', 0)
# evaluate initial f(x) and df/dx
orig_loss = closure()
loss = float(orig_loss)
current_evals = 1
state['func_evals'] += 1
flat_grad = self._gather_flat_grad()
opt_cond = flat_grad.abs().max() <= tolerance_grad
# optimal condition
if opt_cond:
return orig_loss
# tensors cached in state (for tracing)
d = state.get('d')
t = state.get('t')
old_dirs = state.get('old_dirs')
old_stps = state.get('old_stps')
ro = state.get('ro')
H_diag = state.get('H_diag')
prev_flat_grad = state.get('prev_flat_grad')
prev_loss = state.get('prev_loss')
n_iter = 0
# optimize for a max of max_iter iterations
while n_iter < max_iter:
# keep track of nb of iterations
n_iter += 1
state['n_iter'] += 1
# compute gradient descent direction
# 计算梯度下降方向
if state['n_iter'] == 1:
d = flat_grad.neg()
old_dirs = []
old_stps = []
ro = []
H_diag = 1
else:
# do lbfgs update (update memory)
y = flat_grad.sub(prev_flat_grad)
s = d.mul(t)
ys = y.dot(s) # y*s
if ys > 1e-10:
# updating memory
if len(old_dirs) == history_size:
# shift history by one (limited-memory)
old_dirs.pop(0)
old_stps.pop(0)
ro.pop(0)
# store new direction/step
old_dirs.append(y)
old_stps.append(s)
ro.append(1. / ys)
# update scale of initial Hessian approximation
H_diag = ys / y.dot(y) # (y*y)
# compute the approximate (L-BFGS) inverse Hessian
# multiplied by the gradient
num_old = len(old_dirs)
if 'al' not in state:
state['al'] = [None] * history_size
al = state['al']
# iteration in L-BFGS loop collapsed to use just one buffer
q = flat_grad.neg()
for i in range(num_old - 1, -1, -1):
al[i] = old_stps[i].dot(q) * ro[i]
q.add_(old_dirs[i], alpha=-al[i])
# multiply by initial Hessian
# r/d is the final direction
d = r = torch.mul(q, H_diag)
for i in range(num_old):
be_i = old_dirs[i].dot(r) * ro[i]
r.add_(old_stps[i], alpha=al[i] - be_i)
if prev_flat_grad is None:
prev_flat_grad = flat_grad.clone(memory_format=torch.contiguous_format)
else:
prev_flat_grad.copy_(flat_grad)
prev_loss = loss
# compute step length 计算步长
# reset initial guess for step size
# 重置步长的初始猜测
if state['n_iter'] == 1:
t = min(1., 1. / flat_grad.abs().sum()) * lr
else:
t = lr
# directional derivative
gtd = flat_grad.dot(d) # g * d
# directional derivative is below tolerance
if gtd > -tolerance_change:
break
# optional line search: user function
ls_func_evals = 0
if line_search_fn is not None:
# perform line search, using user function
if line_search_fn != "strong_wolfe":
raise RuntimeError("only 'strong_wolfe' is supported")
else:
x_init = self._clone_param()
def obj_func(x, t, d):
return self._directional_evaluate(closure, x, t, d)
loss, flat_grad, t, ls_func_evals = _strong_wolfe(
obj_func, x_init, t, d, loss, flat_grad, gtd)
self._add_grad(t, d)
opt_cond = flat_grad.abs().max() <= tolerance_grad
else:
# no line search, simply move with fixed-step
self._add_grad(t, d)
if n_iter != max_iter:
# re-evaluate function only if not in last iteration
# the reason we do this: in a stochastic setting,
# no use to re-evaluate that function here
with torch.enable_grad():
loss = float(closure())
flat_grad = self._gather_flat_grad()
opt_cond = flat_grad.abs().max() <= tolerance_grad
ls_func_evals = 1
# update func eval
current_evals += ls_func_evals
state['func_evals'] += ls_func_evals
# check conditions 检查条件
if n_iter == max_iter:
break
if current_evals >= max_eval:
break
# optimal condition
if opt_cond:
break
# lack of progress
if d.mul(t).abs().max() <= tolerance_change:
break
if abs(loss - prev_loss) < tolerance_change:
break
state['d'] = d
state['t'] = t
state['old_dirs'] = old_dirs
state['old_stps'] = old_stps
state['ro'] = ro
state['H_diag'] = H_diag
state['prev_flat_grad'] = prev_flat_grad
state['prev_loss'] = prev_loss
return orig_loss
Adam
实现 Adam(Adaptive Moment Estimation))优化方法。Adam 是一种自适应学习率的优化方法,Adam 利用梯度的一阶矩估计和二阶矩估计动态的调整学习率。Adam 是结合了 Momentum 和 RMSprop,并进行了偏差修正。
_Adam: A Method for Stochastic Optimization:
https://arxiv.org/abs/1412.6980
… _Decoupled Weight Decay Regularization:
https://arxiv.org/abs/1711.05101
… _On the Convergence of Adam and Beyond:
https://openreview.net/forum?id=ryQu7f-RZ
"""
optimizer.Adam
torch.optimizer.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
RMSprop结合Momentum
主要参数:
lr (float, 可选) – 学习率(默认:1e-3)
betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:0.9,0.999)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
"""
class Adam(Optimizer):
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8,weight_decay=0, amsgrad=False):
defaults = dict(lr=lr, betas=betas,eps=eps,weight_decay=weight_decay, amsgrad=amsgrad)
super(Adam, self).__init__(params, defaults)
def __setstate__(self, state):
super(Adam, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('amsgrad', False)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
params_with_grad = []
grads = []
exp_avgs = []
exp_avg_sqs = []
state_sums = []
max_exp_avg_sqs = []
state_steps = []
for p in group['params']:
if p.grad is not None:
params_with_grad.append(p)
if p.grad.is_sparse:
raise RuntimeError('Adam does not support sparse gradients, please consider SparseAdam instead')
grads.append(p.grad)
state = self.state[p]
# Lazy state initialization
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
# Exponential moving average of squared gradient values
state['exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)
if group['amsgrad']:
# Maintains max of all exp. moving avg. of sq. grad. values
state['max_exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)
exp_avgs.append(state['exp_avg'])
exp_avg_sqs.append(state['exp_avg_sq'])
if group['amsgrad']:
max_exp_avg_sqs.append(state['max_exp_avg_sq'])
# update the steps for each param group update
state['step'] += 1
# record the step after step update
state_steps.append(state['step'])
beta1, beta2 = group['betas']
F.adam(params_with_grad,
grads,
exp_avgs,
exp_avg_sqs,
max_exp_avg_sqs,
state_steps,
group['amsgrad'],
beta1,
beta2,
group['lr'],
group['weight_decay'],
group['eps']
)
return loss
RAdam
"""
optimizer.RAdam
torch.optimizer.RAdam(params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=0, degenerated_to_sgd=True)
随机梯度下降法
主要参数:
lr (float) – 学习率
betas (Tuple[float, float], 可选) – 计算梯度及其平方的运行平均值的系数(默认值:(0.9,0.999))
eps (float, 可选) – 为提高数值稳定性而增加的分母项(默认值: 1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认:0)
degenerated_to_sgd(boolean, 可选)
"""
class RAdam(Optimizer):
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=0, degenerated_to_sgd=True):
if not 0.0 <= lr:
raise ValueError("Invalid learning rate: {}".format(lr))
if not 0.0 <= eps:
raise ValueError("Invalid epsilon value: {}".format(eps))
if not 0.0 <= betas[0] < 1.0:
raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
if not 0.0 <= betas[1] < 1.0:
raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
self.degenerated_to_sgd = degenerated_to_sgd
if isinstance(params, (list, tuple)) and len(params) > 0 and isinstance(params[0], dict):
for param in params:
if 'betas' in param and (param['betas'][0] != betas[0] or param['betas'][1] != betas[1]):
param['buffer'] = [[None, None, None] for _ in range(10)]
defaults = dict(lr=lr, betas=betas, eps=eps, weight_decay=weight_decay, buffer=[[None, None, None] for _ in range(10)])
super(RAdam, self).__init__(params, defaults)
def __setstate__(self, state):
super(RAdam, self).__setstate__(state)
def step(self, closure=None):
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data.float()
if grad.is_sparse:
raise RuntimeError('RAdam does not support sparse gradients')
p_data_fp32 = p.data.float()
state = self.state[p]
if len(state) == 0:
state['step'] = 0
state['exp_avg'] = torch.zeros_like(p_data_fp32)
state['exp_avg_sq'] = torch.zeros_like(p_data_fp32)
else:
state['exp_avg'] = state['exp_avg'].type_as(p_data_fp32)
state['exp_avg_sq'] = state['exp_avg_sq'].type_as(p_data_fp32)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
beta1, beta2 = group['betas']
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)
exp_avg.mul_(beta1).add_(1 - beta1, grad)
state['step'] += 1
buffered = group['buffer'][int(state['step'] % 10)]
if state['step'] == buffered[0]:
N_sma, step_size = buffered[1], buffered[2]
else:
buffered[0] = state['step']
beta2_t = beta2 ** state['step']
N_sma_max = 2 / (1 - beta2) - 1
N_sma = N_sma_max - 2 * state['step'] * beta2_t / (1 - beta2_t)
buffered[1] = N_sma
# more conservative since it's an approximated value
if N_sma >= 5:
step_size = math.sqrt((1 - beta2_t) * (N_sma - 4) / (N_sma_max - 4) * (N_sma - 2) / N_sma * N_sma_max / (N_sma_max - 2)) / (1 - beta1 ** state['step'])
elif self.degenerated_to_sgd:
step_size = 1.0 / (1 - beta1 ** state['step'])
else:
step_size = -1
buffered[2] = step_size
# more conservative since it's an approximated value 更保守,因为它是一个近似值
if N_sma >= 5:
if group['weight_decay'] != 0:
p_data_fp32.add_(-group['weight_decay'] * group['lr'], p_data_fp32)
denom = exp_avg_sq.sqrt().add_(group['eps'])
p_data_fp32.addcdiv_(-step_size * group['lr'], exp_avg, denom)
p.data.copy_(p_data_fp32)
elif step_size > 0:
if group['weight_decay'] != 0:
p_data_fp32.add_(-group['weight_decay'] * group['lr'], p_data_fp32)
p_data_fp32.add_(-step_size * group['lr'], exp_avg)
p.data.copy_(p_data_fp32)
return loss
class PlainRAdam(Optimizer):
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=0, degenerated_to_sgd=True):
if not 0.0 <= lr:
raise ValueError("Invalid learning rate: {}".format(lr))
if not 0.0 <= eps:
raise ValueError("Invalid epsilon value: {}".format(eps))
if not 0.0 <= betas[0] < 1.0:
raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
if not 0.0 <= betas[1] < 1.0:
raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
#索引1处的beta参数无效:{}
self.degenerated_to_sgd = degenerated_to_sgd
defaults = dict(lr=lr, betas=betas, eps=eps, weight_decay=weight_decay)
super(PlainRAdam, self).__init__(params, defaults)
def __setstate__(self, state):
super(PlainRAdam, self).__setstate__(state)
def step(self, closure=None):
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data.float()
if grad.is_sparse:
raise RuntimeError('RAdam does not support sparse gradients')
p_data_fp32 = p.data.float()
state = self.state[p]
if len(state) == 0:
state['step'] = 0
state['exp_avg'] = torch.zeros_like(p_data_fp32)
state['exp_avg_sq'] = torch.zeros_like(p_data_fp32)
else:
state['exp_avg'] = state['exp_avg'].type_as(p_data_fp32)
state['exp_avg_sq'] = state['exp_avg_sq'].type_as(p_data_fp32)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
beta1, beta2 = group['betas']
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)
exp_avg.mul_(beta1).add_(1 - beta1, grad)
state['step'] += 1
beta2_t = beta2 ** state['step']
N_sma_max = 2 / (1 - beta2) - 1
N_sma = N_sma_max - 2 * state['step'] * beta2_t / (1 - beta2_t)
# more conservative since it's an approximated value
if N_sma >= 5:
if group['weight_decay'] != 0:
p_data_fp32.add_(-group['weight_decay'] * group['lr'], p_data_fp32)
step_size = group['lr'] * math.sqrt((1 - beta2_t) * (N_sma - 4) / (N_sma_max - 4) * (N_sma - 2) / N_sma * N_sma_max / (N_sma_max - 2)) / (1 - beta1 ** state['step'])
denom = exp_avg_sq.sqrt().add_(group['eps'])
p_data_fp32.addcdiv_(-step_size, exp_avg, denom)
p.data.copy_(p_data_fp32)
elif self.degenerated_to_sgd:
if group['weight_decay'] != 0:
p_data_fp32.add_(-group['weight_decay'] * group['lr'], p_data_fp32)
step_size = group['lr'] / (1 - beta1 ** state['step'])
p_data_fp32.add_(-step_size, exp_avg)
p.data.copy_(p_data_fp32)
return loss
class AdamW(Optimizer):
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=0, warmup = 0):
if not 0.0 <= lr:
raise ValueError("Invalid learning rate: {}".format(lr))
if not 0.0 <= eps:
raise ValueError("Invalid epsilon value: {}".format(eps))
if not 0.0 <= betas[0] < 1.0:
raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
if not 0.0 <= betas[1] < 1.0:
raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
defaults = dict(lr=lr, betas=betas, eps=eps,
weight_decay=weight_decay, warmup = warmup)
super(AdamW, self).__init__(params, defaults)
def __setstate__(self, state):
super(AdamW, self).__setstate__(state)
def step(self, closure=None):
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data.float()
if grad.is_sparse:
raise RuntimeError('Adam does not support sparse gradients, please consider SparseAdam instead')
p_data_fp32 = p.data.float()
state = self.state[p]
if len(state) == 0:
state['step'] = 0
state['exp_avg'] = torch.zeros_like(p_data_fp32)
state['exp_avg_sq'] = torch.zeros_like(p_data_fp32)
else:
state['exp_avg'] = state['exp_avg'].type_as(p_data_fp32)
state['exp_avg_sq'] = state['exp_avg_sq'].type_as(p_data_fp32)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
beta1, beta2 = group['betas']
state['step'] += 1
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)
exp_avg.mul_(beta1).add_(1 - beta1, grad)
denom = exp_avg_sq.sqrt().add_(group['eps'])
bias_correction1 = 1 - beta1 ** state['step']
bias_correction2 = 1 - beta2 ** state['step']
if group['warmup'] > state['step']:
scheduled_lr = 1e-8 + state['step'] * group['lr'] / group['warmup']
else:
scheduled_lr = group['lr']
step_size = scheduled_lr * math.sqrt(bias_correction2) / bias_correction1
if group['weight_decay'] != 0:
p_data_fp32.add_(-group['weight_decay'] * scheduled_lr, p_data_fp32)
p_data_fp32.addcdiv_(-step_size, exp_avg, denom)
p.data.copy_(p_data_fp32)
return loss
AdaBound
"""
optimizer.AdaBound
torch.optimizer.AdaBound(params, lr=,betas=(0.9,0.999),final_lr=, gamma=1e-3 ,eps=1e-8 , weight_decay=0, amsbound=False)
随机梯度下降法
主要参数:
lr (float) – 学习率
betas (Tuple[float, float], 可选) – 计算梯度及其平方的运行平均值的系数(默认值:(0.9,0.999))
final_lr (float, 可选) – 最终(SGD)学习率
gamma (float, 可选) – 有界函数的收敛速度(默认值:1e-3)
eps (float, 可选) – 为提高数值稳定性而增加的分母项(默认值: 1e-8)
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认:0)
amsbound (boolean, 可选) – 是否使用此算法的AMSBound变量
"""
class AdaBound(Optimizer):
"""Implements AdaBound algorithm.
It has been proposed in `Adaptive Gradient Methods with Dynamic Bound of Learning Rate`_.
Arguments:
params (iterable): iterable of parameters to optimize or dicts defining
parameter groups
lr (float, optional): Adam learning rate (default: 1e-3)
betas (Tuple[float, float], optional): coefficients used for computing
running averages of gradient and its square (default: (0.9, 0.999))
用于计算梯度及其平方的运行平均值的系数(默认值:(0.9,0.999))
final_lr (float, optional): final (SGD) learning rate (default: 0.1)
gamma (float, optional): convergence speed of the bound functions (default: 1e-3)
有界函数的收敛速度(默认值:1e-3)
eps (float, optional): term added to the denominator to improve numerical stability (default: 1e-8)
为提高数值稳定性而增加的分母项
weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
amsbound (boolean, optional): whether to use the AMSBound variant of this algorithm
是否使用此算法的AMSBound变量
.. Adaptive Gradient Methods with Dynamic Bound of Learning Rate: 具有学习率动态界的自适应梯度方法
https://openreview.net/forum?id=Bkg3g2R9FX
"""
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), final_lr=0.1, gamma=1e-3,
eps=1e-8, weight_decay=0, amsbound=False):
if not 0.0 <= lr:
raise ValueError("Invalid learning rate: {}".format(lr))
if not 0.0 <= eps:
raise ValueError("Invalid epsilon value: {}".format(eps))
if not 0.0 <= betas[0] < 1.0:
raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
if not 0.0 <= betas[1] < 1.0:
raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
if not 0.0 <= final_lr:
raise ValueError("Invalid final learning rate: {}".format(final_lr))
if not 0.0 <= gamma < 1.0:
raise ValueError("Invalid gamma parameter: {}".format(gamma))
defaults = dict(lr=lr, betas=betas, final_lr=final_lr, gamma=gamma, eps=eps,
weight_decay=weight_decay, amsbound=amsbound)
super(AdaBound, self).__init__(params, defaults)
self.base_lrs = list(map(lambda group: group['lr'], self.param_groups))
def __setstate__(self, state):
super(AdaBound, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('amsbound', False)
def step(self, closure=None):
"""Performs a single optimization step.
Arguments:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
loss = None
if closure is not None:
loss = closure()
for group, base_lr in zip(self.param_groups, self.base_lrs):
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data
if grad.is_sparse:
raise RuntimeError(
'Adam does not support sparse gradients, please consider SparseAdam instead')
amsbound = group['amsbound']
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values 梯度值的指数移动平均
state['exp_avg'] = torch.zeros_like(p.data)
# Exponential moving average of squared gradient values 平方梯度值的指数移动平均
state['exp_avg_sq'] = torch.zeros_like(p.data)
if amsbound:
# Maintains max of all exp. moving avg. of sq. grad. values
#保持最大的所有实验移动平均平方梯度值
state['max_exp_avg_sq'] = torch.zeros_like(p.data)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
if amsbound:
max_exp_avg_sq = state['max_exp_avg_sq']
beta1, beta2 = group['betas']
state['step'] += 1
if group['weight_decay'] != 0:
grad = grad.add(group['weight_decay'], p.data)
# Decay the first and second moment running average coefficient
#衰减一、二阶矩运行平均系数
exp_avg.mul_(beta1).add_(1 - beta1, grad)
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)
if amsbound:
# Maintains the maximum of all 2nd moment running avg. till now
#到目前为止,保持所有第二时刻运行平均值的最大值
torch.max(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)
# Use the max. for normalizing running avg. of gradient
#使用最大值标准化坡度的运行平均值
denom = max_exp_avg_sq.sqrt().add_(group['eps'])
else:
denom = exp_avg_sq.sqrt().add_(group['eps'])
bias_correction1 = 1 - beta1 ** state['step']
bias_correction2 = 1 - beta2 ** state['step']
step_size = group['lr'] * math.sqrt(bias_correction2) / bias_correction1
# Applies bounds on actual learning rate
# lr_scheduler cannot affect final_lr, this is a workaround to apply lr decay
# 应用实际学习率的界限
# lr调度程序不能影响最终的lr,这是应用lr衰减的一个解决方法
final_lr = group['final_lr'] * group['lr'] / base_lr
lower_bound = final_lr * (1 - 1 / (group['gamma'] * state['step'] + 1))
upper_bound = final_lr * (1 + 1 / (group['gamma'] * state['step']))
step_size = torch.full_like(denom, step_size)
step_size.div_(denom).clamp_(lower_bound, upper_bound).mul_(exp_avg)
p.data.add_(-step_size)
return loss
class AdaBoundW(Optimizer):
"""Implements AdaBound algorithm with Decoupled Weight Decay (arxiv.org/abs/1711.05101)
It has been proposed in `Adaptive Gradient Methods with Dynamic Bound of Learning Rate`_.
Arguments:
params (iterable): iterable of parameters to optimize or dicts defining
parameter groups
lr (float, optional): Adam learning rate (default: 1e-3)
betas (Tuple[float, float], optional): coefficients used for computing
running averages of gradient and its square (default: (0.9, 0.999))
final_lr (float, optional): final (SGD) learning rate (default: 0.1)
gamma (float, optional): convergence speed of the bound functions (default: 1e-3)
eps (float, optional): term added to the denominator to improve
numerical stability (default: 1e-8)
weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
amsbound (boolean, optional): whether to use the AMSBound variant of this algorithm
.. Adaptive Gradient Methods with Dynamic Bound of Learning Rate:
https://openreview.net/forum?id=Bkg3g2R9FX
"""
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), final_lr=0.1, gamma=1e-3,
eps=1e-8, weight_decay=0, amsbound=False):
if not 0.0 <= lr:
raise ValueError("Invalid learning rate: {}".format(lr))
if not 0.0 <= eps:
raise ValueError("Invalid epsilon value: {}".format(eps))
if not 0.0 <= betas[0] < 1.0:
raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
if not 0.0 <= betas[1] < 1.0:
raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
if not 0.0 <= final_lr:
raise ValueError("Invalid final learning rate: {}".format(final_lr))
if not 0.0 <= gamma < 1.0:
raise ValueError("Invalid gamma parameter: {}".format(gamma))
defaults = dict(lr=lr, betas=betas, final_lr=final_lr, gamma=gamma, eps=eps,
weight_decay=weight_decay, amsbound=amsbound)
super(AdaBoundW, self).__init__(params, defaults)
self.base_lrs = list(map(lambda group: group['lr'], self.param_groups))
def __setstate__(self, state):
super(AdaBoundW, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('amsbound', False)
def step(self, closure=None):
"""Performs a single optimization step.
Arguments:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
loss = None
if closure is not None:
loss = closure()
for group, base_lr in zip(self.param_groups, self.base_lrs):
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data
if grad.is_sparse:
raise RuntimeError(
'Adam does not support sparse gradients, please consider SparseAdam instead')
amsbound = group['amsbound']
state = self.state[p]
# State initialization 状态初始化
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p.data)
# Exponential moving average of squared gradient values
state['exp_avg_sq'] = torch.zeros_like(p.data)
if amsbound:
# Maintains max of all exp. moving avg. of sq. grad. values
state['max_exp_avg_sq'] = torch.zeros_like(p.data)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
if amsbound:
max_exp_avg_sq = state['max_exp_avg_sq']
beta1, beta2 = group['betas']
state['step'] += 1
# Decay the first and second moment running average coefficient
exp_avg.mul_(beta1).add_(1 - beta1, grad)
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)
if amsbound:
# Maintains the maximum of all 2nd moment running avg. till now
torch.max(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)
# Use the max. for normalizing running avg. of gradient
denom = max_exp_avg_sq.sqrt().add_(group['eps'])
else:
denom = exp_avg_sq.sqrt().add_(group['eps'])
bias_correction1 = 1 - beta1 ** state['step']
bias_correction2 = 1 - beta2 ** state['step']
step_size = group['lr'] * math.sqrt(bias_correction2) / bias_correction1
# Applies bounds on actual learning rate
# lr_scheduler cannot affect final_lr, this is a workaround to apply lr decay
final_lr = group['final_lr'] * group['lr'] / base_lr
lower_bound = final_lr * (1 - 1 / (group['gamma'] * state['step'] + 1))
upper_bound = final_lr * (1 + 1 / (group['gamma'] * state['step']))
step_size = torch.full_like(denom, step_size)
step_size.div_(denom).clamp_(lower_bound, upper_bound).mul_(exp_avg)
if group['weight_decay'] != 0:
decayed_weights = torch.mul(p.data, group['weight_decay'])
p.data.add_(-step_size)
p.data.sub_(decayed_weights)
else:
p.data.add_(-step_size)
return loss
SparseAdam
针对稀疏张量的一种“阉割版”Adam 优化方法。
A Method for Stochastic Optimization:
https://arxiv.org/abs/1412.6980
"""
optimizer.SparseAdam
torch.optimizer.SparseAdam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08)
稀疏版的Adam
主要参数:
params (iterable) – iterable of parameters to optimize or dicts defining parameter groups
lr (float, 可选) – 学习率(默认:1e-3)
betas (Tuple[float, float], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
"""
class SparseAdam(Optimizer):
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8):
sparse_params = []
for index, param in enumerate(params):
if isinstance(param, dict):
for d_index, d_param in enumerate(param.get("params", [])):
if d_param.is_sparse:
sparse_params.append([index, d_index])
elif param.is_sparse:
sparse_params.append(index)
if sparse_params:
raise ValueError(
f"Sparse params at indices {sparse_params}: SparseAdam requires dense parameter tensors"
)
defaults = dict(lr=lr, betas=betas, eps=eps)
super(SparseAdam, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if not grad.is_sparse:
raise RuntimeError('SparseAdam does not support dense gradients, please consider Adam instead')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
# Exponential moving average of squared gradient values
state['exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)
state['step'] += 1
grad = grad.coalesce() # the update is non-linear so indices must be unique
grad_indices = grad._indices()
grad_values = grad._values()
size = grad.size()
def make_sparse(values):
constructor = grad.new
if grad_indices.dim() == 0 or values.dim() == 0:
return constructor().resize_as_(grad)
return constructor(grad_indices, values, size)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
beta1, beta2 = group['betas']
# Decay the first and second moment running average coefficient
# old <- b * old + (1 - b) * new
# <==> old += (1 - b) * (new - old)
old_exp_avg_values = exp_avg.sparse_mask(grad)._values()
exp_avg_update_values = grad_values.sub(old_exp_avg_values).mul_(1 - beta1)
exp_avg.add_(make_sparse(exp_avg_update_values))
old_exp_avg_sq_values = exp_avg_sq.sparse_mask(grad)._values()
exp_avg_sq_update_values = grad_values.pow(2).sub_(old_exp_avg_sq_values).mul_(1 - beta2)
exp_avg_sq.add_(make_sparse(exp_avg_sq_update_values))
# Dense addition again is intended, avoiding another sparse_mask
numer = exp_avg_update_values.add_(old_exp_avg_values)
exp_avg_sq_update_values.add_(old_exp_avg_sq_values)
denom = exp_avg_sq_update_values.sqrt_().add_(group['eps'])
del exp_avg_update_values, exp_avg_sq_update_values
bias_correction1 = 1 - beta1 ** state['step']
bias_correction2 = 1 - beta2 ** state['step']
step_size = group['lr'] * math.sqrt(bias_correction2) / bias_correction1
p.add_(make_sparse(-step_size * numer.div_(denom)))
return loss
AdamW
_Adam: A Method for Stochastic Optimization:
https://arxiv.org/abs/1412.6980
… _Decoupled Weight Decay Regularization:
https://arxiv.org/abs/1711.05101
… _On the Convergence of Adam and Beyond:
https://openreview.net/forum?id=ryQu7f-RZ
class AdamW(Optimizer):
r"""Implements AdamW algorithm.
The original Adam algorithm was proposed in `Adam: A Method for Stochastic Optimization`_.
The AdamW variant was proposed in `Decoupled Weight Decay Regularization`_.
Arguments:
params (iterable): iterable of parameters to optimize or dicts defining
parameter groups
lr (float, optional): learning rate (default: 1e-3)
betas (Tuple[float, float], optional): coefficients used for computing
running averages of gradient and its square (default: (0.9, 0.999))
eps (float, optional): term added to the denominator to improve
numerical stability (default: 1e-8)
weight_decay (float, optional): weight decay coefficient (default: 1e-2)
amsgrad (boolean, optional): whether to use the AMSGrad variant of this
algorithm from the paper `On the Convergence of Adam and Beyond`_
(default: False)
..
"""
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8,weight_decay=1e-2, amsgrad=False):
defaults = dict(lr=lr, betas=betas, eps=eps,
weight_decay=weight_decay, amsgrad=amsgrad)
super(AdamW, self).__init__(params, defaults)
def __setstate__(self, state):
super(AdamW, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('amsgrad', False)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
# Perform stepweight decay
p.mul_(1 - group['lr'] * group['weight_decay'])
# Perform optimization step
grad = p.grad
if grad.is_sparse:
raise RuntimeError('AdamW does not support sparse gradients')
amsgrad = group['amsgrad']
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
# Exponential moving average of squared gradient values
state['exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)
if amsgrad:
# Maintains max of all exp. moving avg. of sq. grad. values
state['max_exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)
exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
if amsgrad:
max_exp_avg_sq = state['max_exp_avg_sq']
beta1, beta2 = group['betas']
state['step'] += 1
bias_correction1 = 1 - beta1 ** state['step']
bias_correction2 = 1 - beta2 ** state['step']
# Decay the first and second moment running average coefficient
exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
if amsgrad:
# Maintains the maximum of all 2nd moment running avg. till now
torch.maximum(max_exp_avg_sq, exp_avg_sq, out=max_exp_avg_sq)
# Use the max. for normalizing running avg. of gradient
denom = (max_exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(group['eps'])
else:
denom = (exp_avg_sq.sqrt() / math.sqrt(bias_correction2)).add_(group['eps'])
step_size = group['lr'] / bias_correction1
p.addcdiv_(exp_avg, denom, value=-step_size)
return loss
Rprop
该优化方法适用于 full-batch,不适用于 mini-batch,因而在 mini-batch 大行其道的时代里,很少见到。
"""
optimizer.Rprop
torch.optimizer.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
弹性反向传播
主要参数:
lr (float, 可选) – 学习率(默认:1e-2)
etas (Tuple[float, float], 可选) – 一对(etaminus,etaplis), 它们分别是乘法的增加和减小的因子(默认:0.5,1.2)
step_sizes (Tuple[float, float], 可选) – 允许的一对最小和最大的步长(默认:1e-6,50)
"""
class Rprop(Optimizer):
def __init__(self, params, lr=1e-2, etas=(0.5, 1.2), step_sizes=(1e-6, 50)):
defaults = dict(lr=lr, etas=etas, step_sizes=step_sizes)
super(Rprop, self).__init__(params, defaults)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if grad.is_sparse:
raise RuntimeError('Rprop does not support sparse gradients')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
state['prev'] = torch.zeros_like(p, memory_format=torch.preserve_format)
state['step_size'] = grad.new().resize_as_(grad).fill_(group['lr'])
etaminus, etaplus = group['etas']
step_size_min, step_size_max = group['step_sizes']
step_size = state['step_size']
state['step'] += 1
sign = grad.mul(state['prev']).sign()
sign[sign.gt(0)] = etaplus
sign[sign.lt(0)] = etaminus
sign[sign.eq(0)] = 1
# update stepsizes with step size updates
step_size.mul_(sign).clamp_(step_size_min, step_size_max)
# for dir<0, dfdx=0
# for dir>=0 dfdx=dfdx
grad = grad.clone(memory_format=torch.preserve_format)
grad[sign.eq(etaminus)] = 0
# update parameters
p.addcmul_(grad.sign(), step_size, value=-1)
state['prev'].copy_(grad)
return loss
RMSprop
实现 RMSprop 优化方法(Hinton ᨀ出),RMS 是均方根(root meam square)的意思。RMSprop 和 Adadelta 一样,也是对 Adagrad 的一种改进。RMSprop 采用均方根作为分母,可缓解 Adagrad 学习率下降较快的问题,并且引入均方根,可以减少摆动,详细了解可读:http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
https://arxiv.org/pdf/1308.0850v5.pdf
"""
optimizer.RMSprop
torch.optimizer.RMSprop(params,lr=0.01,alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
Adagrad的一种改进
主要参数:
lr (float, 可选) – 学习率(默认:1e-2)
momentum (float, 可选) – 动量因子(默认:0)
alpha (float, 可选) – 平滑常数(默认:0.99)
eps (float, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:1e-8)
centered (bool, 可选) – 如果为True,计算中心化的RMSProp,并且用它的方差预测值对梯度进行归一化
weight_decay (float, 可选) – 权重衰减(L2惩罚)(默认: 0)
"""
class RMSprop(Optimizer):
def __init__(self, params, lr=1e-2, alpha=0.99, eps=1e-8, weight_decay=0, momentum=0, centered=False):
defaults = dict(lr=lr, momentum=momentum, alpha=alpha, eps=eps, centered=centered, weight_decay=weight_decay)
super(RMSprop, self).__init__(params, defaults)
def __setstate__(self, state):
super(RMSprop, self).__setstate__(state)
for group in self.param_groups:
group.setdefault('momentum', 0)
group.setdefault('centered', False)
@torch.no_grad()
def step(self, closure=None):
loss = None
if closure is not None:
with torch.enable_grad():
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad
if grad.is_sparse:
raise RuntimeError('RMSprop does not support sparse gradients')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
#生成和括号内变量维度维度一致的全是零的内容
state['square_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
if group['momentum'] > 0:
state['momentum_buffer'] = torch.zeros_like(p, memory_format=torch.preserve_format)
if group['centered']:
state['grad_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
square_avg = state['square_avg']
alpha = group['alpha']
state['step'] += 1
if group['weight_decay'] != 0:
grad = grad.add(p, alpha=group['weight_decay'])
square_avg.mul_(alpha).addcmul_(grad, grad, value=1 - alpha)
if group['centered']:
grad_avg = state['grad_avg']
grad_avg.mul_(alpha).add_(grad, alpha=1 - alpha)
#执行元素级乘法。tensor1通过tensor2,将结果乘以标量。value然后把它加到input
avg = square_avg.addcmul(grad_avg, grad_avg, value=-1).sqrt_().add_(group['eps'])
else:
avg = square_avg.sqrt().add_(group['eps'])
if group['momentum'] > 0:
buf = state['momentum_buffer']
#用tensor2对tensor1逐元素相除,然后乘以标量值value 并加到tensor。
buf.mul_(group['momentum']).addcdiv_(grad, avg)
p.add_(buf, alpha=-group['lr'])
else:
p.addcdiv_(grad, avg, value=-group['lr'])
return loss