Logistic Regression 逻辑回归数学原理、python代码实现、实际应用

说在前面

第一次写博客，主要目的是再梳理一下学到东西的逻辑，如果可以帮助到其他在学习的人就更好啦。本篇主要参考的：《机器学习》西瓜书、博主文章：文章链接、以及知乎、百度等大神们的解惑文章
第一次写文章，会继续优化，有错误的地方请读者评论直接指出~~

线性回归模型的参数求解

线性模型（linear model），对应的是线性回归问题
线性模型公式：
【问题简化】先假设只有一个特征x 线性模型为：y=θx+b
我们的目的是：找到参数θ和b，使得线性模型的泛化性能最好，回归问题中我们用均方误差来度量模型的泛化性能

泛化性能：指模型在需要预测数据时的表现情况
怎么量化模型的泛化性能呢？用性能度量：
在回归任务种最常用的是 均方误差：均方误差是指 预测值和实际值差值的平方和 的均值

【问题转化为】求解θ和b，使得模型的均方误差最小

求均方误差最小时的参数值

令实际值为y（i），令根据模型的预测值为f（i），一共有m个i，E可以直接表示均值的意思
均方误差公式：

对于上面的均方误差公式来说，其实是关于参数θ和b的函数，也叫这个模型的损失函数，顾名思义：不同的θ和b 决定了模型在预测时的损失大小
求损失函数的极小值点，那分别对θ 和 b求一阶导数，并让一阶导数为0，得到的值就是损失函数的极小值点

一些名词解释：
最小二乘法：让均方误差最小的方法
最小二乘参数估计：让均方误差最小去求得参数θ和b的方法

一元线性函数拓展为多元线性函数

【问题拓展】更一般的线性模型是多元线性模型，即有很多个特征x，问题拓展为 求解多元线性回归模型
同一元线性模型一样，用的都是最小二乘参数估计法
单个x转化为X矩阵：

• 把参数b吸收到X矩阵里：归一化，让每个x除以b。归一化后的模型为Y=ΘX
• 同一元线性模型一样，写出模型的 均方误差，求均方误差最小的时候的参数值

多元线性模型的损失函数：
对损失函数求导后（公式里的x是矩阵x）：
让损失函数的一阶导数为0，求得Θ的值
在现实情况下，会有特征很多，甚至多于样例数的情况，这个时候会得到多个参数值，都可以让均方误差最小（这里涉及到矩阵的求解，暂时不展开解释）
这个时候选择哪个参数值，由学习算法的归纳偏好决定，常用的做法是 引入正则化项

【归纳偏好】：在选择模型的时候有一定的和任务相关的主观判断，成为归纳偏好
【正则化项】

• 正则化 可以理解为 规则化
• 目的是防止 过拟合
• 正则化项 有个正则化系数，系数越大，限制就越强，越使得误差函数更平滑

线性函数可以变形为复杂函数

【问题拓展】其实线性函数可以有很多种变形，所以一些复杂的模型函数都可以简化为线性函数模型做解答
可以有一个新的函数G，
，但是这个函数G 是需要可以被求导的（即需要是连续的函数），因为需要用最小二乘法求权重值（这个过程是需要求导的）

将回归模型拓展解决分类问题

在分类问题中，我们先看最简单的二分类问题
借用上一节得到的回归模型通用函数，借用回归模型解决二分类问题
那要找到合适的函数G
对于二分类来说， y 值只有两个选择 0 1 ，那么最理想的函数其实是 “单位跃阶”函数，但是单位跃阶函数不是连续函数（不能求导），所以要找一个代替的函数，最像的就是 对数几率函数了，也就是logistic function

单位跃阶函数：
x<0时，y=0
x=0时，y=0.5
x>0时 y=1

logistic Function 逻辑回归函数

是一种连续型的概率分布
分布函数公式：其中
,其中 ,μ是数学期望，也是分布的中心；γ表示散布程度，均方差
当μ=0，γ=1的时候，是标准的Logistict 分布，分布图如下，以（0，0.5）为轴对称点，当x>0时，y>0.5，当x<0时，y<0.5

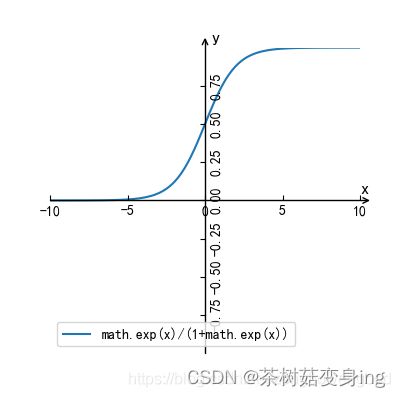
直接让 线性函数代替 t
在进行一番等式变换后（结合对数的转换）后公式变成
y可以认为是分类到正例的概率，1-y 就是分类到反例的发生概率，
反映了x作为正例的相对可能性，称为几率
几率取了对数，成为对数几率

【问题转化完成】所以目前分类的学习模型函数，从单位跃阶函数转化为了 对数几率线性回归模型 Logistic regression

Logistic Regression 模型的优点：

• 直接对分类可能性做建模，不需要假设数据分布，避免了假设分布不准带来的其他问题
• 不仅可以分出类别，还可以得到近似的概率
• 对数函数是任意阶可导的凸函数，又许多数值优化算法可直接用于求取最优解

Logistic Regression 对数几率线性回归模型（即逻辑回归模型）参数估计

怎么求得概率函数里的参数值呢？这时候可以用到极大似然法，让每个样本属于真是标记的概率越大越好

统计界有两个学派提供了不同的参数估计方法

• 频率主义学派
  认为参数是客观存在的固定值
  可以通过优化似然函数等准则来做参数估计
• 贝叶斯学派
  认为参数是随机变量，也有自己的分布
  需要假定参数服从一个先验分布，然后基于观察到的数据来计算参数的后验分布

极大似然法

我们这里用频率学派的参数估计方法： 极大似然法

极大似然估计（Maximum Likelihood Estimation MLE）：

• 极大似然估计是什么：
  是一种估计类条件概率的常用策略，现实假定具有某种确定的概率分布形式，然后再基于样本对概率分布的参数做估计。
• 什么样的模型可以用极大似然法？
  求解的模型需要是 有参数位置的概率分布模型
  有一些该模型生成的样本点
• 极大似然法的数据部分：似然函数
  把所有样本点都带入概率模型，然后再把它们相乘就得到了似然函数
  当似然函数最大的时候，就是这个参数最接近实际模型的时候
• 似然函数的变形：对数似然函数
  实际做计算的时候，很可能因为相乘的数据太多，导致下溢（计算机程序崩溃），做个简化：两边求对数后，就变成了所有特征带入模型后相加，似然函数被简化为：对数似然函数

对数似然函数公式：

P（yi）是把每个x值带入概率公式后求出来的结果概率
在二分类的问题中，结果只会有两个选项 0 或者1 ，因此P（yi）可以写成
yi*P（结果为1）+(1-yi)*P（结果为0）
解释：当yi=0 的时候 P（yi）=P（0） 当yi=1 的时候 P（yi）=P（1）
把P（yi）带入似然函数公式，就得到了逻辑回归模型的对数似然函数

【问题转换】求对数似然函数最大的时候，概率函数公式里的特征向量值为多少（就是未知的Θ和b）

梯度法求极大似然函数时的参数值

怎么求得呢？
可以用经典的数值优化算法：例如 梯度法（极大似然函数法里应该用梯度上升法）或者牛顿法

因为这里是求极大似然，因此需要用梯度上升法，
θ是权重值，α是步长，由于目标函数是θ的一次函数，求完一次导数后只剩下X矩阵了，error是用θ做预测模型得到的预测值和实际值y的差值

• 梯度上升法的公式： θ=θ+αX的转置error
• 梯度法说明：
  – 是一种常用的一阶优化方法（只使用目标函数的一阶导数，不利用高阶导数），利用目标函数的二阶导数，就是牛顿法，牛顿法计算复杂度高
  – 梯度法是用概率函数在某个点的导数来确认迭代方向
  – 每一次迭代都有一个步长，步子跨的太大容易错过极点，步子跨的过小需要学习的时间就太长
  梯度迭代的计算公式
  
  θ是迭代的点，长得像a的东西就是步长，后面的是对概率函数的一阶导数
  – 梯度上升法就是每次都加上迭代的步长，用来求概率函数的最大值，也就是求对数极大似然函数的最大值，梯度下降法是每次都减掉迭代的步长，是求误差最小化的算法

python代码实现逻辑回归模型

#!/usr/bin/python
# -*- coding:utf8 -*-
from numpy import *
import xlrd
#读取数据，并生成X和y的矩阵
def read_data():
    global datax
    global datay
    datax = []
    datay = []

    file = xlrd.open_workbook(r'C:\Users\little redred\Desktop\Download for work\repay_data.xlsx')
    sheet = file.sheet_by_index(0)

    for i in range(sheet.nrows):
        if i == 0:
            continue
        else:
            line = []
            for j in range(sheet.ncols):
                cell = sheet.cell(i, j).value
                line.append(cell)
            x=line[:8]
            x.append(1)
            #把θx+b 简化成一个  X 矩阵
            datax.append(x)
            datay.append(line[8])
    return datax , datay

# 定义sigmoid函数,也就是logistic 函数
def sigmoid(x):
    return 1 / (1 + exp(-x))

# 梯度上升法更新最优拟合函数
 @datax
 @datay
def gradAscent(m, n):
    # 把特征列表转换为Numpy矩阵
    dataxMetric = mat(datax)
    datayMetric = mat(datay).transpose()
    # 学习步长
    alpha = 0.001
    # 最大迭代次数
    maxCycles = 20000
    # 特征数据集的 行数和列数
    m, n = shape(dataxMetric)
    # 初始化每一个特征的权重都是1
    weights = ones((n, 1))

    # 循环迭代：
    for i in range(maxCycles):
        # 将特征矩阵和初始化的权重矩阵都计算一次，求sigmoid函数的值
        #这一步就是将线性方程转化为logistic 函数（也就是sigmoid函数）
        #dataxMetric * weights 就是 θ*X
        h = sigmoid(dataxMetric * weights)
        # 求预测值和实际值之间的差
        error = (datayMetric - h)
        # 更新权重系数，θ*x 对θ求一次导数，就是X 本身，X 是m*n
        weights = weights + alpha * dataxMetric.transpose() * error
    return weights

# 梯度上升算法在每次更新回归系数的时候需要遍历整个数据集，成本较高，优化一下，每次只用一个样本点来更新回归系数，成为  随机梯度上升法

def stocGradAscent(x, y):
    m, n = shape(x)
    alpha = 0.001
    weights = ones(n)
    x = array(x)
    for i in range(m):
        h = sigmoid(sum(x[i] * weights))
        error = y[i] - h
        weights = weights + alpha * error * x[i]
    print(type(x[i]))
    return weights

 但是每次只用一个点的数值 学习的话，可能得到的不是最优解
#因此再优化一下，随机选择

def new_stocGradAscent(x, y, number_iter=1000):
    m, n = shape(x)
    alpha = 0.01
    weights = ones(n)
    x = array(x)

    for j in range(number_iter):
        dataindex = list(range(m))
        for i in range(m):
            # 每次迭代调整下alpha，随着i j 的逐步增大，最开始alpha的步子还比较大，随着迭代的进行，alpha的步子越来越小
            alpha = 4 / (1 + i + j) + 0.01
            # 随机选取特征数据来更新参数
            # 随机生成一个 0 和 特征长度中间的一个数值
            randIndex = int(random.uniform(0, len(x)))
            # 用随机选中的数据点更新
            h = sigmoid(sum(x[randIndex] * weights))
            error = y[randIndex] - h
            weights = weights + alpha * error * x[randIndex]
            # 每次迭代都减掉用过的特征数据
            x = np.delete(x, randIndex, axis=0)
        return weights
        
# 用x 和 权重值 计算 sigmoid 值，如果大于0.5 返回1 其他返回0
def classifyVector(inX, weights):
    p = sigmoid(sum(inX * weights))
    if p > 0.5:
        return 1
    else:
        return 0

#得到训练出来的权重在测试集上的 泛化误差，这里用的是  错误率
def Test(x_test,y_test,trainWeights):
    num = 0
    error_count = 0

    for i in range(len(x_test)):
        num += 1
        if int(classifyVector(x_test[i], trainWeights)) != int(y_test[i]):
            error_count += 1
    erroRate = (float(error_count) / num)
    return erroRate

sklearn 包中的逻辑回归方法应用

from sklearn import metrics
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
#StandardScaler 用来做数据标准化：就是让数据都集中在0 附近，标准差为1，新得到的数据集方差为1，均值为0
from sklearn.preprocessing import StandardScaler
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import model_selection

datax,datay=read_data()
#把样本数据集X 标准化
standard_datax=StandardScaler().fit_transform(datax)
#数据分层采样,random_state 是随机数种子，种子不同每次的采样也不同，shuffle 洗牌模式，True 每次抽样都会打乱顺序
x_train, x_test, y_train, y_test = train_test_split(standard_datax, datay, test_size=0.4, random_state=20, shuffle=True)
#用Logistic Regression 模型训练数据
model=LogisticRegression().fit(x_train,y_train)
#model.coef_   就是模型里的theta值  model.intercept_ 就是b 的值
# print(model.coef_)
# print(model.intercept_)
#得到模型预测结果
y_pre=model.predict(x_test)
#求出模型的准确率,0.993
acc=accuracy_score(y_test,y_pre)
#再用全部的数据学习一个模型
model_al=LogisticRegression().fit(standard_datax,datay)

#用交叉验证法获取模型的预测分数
scores=model_selection.cross_val_score(model_al,standard_datax,datay,cv=5)
print(scores)
print(scores.mean())

【本篇只涉及一个模型，还未涉及到多个学习模型的对比，以下只是一些可以对比的 性能度量实现，可供参考】
#绘制PR曲线,这个函数的返回值依次为：查准率  查全率 ，用于计算查准率和查全率的阈值，可以包住另一个PR曲线的模型更好
# pr_line=sklearn.metrics.precision_recall_curve(y_test,y_pre)
# PR 曲线还是会有一些局限，例如如果两个模型的PR曲线相交了呢？哪个更好呢，其实更常用的是F1 度量， 计算F1 度量,0.498
#F1 度量是 查全率 和 查准率一样重要的情况，如果给它们加上不同的权重，就是Fβ
f1=metrics.f1_score(y_test,y_pre,average="macro")
fb=metrics.fbeta_score(y_test,y_pre,beta=0.8)