Chapter9:Simulink建模与仿真
基于胡寿松主编的《自动控制原理》(第七版)附录的MATLAB控制系统简单教程,可直接阅读教材附录,内容完全一样,没有大改动。
9.Simulink建模与仿真
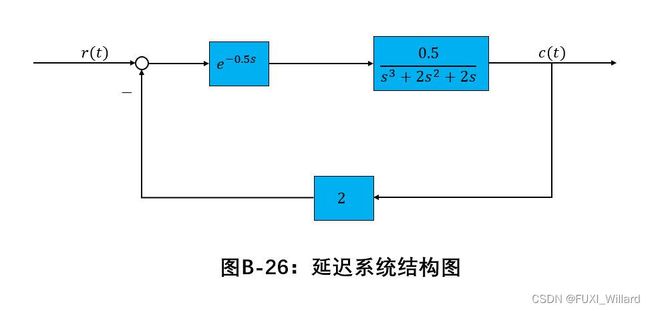
9.1 综合运用1:延迟系统的仿真
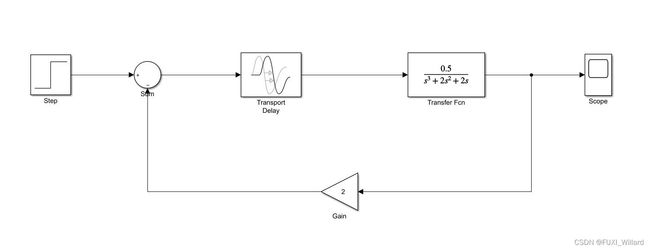
ExampleB-12: 设系统如下图所示,绘制该系统的单位阶跃响应曲线。
解:
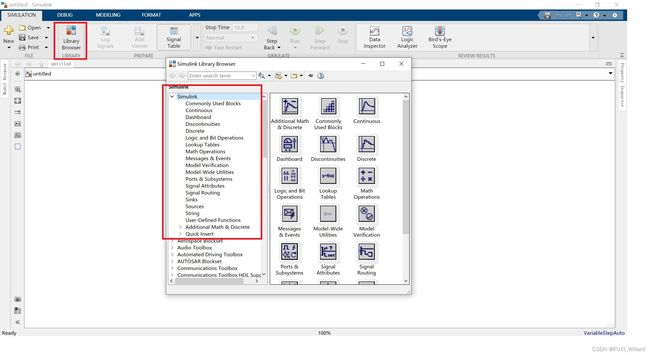
1.MATLAB交互命令行中输入:simulink打开仿真环境;
2.单击"Blank Model"新建模型;
3.打开"Library Browser"可见常见的仿真模块;
4.常见环节:
Continuous:连续环节;
Discontinuities:非线性环节;
Discrete:离散环节;
Math Operations:数学运算环节;
Sinks:输出方式;
Sources:输入源;
5.从对应模型库中拖曳相应的环节到界面;
具体步骤:
1.建立开环系统模型:
选择"Continuous(连续环节)"中的"Transfer Fcn(传递函数)"模块拖曳到模型窗口,双击模块即可修改参数;
2.添加延迟环节:
选择"Continuous(连续环节)"中的"Transport Delay(传递函数延迟环节)"模块拖曳到模型窗口,双击模块修改参数;
3.确立负反馈信号输入:
选择"Math Operations(数学运算环节)"中的"Sum(综合)"模块拖曳到模型窗口,把"List of sign"的编辑框的"++"修改为"+-"(负反馈);
4.添加增益环节:
选择"Math Operations(数学运算环节)"中的"Gain(增益)"模块拖曳到模型窗口,双击模块修改参数,并选择"Format|Flip Block"对模块进行翻转;
5.确定输入信号:
选择"Source(输入源)"中的"Step(阶跃输入信号)"模块拖曳到模型窗口,双击模块修改参数,将"Step time(阶跃时刻)"修改为0;
6.确定仿真输出方式:
选择"Sinks(输出方式)"中的"Scope(示波器)"模块拖曳到模型窗口;
7.模块连接;
8.完整模型如下图所示,双击示波器可显示结果;
9.2 综合运用2:复杂系统仿真
ExampleB-10:
设线性定常系统的状态方程为:
x ˙ ( t ) = [ − 2 − 2.5 − 0.5 1 0 0 0 1 0 ] x ( t ) + [ 1 0 0 ] u ( t ) , y ( t ) = [ 1 4 3.5 ] x ( t ) , x ( 0 ) = [ 1 − 0.75 0.4 ] \dot{x}(t)= \begin{bmatrix} -2 & -2.5 & -0.5\\ 1 & 0 & 0\\ 0 & 1 & 0 \end{bmatrix}x(t)+ \begin{bmatrix} 1\\0\\0 \end{bmatrix}u(t),y(t)= \begin{bmatrix} 1 & 4 & 3.5 \end{bmatrix}x(t),x(0)= \begin{bmatrix} 1\\-0.75\\0.4 \end{bmatrix} x˙(t)=⎣ ⎡−210−2.501−0.500⎦ ⎤x(t)+⎣ ⎡100⎦ ⎤u(t),y(t)=[143.5]x(t),x(0)=⎣ ⎡1−0.750.4⎦ ⎤
问:
- 能否通过状态反馈将系统的闭环极点配置在 − 1 、 − 2 、 − 3 -1、-2、-3 −1、−2、−3处?如有可能,求上述极点配置的反馈增益向量 k k k;
- 当系统的状态不可直接测量时,能否通过状态观测器来获取状态变量?如有可能,设计一个极点位于 − 3 、 − 5 、 − 7 -3、-5、-7 −3、−5、−7的全维状态观测器.
解:
【设计步骤】
-
检查系统的可控、可观测性。若被控系统可控可观测,则满足分离定理,用状态观测器估值形成状态反馈时,其系统的极点配置和观测器设计可分别独立进行;
-
对于系统 x ˙ = A x + b u \dot{x}=Ax+bu x˙=Ax+bu,选择状态反馈控制律 u = − k x + v u=-kx+v u=−kx+v,使得通过反馈构成的闭环系统极点,即 ( A − b k ) (A-bk) (A−bk)的特征根配置在期望极点处;
-
构造全维状态观测器 x ^ ˙ = A x ^ + b u − h c ( x ^ − x ) = ( A − h c ) x ^ + b u + h y \dot{\hat{x}}=A\hat{x}+bu-hc(\hat{x}-x)=(A-hc)\hat{x}+bu+hy x^˙=Ax^+bu−hc(x^−x)=(A−hc)x^+bu+hy,设计观测器输出反馈阵 h h h,使得观测器极点,即 ( A − h c ) (A-hc) (A−hc)的特征根位于期望极点处;
-
利用分离定理分别设计上述状态反馈控制律和观测器,得复合系统动态方程为:
[ x ˙ x ^ ˙ ] = [ A − b k h c A − b k − h c ] [ x x ^ ] + [ b b ] v , y = [ c 0 ] [ x x ^ ] \begin{bmatrix} \dot{x}\\ \dot{\hat{x}} \end{bmatrix}= \begin{bmatrix} A & -bk\\ hc & A-bk-hc \end{bmatrix} \begin{bmatrix} x\\ \hat{x} \end{bmatrix}+ \begin{bmatrix} b\\ b \end{bmatrix}v,y= \begin{bmatrix} c & 0 \end{bmatrix} \begin{bmatrix} x\\ \hat{x} \end{bmatrix} [x˙x^˙]=[Ahc−bkA−bk−hc][xx^]+[bb]v,y=[c0][xx^]
% exampleB_10.m
% 状态方程各矩阵
A=[-2 -2.5 -0.5;1 0 0;0 1 0];
b=[1 0 0]';
c=[1 4 3.5];
d=0;
N=size(A);n=N(1);
sys0=ss(A,b,c,d); % 系统状态空间模型;
S=ctrb(A,b) % 可控性矩阵;
f=rank(S);
if f==n
disp('system is controlled')
else
disp('system is not controlled')
end
V=obsv(A,c) % 可观测性矩阵;
m=rank(V);
if m==n
disp('system is observable')
else
disp('system is not observable')
end
P_s=[-1 -2 -3]; % 系统的期望配置极点;
k=acker(A,b,P_s) % 计算系统的反馈增益向量k;
P_o=[-3 -5 -7]; % 观测器的期望配置极点;
h=(acker(A',c',P_o))' % 计算观测器输出反馈向量;
A1=[A -b*k;h*c A-b*k-h*c];
b1=[b;b];
c1=[c zeros(1,3)];
d1=0;
x0=[1 -0.75 0.4]';
x10=[0 0 0]';
sys=ss(A1,b1,c1,d1); % 建立复合系统动态模型;
t=0:0.01:4;
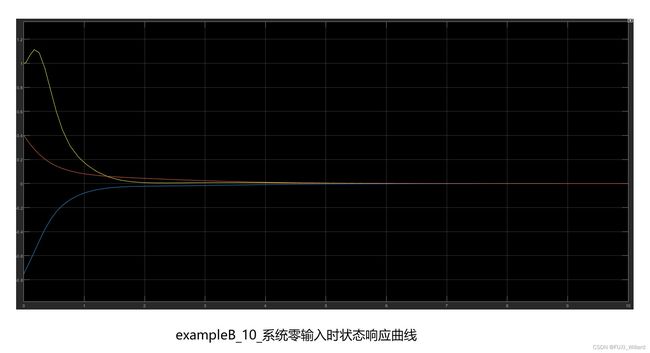
[y,t,x]=initial(sys,[x0;x10],t); % 计算系统的零输入响应;
figure(1)
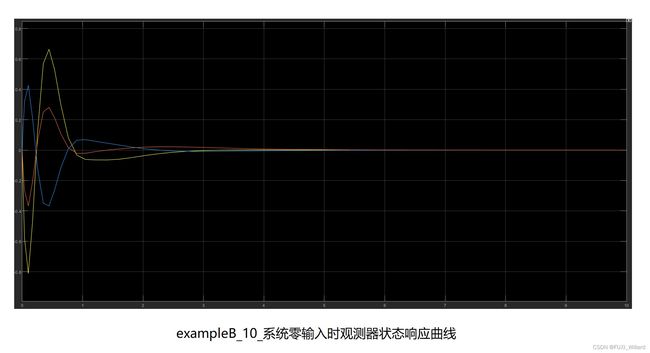
plot(t,x(:,1:3));grid; % 零输入响应系统状态曲线;
xlabel('t(s)');ylabel('x(t)');
figure(2)
plot(t,x(:,4:6));grid; % 零输入响应观测状态曲线;
xlabel('t(s)');ylabel('x(t)');
figure(3)
plot(t,(x(:,1:3)-x(:,4:6)));grid; % 零输入响应状态误差曲线;
xlabel('t(s)');ylabel('e(t)');
【结果分析】
-
结果如下:
S = 1.0000 -2.0000 1.5000 0 1.0000 -2.0000 0 0 1.0000 system is controlled V = 1.0000 4.0000 3.5000 2.0000 1.0000 -0.5000 -3.0000 -5.5000 -1.0000 system is observable可见系统完全可控可观测;
-
反馈增益向量和观测器输出反馈向量如下:
k = 4.0000 8.5000 5.5000 h = 35.2324 -19.8169 16.2958
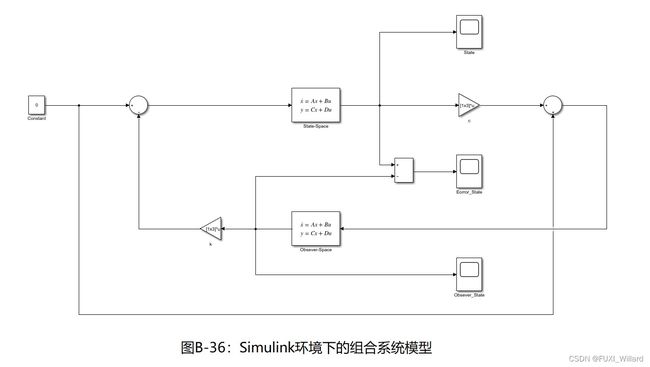
【使用Simulink仿真】
1.选择"Continuous(连续环节)"子模型库的"State-Space(状态空间)"模块,其参数为(上图中State-Space):
A=[-2 -2.5 -0.5;1 0 0;0 1 0],
b=[1;0;0],
c=eye(3),
d=[0;0;0],
Initial conditions=[1 -0.75 0.4]
2.选择"Math operations(数学运算)"子模型库的"Gain(增益)"模块,其参数为(上图中c):
[1 4 3.5],
Multiplication引导框选择"Matrix(K*u)";
3.选择"Continuous(连续环节)"子模型库的"State-Space(状态空间)"模块,其参数为(上图中Obsever-Space):
A=[-2 -2.5 -0.5;1 0 0;0 1 0]-[35.2324;-19.8169;16.2958]*[1 4 3.5],
b=[35.2324;-19.8169;16.2958],
c=eye(3),
d=[0;0;0]
4.选择"Math operations(数学运算)"子模型库的"Gain(增益)"模块,其参数为(上图中k):
[4 8.5 5.5],
Multiplication引导框选择"Matrix(K*u)";
5.选择"Sources(信号源)"子模型库的"Constant"模块,参数为:0
6.选择"Math operations(数学运算)"子模型库的"Sum"(两个)、"Add"(一个);
7.选择"Sink(输出)"子模型库的"Scope"模块(三个);
8.连线,run,然后双击"Scope"可得以下结果;
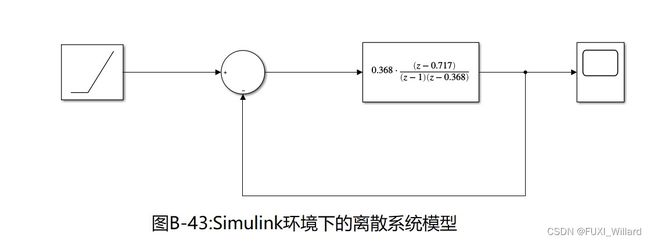
9.3 综合运用3:离散系统仿真
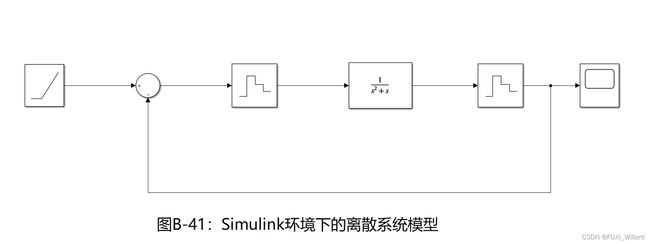
ExampleB-7: 设单位反馈线性定常离散系统的连续部分和零阶保持器的传递函数分别为:
G 0 ( s ) = 1 s ( s + 1 ) , G h ( s ) = 1 − e − s T s G_0(s)=\frac{1}{s(s+1)},G_h(s)=\frac{1-e^{-sT}}{s} G0(s)=s(s+1)1,Gh(s)=s1−e−sT
采样周期 T = 1 s T=1s T=1s;
解:
Simulink仿真模型如下:
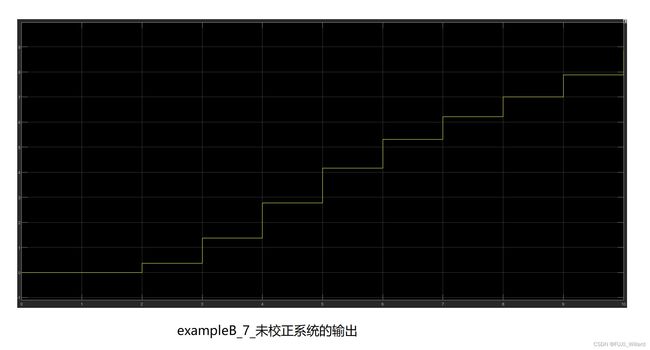
仿真结果如下:
Simulink模型亦可如下表示,仿真结果完全一样:
 自动控制原理理论基础参考链接
自动控制原理理论基础参考链接