YB菜菜的机器学习自学之路（一）——基础的罗森布拉特(Rosenblatt)感知器

@TOC

前提说明

想着以后雷达应用可能需要和深度学习什么的结果，在B站购买了《小白也能听懂的人工智能原理》想着听听学习学习，在这个假期，入个小小的门。 整点笔记方便自己以后回顾。

1.创建新工程

勉勉强强装了PyCharm和Anaconda，并尝试创建第一个新工程。
利用Anaconda Prompt创建一个虚拟环境， 大致步骤如下：

Step1：打开Anaconda Prompt，输入命令：

  conda create -n test python=3.7

创建了一个叫test的虚拟环境，python版本为3.7.

Step2: 接着输入命令：

activate test

进入自己的虚拟环境中。

step3：通过命令安装一些自己需要的库：

pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple

实现 比如matplotlib库的安装，其中后面的这个网址是清华源，为了稳定，更快的下载库用的。

Step4：这些弄好以后差不多就有了一个虚拟环境。可以通过命令查看conda环境里面是否有这个环境：

conda env list

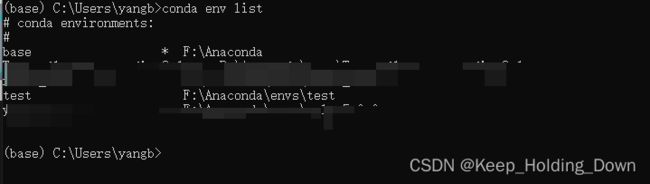
图1
如图1 ，可以看到 除了基础的conda自带的base环境，还有自己创造的test环境。

Step5：在PyCharm中建立一个新工程，并选择这个环境

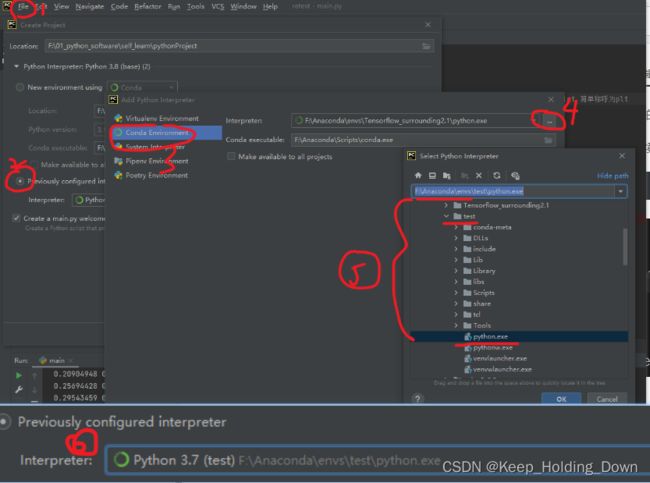图2
如图2，打开PyCharm，选择file–Newproject—previously configured interpreter—conda environment
打开目录，找到conda所在地方，找到conda-env–test里面的python.exe。
点确定就能看到图1（6）所示，再点确定，就能创建一个非常基础的工程。如图3所示。

图3

Step6：运行程序
我们可以在pycharm里面右键选择run “main”来运行主函数。
也可通过cmd运行。
命令如下：

图4
如图4所示，我的工程在F盘，所以首先打开CMD 然后激活环境，复制文件所在的目录。运行结束后要再输入对应的“盘：”，比如我是f盘，就需要输入“f:”。即，当前缀变成路径，而不再是系统C的时候，表示成功。
最后，输入py mian.py 再回车，就成功运行了函数。

2.罗森布拉特(Rosenblatt)感知器

图5 Rosenblatt感知模型和一元一次感知案例

图5展示了基础的Rosenblatt感知模型（图5蓝色部分）以及一个一元一次感知的实例（图五黑色部分）。
假设有一组观察值x,和y，要感知x和y之间的关系。
假设通过长期观察，我们估计他是一个线性关系，即y=wx，其中w为权重值。
为了获得w值，我们可以通过构建Rosenblatt感知模型让机器通过这组数据帮我们找到真实的w值。

step1：输入参数
首先我们将这些观察值的第一组数据（$x_1$,$y_1$）和权重值的初始值$w$输入进模型(这里w可以是任意大小的。

step2：构建期望函数得到预测值
因为通过观察，我们认为数据关系是一元一次函数，即 $y=wx$.
因此我们将观察数据带入到期望函数中，得到一个预测值：
$$Y_1=w\ast x_1(1)$$

step3: 通过与当前实际的观测值进行比较，获得误差：
$$e=y_1-Y_1(2)$$

step4: 获得新的权重值

在Rosenblatt中，新的权重值W的获得方式为：
$$W=w+e\ast x\ast \alpha （3）$$
其中，e表示由step3获得的当前预测值与实际值之间的误差，$\alpha$为学习率，它反映了w调整的快慢，如果$\alpha$太大，则可出现震荡，那么永远得不到真实的权重$w$。如果$\alpha$太小，则调整的太慢，效率太低，也有可能陷入局部解。

理论上$W=w+e\ast \alpha$就能满足条件，但是这种情况下，存在一个问题，如图6所示。

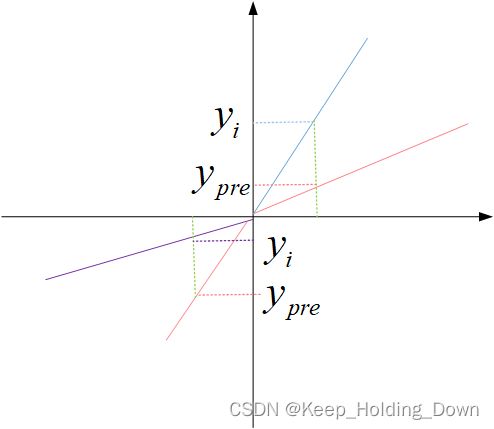
图6

假设权重值w的估计方式为$W=w+e\ast \alpha$。
在图6中，蓝色表示真正的斜率线，红色表示当前的斜率线。
假设输入的数据都是正值（$x_i>0,y_i>0$）, 此时预测值为$y_{pre}$。
那么误差$e=y_i-y_{pre}>0$.
按照客观情况，我们知道此时的w偏校，应增大w值:
按照公式$W=w+e\ast \alpha$可以得到 W>w，新的权重值W增大，符合规律。

但是如果数值是负的（$x_i<0,y_i<0$）,如图6中的第三象限：
其中紫色为真正的斜率，而红色表示当前的预测斜率。

理论上我们应该减少斜率，但是此时
误差$e=y_i-y_{pre}>0$.
按照公式$W=w+e\ast \alpha$，可以得到W>w，此时，调整出错。

为了解决这个方法，我们选择公式（3），即在误差项处再乘上输入参数x，由于x存在符号，就完美的解决了这个问题。
对于第三象限的情况，
按照公式$W=w+e\ast \alpha \ast x_i$,可以得到W

step5: 更新权重值w
即$w=W$

step6:进行下一次迭代
在下一次迭代中，$(x_2,y_2,新的w)$将作为输入参数进行新的一伦的迭代。

step7 ，当迭代满足条件或者此时，输出最终的权重w

最后，我们得到x与y的关系
$y=w_{last}\ast x$
即，机器通过感知模型实现了自主学习搜索。

结果展示

图7 1次迭代

图8 100次迭代

图9 一万次迭代