分数阶麻雀搜索算法-附代码
分数阶麻雀搜索算法
文章目录
- 分数阶麻雀搜索算法
-
- 1.麻雀优化算法
- 2. 改进麻雀算法
-
- 2.1 分数阶微积分
- 2.2 分数阶优化的麻雀搜索算法
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:采用分数阶微积分算法优化麻雀搜索算法,根据麻雀的位置信息,引入自适应分数阶阶次以自适应地调整分数阶阶次,加快算法收敛速度;
1.麻雀优化算法
基础麻雀算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/108830958
2. 改进麻雀算法
2.1 分数阶微积分
分数阶微积分与整数阶微积分对应, 是将微积分阶次从 整数推广到分数, 通过对整数微积分的差分近似递推求解极 限 [ 6 − 8 ] { }^{[6-8]} [6−8], 即阶次为分 数的微分和积分。最为常用的定义是 Grumwald-Letniko(G-L 定义)。
G-L 定义的离散表达式为 [ 9 ] { }^{[9]} [9] :
D v [ x ( t ) ] = 1 T v ∑ k = 0 β ( − 1 ) k γ ( v + 1 ) x ( t − k T ) γ ( k + 1 ) γ ( v − k + 1 ) (4) D^v[x(t)]=\frac{1}{T^v} \sum_{k=0}^\beta \frac{(-1)^k \gamma(v+1) x(t-k T)}{\gamma(k+1) \gamma(v-k+1)} \tag{4} Dv[x(t)]=Tv1k=0∑βγ(k+1)γ(v−k+1)(−1)kγ(v+1)x(t−kT)(4)
其中, v v v 为阶次; T T T 为周期; γ ( N ) = ∫ 0 ∞ e − t t n − 1 d t = ( n − 1 ) ! \gamma(N)=\int_0^{\infty} \mathrm{e}^{-t} t^{n-1} \mathrm{~d} t=(n-1) ! γ(N)=∫0∞e−ttn−1 dt=(n−1)! 为伽 马函数; β \beta β 为截止阶次。
2.2 分数阶优化的麻雀搜索算法
为了防止麻雀搜索算法陷入局部最优, 同时加快该算法 的收敛速度, 本文利用分数阶的学习训练算法易跳出局部极 值点的特点, 将麻雀搜索算法与分数阶微分相结合, 通过麻雀 群中麻雀位置的更新来自适应地调整分数阶次。
令式 (4) 中的 β = 4 \beta=4 β=4, 可得:
D v [ x ( t + 1 ) ] ≈ x ( t + 1 ) − v x ( t ) + 1 2 v ( v − 1 ) x ( t − 1 ) − 1 6 v ( v − 1 ) ( v − 2 ) x ( t − 2 ) + 1 24 v ( v − 1 ) ( v − 2 ) ( v − 3 ) x ( t − 3 ) (5) \begin{aligned} D^v[x(t+1)] \approx & x(t+1)-v x(t)+\frac{1}{2} v(v-1) x(t-1)-\\ & \frac{1}{6} v(v-1)(v-2) x(t-2)+\\ & \frac{1}{24} v(v-1)(v-2)(v-3) x(t-3) \end{aligned}\tag{5} Dv[x(t+1)]≈x(t+1)−vx(t)+21v(v−1)x(t−1)−61v(v−1)(v−2)x(t−2)+241v(v−1)(v−2)(v−3)x(t−3)(5)
由式 (5) 可知, 分数阶导数结果与当前项和之前的状态值 均有关, 且过去事件的影响随着时间的推移而减小。将分数 阶引入到麻雀搜索算法中发现者的位置更新处。由式 (1) 可 知, 当种群中的一些麻雀已经发现了捕食者, 并向种群中其他 麻雀发出警报时, 发现者的位置更新可描述为:
X i , j t + 1 − X i , j t = Q ⋅ L (6) X_{i, j}^{t+1}-X_{i, j}^t=Q \cdot \boldsymbol{L} \tag{6} Xi,jt+1−Xi,jt=Q⋅L(6)
式 (6) 的左边为分数阶 G − L \mathrm{G}-\mathrm{L} G−L 定义阶次 v v v 为 1 且周期 T T T 为 1 时的离散形式, 即:
D v [ x ( t + 1 ) ] = Q ⋅ L (7) D^v[x(t+1)]=\mathbf{Q} \cdot \boldsymbol{L} \tag{7} Dv[x(t+1)]=Q⋅L(7)
由式 (5) 可知, 当种群中的一些麻雀已经发现了捕食者, 并向种群中其他麻雀发出警报时, 发现者的位置更新可表 示为:
X i , j t + 1 = v X i , j t − 1 2 v ( v − 1 ) X i , j t − 1 − 1 6 v ( v − 1 ) ( v − 2 ) X i , j t − 2 + 1 24 v ( v − 1 ) ( v − 2 ) ( v − 3 ) X i , j t − 3 + Q ⋅ L (8) \begin{aligned} X_{i, j}^{t+1}=& v X_{i, j}^t-\frac{1}{2} v(v-1) X_{i, j}^{t-1}-\frac{1}{6} v(v-1)(v-2) X_{i, j}^{t-2}+\\ & \frac{1}{24} v(v-1)(v-2)(v-3) X_{i, j}^{t-3}+Q \cdot L \end{aligned} \tag{8} Xi,jt+1=vXi,jt−21v(v−1)Xi,jt−1−61v(v−1)(v−2)Xi,jt−2+241v(v−1)(v−2)(v−3)Xi,jt−3+Q⋅L(8)
可以看出, 分数阶次影响着发现者的位置更新。因此, 本 文采用自适应调整机制, 引入进化因子 f f f 对分数阶阶次 v v v 进 行修正。
(1) 当种群中的一些麻雀已经发现了捕食者, 并向种群中 其他麻雀发出警报时, 发现者 i i i 到其他麻雀的平均距离为:
d i x = 1 N − 1 ∑ j = 1 , j = i N ∑ k = 1 D ( x j k − x j k ) 2 (9) d_{i x}=\frac{1}{N-1} \sum_{j=1, j=i}^N \sqrt{\sum_{k=1}^D\left(x_{j k}-x_{j k}\right)^2} \tag{9} dix=N−11j=1,j=i∑Nk=1∑D(xjk−xjk)2(9)
其中, N N N 和 D D D 分别表示加入者的个数和维数。
(2) 在进化过程中, 进化因子 f f f 决定加入者当前的状态, 其定义为:
f = d g − d min d max − d min ∈ [ 0 , 1 ] (10) f=\frac{d_g-d_{\min }}{d_{\max }-d_{\min }} \in[0,1] \tag{10} f=dmax−dmindg−dmin∈[0,1](10)
其中, d g d_g dg 为全局最优位置到其他麻雀的平均距离; d max d_{\max } dmax 和 d min d_{\text {min }} dmin 分别为所有 d i x d_{i x} dix 中的最大值和最小值。
(3) 当分数阶阶次 v ∈ [ 0.5 , 0.8 ] v \in[0.5,0.8] v∈[0.5,0.8] 时, 收敛速度更快 [ 10 ] { }^{[10]} [10] 。 因此, v ( f ) = 1 2 e − 0.47 f ∈ [ 0.5 , 0.8 ] v(f)=\frac{1}{2} \mathrm{e}^{-0.47 f} \in[0.5,0.8] v(f)=21e−0.47f∈[0.5,0.8] 。
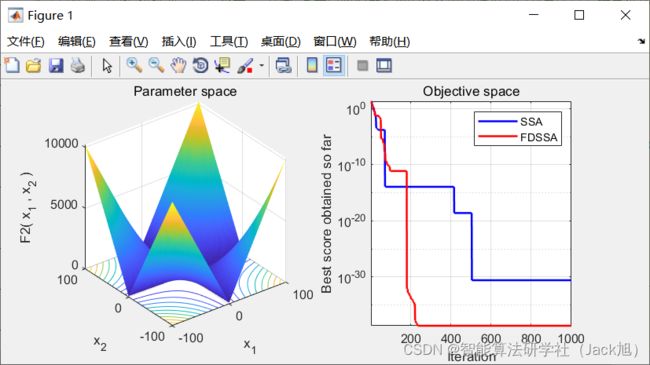
3.实验结果
4.参考文献
[1]江妍,马瑜,梁远哲,王原,李光昊,马鼎.基于分数阶麻雀搜索优化OTSU肺组织分割算法[J].计算机科学,2021,48(S1):28-32.