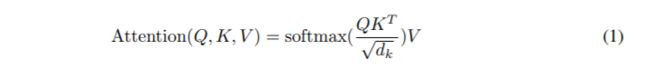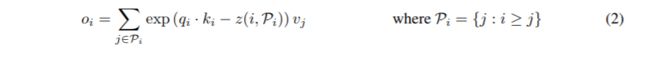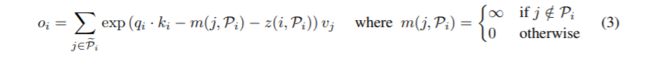解读Reformer

• 论文地址：https://openreview.net/forum?id=rkgNKkHtvB
• 代码：https://github.com/lucidrains/reformer-pytorch

介绍

Transformer 架构被广泛用于自然语言处理中，并且在许多任务中实现了 sota。为了获得这些结果，研究者不得不开始训练更大的 Transformer 模型。在最大的配置中，参数数量已经超过了 0.5B/层，层数多达 64。

诸如此类的大型 Transformer 模型频频出现，到底是客观上必须要求如此多的资源，还是仅仅是因为处理效率不够高？

如果说每层的内存占用只有这么一些的话，部署 Transformer 会比实际中更容易，但是事情并不是这样的。以上的估计只包括了每层的内存占用情况和输入的激活损失，并没有考虑 Transformer 上的内存占用问题：

• 由于激活需要被存储并用于反向传播，有着 N 层的模型的大小比单层大了 N 倍；
• 由于中间的全连接层的深度 d_ff 通常远大于注意力激活层的深度 d_model，因此需要占用很大的内存；
• 在长度为 L 的序列上的 attention 的计算和时间复杂度是 O(L2)，所以即使是一个有 64K 字符的序列就会耗尽 GPU 的内存。

研究者提出了一种 Reformer 模型来解决刚才说的那些问题：

• 可逆层（Reversible layer），在整个模型中启用单个副本，所以 N factor 就消失了；
• 在前馈层（feed-forward layer）分开激活和分块处理，消除 d_ff factor，节省前馈层的内存；
• 基于局部敏感哈希（locality-sensitive hashing，LSH）的近似注意力计算，让注意力层的 O(L2) 因子替代 O(L) 因子，实现在长序列上的操作。

局部敏感哈希注意力（LSH Attention）

Dot-product attention：

 

Multi-head attention：在多头注意力中，多个注意力层平行计算并叠加。每个注意力层会线性地投影 queries、keys 和 values head 次。

Memory-efficient attention：计算中可以发现，这种注意力机制带来的内存占用是很大的。回到公式 1，假设 Q、K、V 都有 [batch size, length, d_model] 这样的 shape。主要的问题就在于 QK^T，因为它的 shape 是 [batch size, length, length]。如果实验中序列的长度是 64k，在批大小为 1 的情况下，这就是一个 64K × 64K 的矩阵了，如果是 32 位浮点计算就需要 16GB 的内存。因此，序列越长，Transformer 性能就越受到影响。如果要减少内存占用的话，在这里就需要让 Q 和 K 保持一致。这是很容易的，只要从同样的线性层 A 提取即可，并单独分离一个给 V。QK 共享不会对 Transformer 的性能造成影响，即使对 K 加入额外的正则长度。

Hashing attention:对于局部敏感哈希注意力而言，需要 Q=K，以及 V，它们的 shape 都是 [batch size,length,d_model]，而重点关注的是 QK^T，有着 [batch size,length,length] 的 shape。进一步来说，对于每个 q_i，实际需要关注的是它们在 key 的接近值。例如，如果 K 是 64K，对于每个 q_i，只需要考虑一小部分，如 32 个到 64 个最接近的 keys。

Locality sensitive hashing:Reformer的论文选择了局部敏感哈希的angular变体。它们首先约束每个输入向量的L2范数(即将向量投影到一个单位球面上)，然后应用一系列的旋转，最后找到每个旋转向量所属的切片。这样一来就需要找到最近邻的值，这就需要局部敏感哈希（LSH）了，它能够快速在高维空间中找到最近邻。一个局部敏感哈希算法可以将每个向量 x 转换为 hash h(x)，和这个 x 靠近的哈希更有可能有着相同的哈希值，而距离远的则不会。在这里，研究者希望最近的向量最可能得到相同的哈希值，或者 hash-bucket 大小相似的更有可能相同。

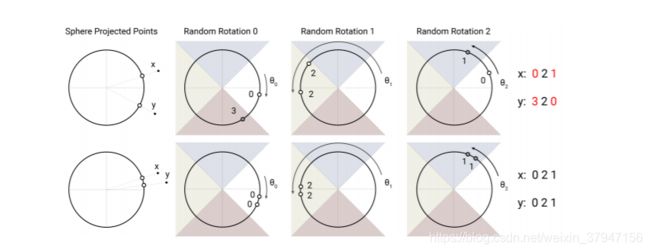
图1:局部敏感哈希算法使用球投影点的随机旋转，通过argmax在有符号的轴投影上建立bucket。在这个高度简化的2D描述中，对于三个不同的角哈希，两个点x和y不太可能共享相同的哈希桶(上图)，除非它们的球面投影彼此接近(下图)。

该图演示了一个用4个桶进行3轮哈希的设置。下面的图中的向量映射到了同一个bucket，因为它们的输入很接近，而上一张图中的向量映射到第一个和最后一个bucket。

找到给定的向量选择之后属于哪个桶也可以看成是找到和输入最一致的向量 —— 下面是Reformer的代码：

# simplified to only compute a singular hash
random_rotations = np.random.randn(hidden_dim, n_buckets // 2)
rotated_vectors = np.dot(x, random_rotations)
rotated_vectors = np.hstack([rotated_vectors, -rotated_vectors])
buckets = np.argmax(rotated_vectors, axis=-1)

把每个向量映射为一个哈希值叫做局部敏感哈希，如果比较近的向量能以高概率映射到同一个哈希值，而比较远的向量能以高概率被映射到不同的哈希值。为了得到个不同的哈希值，我们随机一个矩阵,大小为[dimension, b/2],然后定义h(x) = arg max([xR;−xR]) [u;v]表示两个向量的连接。这样，对所有的，我们就可以把它们分配到个哈希桶里面。

LSH attention:了解了我们的LSH方案和散列注意的一般思想之后，我们现在将正式定义我们在本文中使用的LSH注意。我们首先重写了正常注意的公式(1)，一次只查询一个位置i:

我们引入Pi表示在位置i处查询所处理的集合，z表示配分函数(即softmax中的规格化项)。为了清晰，我们还省略了的缩放。

出于成批处理的目的，我们通常对更大的集合Pei={0,1，…l}⊇Pi,掩盖元素不在Pi:

 

在为每个token计算一个桶之后，将根据它们的桶对这些token进行排序，并将标准的点积注意力应用到桶中的token的块上。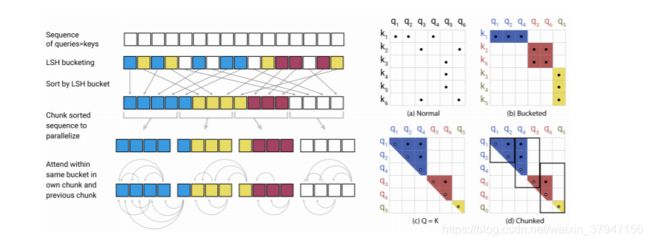

 图2:简化的局部敏感哈希注意力，展示了 hash-bucketing、排序和分块步骤，并最终实现注意力机制。

现在我们转向LSH注意力，我们可以把它看作是通过只允许一个散列桶中的注意力来限制我可以关注的查询位置的目标项的集合Pi。

图2(a-b)显示了全注意力与散列变体的示意图比较。第(a)部分描述了全注意的注意矩阵通常是稀疏的，但是计算没有利用这种稀疏性。在(b)中，查询和键按照它们的散列桶排序。由于相似的物品很有可能落在同一个桶里，所以只允许在每个桶里集中注意力就可以近似地得到完整的注意力模式。

在这种格式中，散列桶的大小往往不均匀，这使得很难跨桶进行批处理。此外，一个bucket中的查询数量和键的数量可能是不相等的——实际上，一个bucket可能包含许多查询，但是没有键。为了缓解这些问题，我们首先通过设置来确保h(kj) = h(qj)。接下来，我们根据桶号对查询进行排序，在每个桶内，根据序列位置对查询进行排序;这定义了一个排序后i 7→si的排列。在排序后的注意矩阵中，来自同一桶的对将聚集在对角线附近(如图2c所示)。我们可以采用成批处理的方法，其中m个连续的查询块(排序后)相互处理，一个块返回(图2d)。按照我们之前的符号，这对应于设置:

 

可逆 Transformer

虽然 LSH 解决了注意力的问题，但仍然存在一个内存的问题。一个网络的单层通常需要几 GB 的内存，并且通常适用于一个 GPU，所以即使是一个具有长序列的模型在只有一层的情况下也是可以执行的。但是，当训练一个具有梯度下降的多层模型时，需要保存每一层的激活值，以便在向后传递中使用。一个典型的 Transformer 模型有 12 个或更多的层，因此，如果用来缓存来自每个层的值，那么内存很快就会用完。

在 Reformer 中实现的第二个新方法是在反向传播期间按需重新计算每个层的输入，而不是将其存储在内存中。这是通过使用可逆层来实现的，其中来自网络的最后一层的激活被用来恢复来自任何中间层的激活，这相当于反向运行网络。在一个典型的残差网络中，栈中的每一层都不断地增加通过网络的向量。相反，可逆层对每个层有两组激活。一个遵循刚才描述的标准过程，并从一个层逐步更新到下一个层，但是另一个只捕获对第一个层的更改。因此，要反向运行网络，只需减去应用于每个层的激活。     

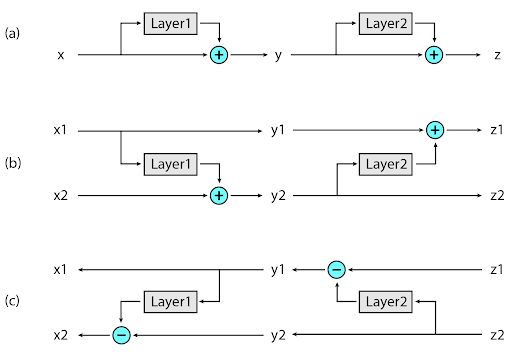
可逆层：(A)在标准残差网络中，每一层的激活用于更新到下一层的输入。(B)在可逆网络中，维持两组激活，每层后只更新其中一组。(C)这种方法使反向运行网络以恢复所有中间值成为可能。

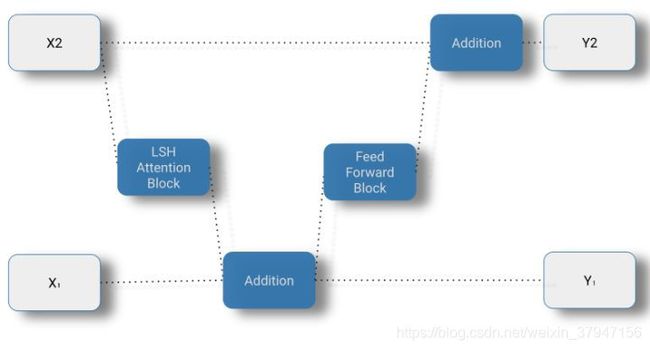
研究者在 Transformer 上应用了 RevNet 思想，将注意力和前馈层结合在 RevNet 块内。

常规的残差层执行一个作用于单个输入并产生单个输出的：

                                                                           

函数，其形式为 y = x + F (x)，可逆层作用于成对的输入/输出：

                                                            

并遵循以下方程：

在上面的公式中，F 成为注意力层，而 G 成为前馈层：

在实践中，Reformer定义f(x)是LSH注意力块，g (x)是标准的前向块，来自transformer结构。

分块

比较厚的层仍然会占用大量内存。前馈层的计算在序列中是完全独立的，所以可以分块：

一般这一层会通过执行所有位置的操作来进行批处理，但是每次进行一块的处理方法会减少内存占用，反向计算（reverse computation）和反向过程（backward pass）也会被分块。

code 如下：

# The full code is already open-source, but to retain anonymity we only submit
# the class below. It contains the most relevant parts for implementing LSH
# attention.
 
class MergedMultiHashedCausalAttentionV2(BaseCausalAttention):
  """Hash-based causal attention, with multiple hashes (faster version)."""
 
  def __init__(self, dropout, mode, n_bins=64, n_hashes=1, n_buckets=64,
               one_rng=False, allow_duplicate_attention=False,
               attend_across_buckets=False, hard_k=0,
               rehash_each_round=True, drop_for_hash_rate=0.0):
    del dropout
    self._mode = mode
    super(MergedMultiHashedCausalAttentionV2, self).__init__()
    assert n_buckets >= n_bins, 'This setting is not recommended: too few bins.'
    assert rehash_each_round or allow_duplicate_attention, (
        'The setting {allow_duplicate_attention=False, rehash_each_round=False}'
        ' is not implemented.')
    self.n_bins = n_bins
    self.n_hashes = n_hashes
    self.n_buckets = n_buckets
    self._drop_for_hash_rate = drop_for_hash_rate
    self._one_rng = one_rng
    self._prng = None
    if one_rng:
      seed = random.randint(0, 2**31 - 1)
      self._prng = backend.random.get_prng(seed)
 
    self._allow_duplicate_attention = allow_duplicate_attention
    self._attend_across_buckets = attend_across_buckets
    self._hard_k = hard_k
    self._rehash_each_round = rehash_each_round
 
  def call(self, inputs, params=(), state=(), rng=None, **kwargs):
    """Forward pass for the attention layer."""
    del params, kwargs
    output, _ = self.batch_call_and_or_grad(inputs[0], inputs[2], rng=rng)
    return output, state
 
  def call_and_grad(self, inputs, ct, rng=None, **kwargs):
    """Performs both forward and backward pass for the attention layer.
 
   This is used in reversible models: for the backward pass of a reversible
   model, we need to compute both the forward direction (to recover the
   previous layer's activations) and the backward direction simultaneously.
   Some computation can be shared between the forward and backward directions,
   which makes it more efficient to implement them jointly.
 
   This method assumes that the layer is stateless and has no parameters.
 
   Args:
     inputs: A tuple (q, k, v), where each element has shape
         n_batch*n_heads, seqlen, d_head
     ct: gradient signal for the layer output.
     **kwargs: kwargs for the layer
 
   Returns:
     A nested-tuple structure (output, (q_grad, k_grad, v_grad)) that contains
     the output of the forward pass and the gradient signal for each input.
   """
    del kwargs
    output, (qk_ct, v_ct) = self.batch_call_and_or_grad(
        inputs[0], inputs[2], ct=ct, rng=rng)
    return output, (qk_ct, np.zeros_like(inputs[1]), v_ct)
 
  def has_custom_grad(self):
    return True
 
  def custom_grad(self, inputs, output, ct, params=(), state=(), rng=None,
                  **kwargs):
    del output, params, state
    _, (qk_ct, v_ct) = self.batch_call_and_or_grad(
        inputs[0], inputs[2], return_output=False, ct=ct, rng=rng)
    inputs_ct = (qk_ct, np.zeros_like(inputs[1]), v_ct)
    return inputs_ct, ()
 
  def batch_call_and_or_grad(self, qk, v, ct=None, return_output=True,
                             rng=None):
    assert return_output or ct is not None, 'No work to perform!'
    # Hash bucket assignments are saved between the forward and reverse passes.
    # pylint: disable=protected-access
    stash_buckets = (return_output and ct is None
                     and base.Layer._STASH_IN is not None)
    if return_output and ct is not None and base.Layer._STASH_OUT is not None:
      buckets = base.Layer._STASH_OUT.pop(self)
    else:
      buckets = None
    # pylint: enable=protected-access
 
    # The approach here is to perform attention for one batch element and head
    # at a time. Note that there is absolutely no interaction across examples or
    # heads: this layer has no parameters, and hashing patterns are also
    # different across examples/heads. As a result, batching doesn't give any
    # performance gains except in the case of accelerator under-utilization. We
    # assume that hash-based attention will be applied primarily to long
    # sequences, where unbatched attention for a single head has sufficient
    # computation to fill up the accelerator.
 
    batch_loop_idx = np.zeros((), dtype=np.int32)
    batch_loop_max = qk.shape[0]
 
    init_vals = (batch_loop_idx,)
    if return_output:
      out_accum = np.zeros_like(qk)
      init_vals = init_vals + (out_accum,)
    if stash_buckets:
      buckets_accum = np.zeros(
          [qk.shape[0], self.n_hashes * qk.shape[1]], dtype=np.int32)
      init_vals = init_vals + (buckets_accum,)
    if ct is not None:
      qk_ct_accum = np.zeros_like(qk)
      v_ct_accum = np.zeros_like(v)
      init_vals = init_vals + (qk_ct_accum, v_ct_accum)
 
    def cond_fun(vals):
      batch_loop_idx = vals[0]
      return jax.lax.lt(batch_loop_idx, batch_loop_max)
 
    def body_fun(vals):
      """Performs attention for a single batch element and head."""
      batch_loop_idx = vals[0]
      if self._prng is None:
        hash_rng = jax.random.fold_in(rng, batch_loop_idx)
      else:
        # TODO: Maybe use the same RNG across examples (but not heads)?
        hash_rng = jax.random.fold_in(self._prng, batch_loop_idx)
      qk_slice = jax.lax.dynamic_index_in_dim(
          qk, batch_loop_idx, axis=0, keepdims=False)
      v_slice = jax.lax.dynamic_index_in_dim(
          v, batch_loop_idx, axis=0, keepdims=False)
 
      if buckets is None:
        buckets_slice = self.hash_vectors(qk_slice, rng=hash_rng)
      else:
        buckets_slice = jax.lax.dynamic_index_in_dim(
            buckets, batch_loop_idx, axis=0, keepdims=False)
 
      if ct is None:
        out_slice = self.single_call(
            qk_slice, v_slice, buckets_slice, hash_rng=hash_rng)
      else:
        def _do_single_call(qk_slice, v_slice):
          return self.single_call(
              qk_slice, v_slice, buckets_slice, hash_rng=hash_rng)
        ct_slice = jax.lax.dynamic_index_in_dim(
            ct, batch_loop_idx, axis=0, keepdims=False)
        out_slice, vjpfun = jax.vjp(_do_single_call, qk_slice, v_slice)
        qk_ct_slice, v_ct_slice = vjpfun(ct_slice)
 
      new_vals = (batch_loop_idx + 1,)
      if return_output:
        out_accum = vals[1]
        out_accum = jax.lax.dynamic_update_index_in_dim(
            out_accum, out_slice, batch_loop_idx, axis=0)
        new_vals = new_vals + (out_accum,)
      if stash_buckets:
        buckets_accum = vals[2]
        buckets_accum = jax.lax.dynamic_update_index_in_dim(
            buckets_accum, buckets_slice, batch_loop_idx, axis=0)
        new_vals = new_vals + (buckets_accum,)
      if ct is not None:
        qk_ct_accum, v_ct_accum = vals[-2:]
        qk_ct_accum = jax.lax.dynamic_update_index_in_dim(
            qk_ct_accum, qk_ct_slice, batch_loop_idx, axis=0)
        v_ct_accum = jax.lax.dynamic_update_index_in_dim(
            v_ct_accum, v_ct_slice, batch_loop_idx, axis=0)
        new_vals = new_vals + (qk_ct_accum, v_ct_accum)
 
      return new_vals
 
    final_vals = jax.lax.while_loop(cond_fun, body_fun, init_vals)
 
    if return_output:
      out = final_vals[1]
    else:
      out = None
 
    if stash_buckets:
      base.Layer._STASH_IN[self] = final_vals[2]  # pylint: disable=protected-access
 
    if ct is not None:
      input_ct = final_vals[-2:]
    else:
      input_ct = None
 
    return out, input_ct
 
  def make_unit_length(self, x, epsilon=1e-6):
    variance = np.mean(x**2, axis=-1, keepdims=True)
    norm_inputs = x / np.sqrt(variance + epsilon)
    return norm_inputs
 
  def drop_for_hash(self, x, rng):
    rate = self._drop_for_hash_rate
    if self._mode == 'train' and rate > 0.0:
      keep = backend.random.bernoulli(rng, 1.0 - rate, x.shape)
      return np.where(keep, x / (1.0 - rate), np.zeros_like(x))
    return x
 
  def hash_vectors(self, vecs, rng):
    # See https://arxiv.org/pdf/1509.02897.pdf
    # We sample a different random rotation for each round of hashing to
    # decrease the probability of hash misses.
    assert self.n_buckets % 2 == 0
    random_rotations_shape = (
        vecs.shape[-1],
        self.n_hashes if self._rehash_each_round else 1,
        self.n_buckets // 2)
 
    rng = jax.lax.tie_in(vecs, rng)
    rng, subrng = backend.random.split(rng)
    random_rotations = jax.random.normal(
        rng, random_rotations_shape).astype('float32')
    # TODO: the dropout mask will be used for all rounds of
    # hashing, so it's shared between them. Check if that's what we want.
    dropped_vecs = self.drop_for_hash(vecs, subrng)
    rotated_vecs = np.einsum('tf,fhb->htb', dropped_vecs, random_rotations)
    rotated_vecs = np.concatenate([rotated_vecs, -rotated_vecs], axis=-1)
 
    if self._rehash_each_round:
      buckets = np.argmax(rotated_vecs, axis=-1)
      # buckets is now (self.n_hashes, seqlen). Next we add offsets so that
      # bucket numbers from different hashing rounds don't overlap.
      offsets = jax.lax.tie_in(buckets, np.arange(self.n_hashes))
      offsets = np.reshape(offsets * self.n_buckets, (-1, 1))
      buckets = np.reshape(buckets + offsets, (-1,))
    else:
      # In this configuration, we map each item to the top self.n_hashes buckets
      rotated_vecs = np.squeeze(rotated_vecs, 0)
      bucket_range = jax.lax.tie_in(vecs, np.arange(rotated_vecs.shape[-1]))
      bucket_range = np.reshape(bucket_range, (1, -1))
      bucket_range = np.broadcast_to(bucket_range, rotated_vecs.shape)
 
      _, buckets = jax.lax.sort_key_val(
          rotated_vecs, bucket_range, dimension=-1)
      buckets = buckets[:, -self.n_hashes:]
      buckets = np.reshape(np.moveaxis(buckets, 0, -1), (-1,))
 
    return buckets
 
  def single_call(self, qk, v, buckets, hash_rng=None):
    # We use the same vector as both a query and a key.
    seqlen = qk.shape[-2]
    assert int(buckets.shape[0]) == self.n_hashes * seqlen
 
    ticker = jax.lax.tie_in(qk, np.arange(self.n_hashes * seqlen))
    buckets_and_t = seqlen * buckets + (ticker % seqlen)
    buckets_and_t = jax.lax.stop_gradient(buckets_and_t)
 
    # Hash-based sort ("s" at the start of variable names means "sorted")
    sbuckets_and_t, sticker = jax.lax.sort_key_val(
        buckets_and_t, ticker, dimension=-1)
    _, undo_sort = jax.lax.sort_key_val(sticker, ticker, dimension=-1)
    sbuckets_and_t = jax.lax.stop_gradient(sbuckets_and_t)
    sticker = jax.lax.stop_gradient(sticker)
    undo_sort = jax.lax.stop_gradient(undo_sort)
 
    st = (sticker % seqlen)
    sqk = np.take(qk, st, axis=0)
    sv = np.take(v, st, axis=0)
 
    # Split off a "bin" axis so that attention only occurs within chunks.
    bq_t = bkv_t = np.reshape(st, (self.n_hashes * self.n_bins, -1))
    bqk = np.reshape(sqk, (self.n_hashes * self.n_bins, -1, sqk.shape[-1]))
    bv = np.reshape(sv, (self.n_hashes * self.n_bins, -1, sv.shape[-1]))
    bq_buckets = bkv_buckets = np.reshape(
        sbuckets_and_t // seqlen, (self.n_hashes * self.n_bins, -1))
 
    # Hashing operates on unit-length vectors. Unnormalized query vectors are
    # fine because they effectively provide a learnable temperature for the
    # attention softmax, but normalizing keys is needed so that similarity for
    # the purposes of attention correctly corresponds to hash locality.
    bq = bqk
    bk = self.make_unit_length(bqk)
 
    # Allow each chunk to attend within itself, and also one chunk back. Chunk
    # boundaries might occur in the middle of a sequence of items from the
    # same bucket, so this increases the chances of attending to relevant items.
    def look_one_back(x):
      if len(x.shape) == 2:
        x_extra = np.concatenate([x[-1:, :], x[:-1, :]], axis=0)
      else:
        x_extra = np.concatenate([x[-1:, :, :], x[:-1, :, :]], axis=0)
      return np.concatenate([x, x_extra], axis=1)
 
    bk = look_one_back(bk)
    bv = look_one_back(bv)
    bkv_t = look_one_back(bkv_t)
    bkv_buckets = look_one_back(bkv_buckets)
 
    # Dot-product attention.
    dots = np.matmul(bq, np.swapaxes(bk, -1, -2)) / np.sqrt(bq.shape[-1])
 
    # Causal masking
    mask = jax.lax.convert_element_type(
        jax.lax.lt(bq_t[:, :, None], bkv_t[:, None, :]),
        np.float32)
    dots = dots - 1e9 * mask
 
    # Mask out attention to self except when no other targets are available.
    self_mask = jax.lax.convert_element_type(
        jax.lax.eq(bq_t[:, :, None], bkv_t[:, None, :]),
        np.float32)
    dots = dots - 1e6 * self_mask
 
    # Mask out attention to other hash buckets.
    if not self._attend_across_buckets:
      bucket_mask = jax.lax.convert_element_type(
          jax.lax.ne(bq_buckets[:, :, None], bkv_buckets[:, None, :]),
          np.float32)
      dots = dots - 1e5 * bucket_mask
 
    # Don't double-count query-key pairs across multiple rounds of hashing.
    # There are two possible strategies here. (1) The default is to count how
    # many times a query-key pair is repeated, and to lower its log-prob
    # correspondingly at each repetition. (2) When hard_k is set, the code
    # instead masks all but the first occurence of each query-key pair.
    # TODO: is one strategy faster or more numerically stable?
    if not self._allow_duplicate_attention:
      locs1 = undo_sort // bq_t.shape[-1]
      locs2 = (locs1 + 1) % (self.n_hashes * self.n_bins)
      if not self._attend_across_buckets:
        locs1 = buckets * (self.n_hashes * self.n_bins) + locs1
        locs2 = buckets * (self.n_hashes * self.n_bins) + locs2
      locs = np.moveaxis(np.concatenate([
          np.reshape(locs1, (self.n_hashes, seqlen)),
          np.reshape(locs2, (self.n_hashes, seqlen)),
      ], 0), 0, -1)  # produces shape (seqlen, 2 * self.n_hashes)
      slocs = np.take(locs, st, axis=0)
      b_locs = np.reshape(
          slocs, (self.n_hashes * self.n_bins, -1, 2 * self.n_hashes))
      # Queries always use the primary location (based on locs1).
      b_locs1 = b_locs[:, :, None, :self.n_hashes]
      if self._hard_k > 0:
        range_n_hashes = jax.lax.tie_in(b_locs, np.arange(self.n_hashes))
        nouse_locs = (range_n_hashes[:, None] > range_n_hashes[None, :])
        nouse_locs = 2 * nouse_locs - 1  # 1 = use, -1 = don't use
        nouse_locs = np.reshape(
            np.broadcast_to(nouse_locs[:, None, :],
                            (self.n_hashes, self.n_bins, self.n_hashes)),
            (self.n_hashes * self.n_bins, 1, 1, self.n_hashes))
        b_locs1 = b_locs1 * nouse_locs
      bq_locs = np.broadcast_to(
          b_locs1,
          b_locs.shape[:2] + (2, self.n_hashes))
      bq_locs = np.reshape(bq_locs, b_locs.shape)
      bkv_locs = look_one_back(b_locs)
 
      dup_counts = np.sum(
          jax.lax.convert_element_type(
              jax.lax.eq(bq_locs[:, :, None, :], bkv_locs[:, None, :, :]),
              np.float32),
          axis=-1)
      assert dup_counts.shape == dots.shape
      if self._hard_k > 0:
        dots = dots - 1e5 * jax.lax.stop_gradient(dup_counts)
      else:
        dots = dots - jax.lax.stop_gradient(np.log(dup_counts + 1e-9))
 
    # Each query only attends to the top k most relevant keys.
    if self._hard_k > 0:
      b_top_dots = np.sort(dots)[..., -self._hard_k:]  # Get the top k dots.
      b_top_dots = jax.lax.stop_gradient(b_top_dots)
      s_top_dots = np.reshape(b_top_dots, (-1, self._hard_k))
      top_dots = np.take(s_top_dots, undo_sort, axis=0)
 
      merged_top_dots = np.moveaxis(
          np.reshape(top_dots, (self.n_hashes, seqlen, self._hard_k)), 0, -1)
      merged_top_dots = np.reshape(merged_top_dots, (seqlen, -1))
 
      dots_thresh = np.sort(merged_top_dots)[:, -self._hard_k]
      # It's possible to compute the partition function at this point, but right
      # now this codepath isn't set up for backprop, and there might also be
      # issues computing it this way if two dot-products are exactly equal.
 
      sdots_thresh = dots_thresh[st]
      bdots_thresh = np.reshape(sdots_thresh, (self.n_hashes * self.n_bins, -1))
      bdots_thresh = jax.lax.stop_gradient(bdots_thresh)
 
      top_k_mask = jax.lax.convert_element_type(
          dots < bdots_thresh[..., None], np.float32)
      dots = dots - 1e5 * jax.lax.stop_gradient(top_k_mask)
 
    # Softmax.
    dots_logsumexp = backend.logsumexp(dots, axis=-1, keepdims=True)
    dots = np.exp(dots - dots_logsumexp)
 
    bo = np.matmul(dots, bv)
    so = np.reshape(bo, (-1, bo.shape[-1]))
    slogits = np.reshape(dots_logsumexp, (-1,))
 
    def unsort_for_output_impl(so, slogits):
      o = np.take(so, undo_sort, axis=0)
      # Sorting is considerably faster than gather, but first we need to work
      # around a compiler issue by introducing sticker_.
      sticker_ = sticker + jax.lax.convert_element_type(
          slogits[0] > 0, sticker.dtype)
      _, logits = jax.lax.sort_key_val(sticker_, slogits, dimension=-1)
      return o, logits
 
    def unsort_for_output_vjp(so, slogits):
      """Custom gradient for unsort_for_output."""
      so = jax.lax.stop_gradient(so)
      slogits = jax.lax.stop_gradient(slogits)
      o, logits = unsort_for_output_impl(so, slogits)
      def vjpfun(o_logits_grads):
        so_grad = np.take(o_logits_grads[0], sticker, axis=0)
        # TODO: this exists to match the forward pass, but I'm not sure
        # if it's actually required.
        buckets_and_t_ = buckets_and_t + jax.lax.convert_element_type(
            o_logits_grads[1][0] > 0, buckets_and_t.dtype)
        _, slogits_grad = jax.lax.sort_key_val(
            buckets_and_t_, o_logits_grads[1], dimension=-1)
        return (so_grad, slogits_grad)
      return (o, logits), vjpfun
 
    unsort_for_output = jax.custom_transforms(unsort_for_output_impl)
    jax.defvjp_all(unsort_for_output, unsort_for_output_vjp)
    o, logits = unsort_for_output_impl(so, slogits)
 
    if self.n_hashes == 1:
      out = o
    else:
      o = np.reshape(o, (self.n_hashes, seqlen, o.shape[-1]))
      logits = np.reshape(logits, (self.n_hashes, seqlen, 1))
      probs = np.exp(logits - backend.logsumexp(logits, axis=0, keepdims=True))
      out = np.sum(o * probs, axis=0)
 
    assert out.shape == v.shape
    return out

参考如下：

1、哈希革新Transformer：这篇ICLR高分论文让一块GPU处理64K长度序列

2、A Deep Dive into the Reformer