导数，偏导数，方向导数，梯度的理解---微积分数学基础

1. 导数的概念

那这里就产生了一个疑问：为什么使用梯度下降法求解？为什么使用梯度下降法，就能够得到最优解(全局或者局部)？
下边我们将从导数，偏导数，方向导数最后引出梯度，进而讲解为什么梯度下降法能够做到求解最优解。

1.1 导数的定义

增量定义： f(x)在点$x$₀ 的某个邻域内有定义，则当自变量 $x$ 在 $x$₀处取得增量Δx （点$x$₀ + Δx 仍然在邻域内），相应的y取得增量
Δy=f($x$₀+Δx)−f($x$₀)，如果Δ y与Δ x 在Δx → 0 时极限存在，则称 y=f(x)在$x$₀ 处可导，这个极限就是y=f(x)在$x$₀的导数，记为f′($x$₀)。

f′(x₀)=lim_Δx→0​ $\frac{\Delta x}{\Delta y}$ =lim_Δx→0 = $\frac{f(x0+\Delta x)-f(x0)}{\Delta x}$

极限定义：在定义域内，当变量x 趋近于x₀ 时，$\frac{f(x)-f\left(x_0\right)}{x-x_0}$有极限，则有f′(x₀) = $li{m}_{x\to x_0}\frac{f(x)-f\left(x_0\right)}{x-x_0}$

1.2 导数的本质

切线的斜率。物理角度上来看，路程对时间的导数叫速度，速度对时间的导数叫加速度。
   我们可以理解为这是一种线性近似，当一个函数为曲线时，我们对某一点的斜率，就是通过导数这种线性近似求得的。
   但是对于多元函数而言，由于其几何图形为一个曲面，这时候导数作为切线斜率的解释似乎不成立了，因此引入了偏导数的概念。

2. 偏导数的概念

2.1 偏导数定义

对于多元函数，求导数其实也是要求一个切线的斜率，但是由于曲面上的点的切线有无数条，那么取那条切线的斜率呢，这时候就引入了偏导数的概念。
   偏导数其实就是选取比较特殊的切线，求其斜率而得，以二元函数z=f(x,y)为例，分为对x 的偏导数和对y 的偏导数。
如图所示：

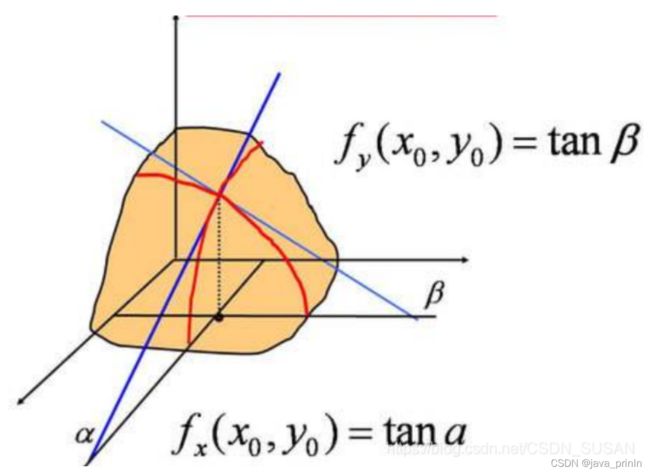
对x的偏导数： $\left(x_0,y_0,z_0\right)$垂直于y yy轴的曲线，在该点切线的斜率。
此时，该曲线可表示为
  z=f(x,y)
   x=t
   y=a+0×t
因此，我们求对x的偏导数，认为y是常量是完全正确的。
用导数定义来表示x的偏导数，
   $f_x\left(x_0,y_0\right)$=${\lim }_{\Delta x\to 0}\frac{f\left(x_0+\Delta x,y_0\right)-f\left(x_0,y_0\right)}{\Delta x}$f

对y 的偏导数：过点 $\left(x_0,y_0,z_0\right)$垂直于 x轴的曲线，在该点切线的斜率。
同上理解。
   f_y ( x₀ , y₀ ) = ${\lim }_{\Delta y\to 0}\frac{f\left(x_0,y_0+\Delta y\right)-f\left(x_0,y_0\right)}{\Delta y}$f

2.2 偏导数的本质

偏导数几何意义也是切线斜率， 但是由于曲面上一点的切线有无数条(实际上是个切面)，偏导数选取的是垂直于各坐标轴的几条特殊切线的斜率。
   偏导数物理意义表示函数沿着某个坐标轴方向上的变化率。
   但是如果我们想求任意一条曲线切线斜率怎么办呢?这时候就引入了方向导数，可以求出曲面上某一点沿着任意方向的切线斜率。

3. 方向导数

以z=f(x,y)为例，过曲面上任意一点$\left(x_0,y_0,z_0\right)$的所有切线，组成一个切面。偏导数仅仅选择了垂直于x和y轴方向的两条切线，计算斜率，方向导数则要求任意切向的斜率。
如下图所示

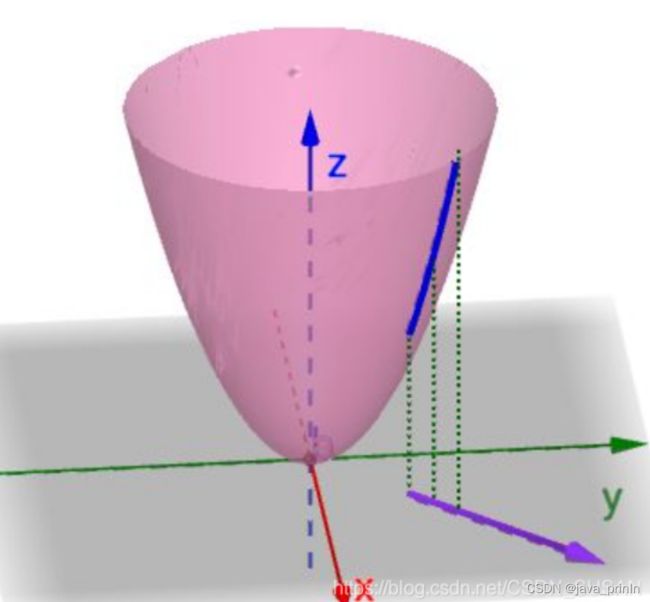
3.1 方向导数定义

x和y平面上的一个方向向量，决定了一条过点$\left(x_0,y_0,z_0\right)$的唯一曲线，此时曲线函数可表示为：
  z=f(x,y)
   $x=x_0+t\cos \alpha t\ge 0$
  $y=y_0+t\cos \beta t\ge 0$
  
  $u=i\cos \alpha +j\cos \beta =i\cos \alpha +j\sin \alpha$
 
   其中$\alpha$和$\beta$分别为该方向向量与x轴和y轴的夹角。
则该曲线的记为方向u的导数，定义：
   $D_{u}f(x,y)$ =${\lim }_{t\to 0}\frac{f\left(x_0+t\cos \alpha ,y_0+t\sin \alpha \right)-f\left(x_0,y_0\right)}{t}$
通过偏微分简化计算可得（这一步的数学证明，请自行搜索），
   $D_{u}f(x,y)$=$f_x(x,y)\cos \alpha +f_y(x,y)\sin \alpha$

3.2 方向导数的最大值

设偏导向量：
   $A=\left(f_x(x,y),f_y(x,y)\right)$

方向向量：
   $u=(\cos \alpha ,\sin \alpha )$ 则
   $D_{u}f(x,y)=A\ast u$ = $|A|\ast |u|\ast \cos (\theta )$

其中 θ 是偏导向量和方向向量之间的夹角。显而易见，当$\theta =0$时，$D_{u}f(x,y)$ 取得最大值。
   换句话说，当方向 $u$ 和偏导向量同向时，方向导数取得正最大值，反向时，取得负最大值。
   记住这个结论，接下来我们看梯度定义。

4. 梯度

4.1 梯度定义

对于函数z=f(x,y)，在平面区域D内具有一阶连续偏导数，则对于每一点 $\left(x_0,y_0\right)\in D$都可以定义出一个向量：
$f_x\left(x_0,y_0\right)i+f_y\left(x_0,y_0\right)j$
这个向量称为函数f(x,y)在 $\left(x_0,y_0\right)$ 的梯度，记作 $\mathrm{grad}f\left(x_0,y_0\right)$ 或者 $\nabla f\left(x_0,y_0\right)$ 。其中$\nabla =\frac{\partial }{\partial x}i+\frac{\partial }{\partial y}j$
​称为向量微分算子或者Nabla算子。

4.2 梯度生而最快

到这里，发现梯度就定义为偏导向量的方向。而方向导数一节已经证明，沿着偏导向量方向的方向导数$D_{u}f(x,y)$能够取得最大值。
因此在不断的迭代计算中，每一次沿着负梯度方向进行更新参数，就能够达到最低点。

5. 总结

通过导数，偏导数，方向导数的逐步讲解，最后给出梯度的定义，发现梯度天生定义就是变化最快的方向。
   这是未来使用梯度下降法求解优化问题的数学基础。

参考

https://www.zhihu.com/question/36301367 马同学和忆臻 的回答
https://github.com/halfrost/Halfrost-Field
https://blog.csdn.net/CSDN_SUSAN/article/details/90166474