线性回归和逻辑回归的梯度下降实现

1. 线性回归

（1）. 线性回归定义

线性回归：根据训练集所给数据建立一个线性方程，用于预测。属于有监督学习。
ps:回归在统计学中就表示一种预测性建模技术对自变量和因变量关系进行数学描述。

（2）. 代价函数

定义：指预测情况和真实情况的差距，用于衡量模型预测能力的好坏。

损失函数（Loss Function）：指单个样本的误差，用L表示。
代价函数（Cost Function）：指训练集的平均误差，用J表示。
但是在某些情况下写的这两个就是一个东西，都表示代价函数的意思。

线性回归的代价函数：

代价函数公式如下：
$$J（w,b）=\frac{1}{2m}\sum _{i=1}^m(\hat{y}{}^{(i)}-y^{(i)}{)}^2$$

使用的是最小二乘法，平方和最小相当于预测值和真实值距离最小。
那么当代价函数最小时，预测值最接近真实值。

（3）. 梯度下降

线性函数方程：f(x) = wx+b
回归就是要找出拟合度最高的w,b。
梯度下降方法是最常用的训练方法，通过找到令代价函数最小的参数，来确定最终的回归方程。

计算函数的梯度可以找到下降最快的方向，那么对于每一步都在梯度方向前进，最终会到达最小值。（但也可能是局部最小）
这种思想也是算法中的贪心思想。

现在问题就变成了：已知代价函数J（w,b）的式子，求让J最小的w,b。

大致思路是:先随机确定w,b的初始值（比如w=0,b=0）不断计算梯度，沿梯度下降方向更新，直至收敛在一个最小值周围。（收敛就是再更新值都不会有太大变化）

参数更新的公式就是：
$$w=w-\alpha \frac{\partial J(w,b)}{\partial w}$$
$$b=b-\alpha \frac{\partial J(w,b)}{\partial b}$$

（4）. python代码实现线性回归

import math,copy
import numpy as np
import matplotlib.pyplot as plt


def compute_cost(x,y,w,b):
	# 计算代价
    m = x.shape[0]
    cost = 0

    for i in range(m):
        f_wb = w * x[i] + b
        cost = cost + (f_wb - y[i])**2
    total_cost = 1 / (2*m)*cost

    return total_cost

def compute_gradient(x,y,w,b):
    m = x.shape[0]
    dj_dw = 0
    dj_db = 0
    #梯度都是直接根据公式求的
    for i in range(m):
        f_wb = w*x[i] + b
        dj_dw_i = (f_wb - y[i])* x[i]
        dj_db_i = f_wb - y[i]
        dj_db += dj_db_i
        dj_dw += dj_dw_i
    dj_dw = dj_dw / m
    dj_db = dj_db / m
    return dj_dw,dj_db

# 设置训练集，只是简单的两个数，真实情况会很多。
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])


def gradient_descent(x,y,w_in,b_in,alpha,num_iters, cost_function,gradient_function):
	#实现梯度下降
    w = copy.deepcopy(w_in)
    J_history = []  #开辟两个数组来存放历史记录，J_history代表代价函数
    p_history = []  #[w,b]的历史记录
    b = b_in
    w = w_in

    for i in range(num_iters):
        dj_dw, dj_db = gradient_function(x,y,w,b)
        b = b - alpha * dj_db
        w = w - alpha * dj_dw

        if i<100000:
            J_history.append(cost_function(x,y,w,b))
            p_history.append([w,b])
        # 每1000次打印一次
        if i%math.ceil(num_iters/10) == 0:
            #科学表达式
            print(f"Iteration{i:4}:Cost{J_history[-1]:0.2e}",
                  f"dj_dw:{dj_dw:0.3e},dj_db:{dj_db:0.3e}",
                  f"w:{w:0.3e},b:{b:0.5e}")

    return w,b,J_history,p_history

'''
有了以上函数直接训练就行
'''

# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iterations = 10000
tmp_alpha = 1.0e-2
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,
iterations, compute_cost, compute_gradient)

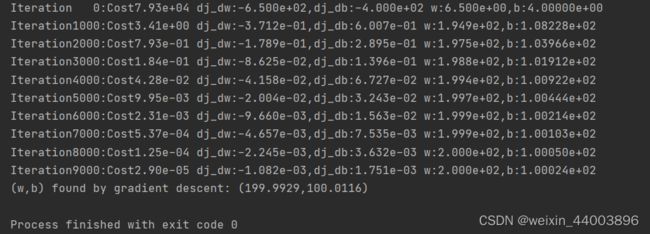
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")

运行结果如下图，可以看到随着迭代次数的增加，代价是不断减小的，最终会得到w=199.9929, b=100.0116：

2. 逻辑回归

对于分类问题，输出y只有两种可能，通常是yes,no问题。
这种问题适用于逻辑回归，虽然逻辑回归叫回归，但他解决的其实是分类问题。

（1）sigmoid函数

sigmoid 函数用于建立逻辑回归算法。
公式如下：
$$g(z)=\frac{1}{1+e^{-z}}$$
他总是把输出限定在0-1之间。

那么逻辑回归函数就表示成下面这个样子：
$$f(x)=\frac{1}{1+e^{-(wx+b)}}$$
f(x)他表示的意义是对于该问题的回答是yes的可能性大小。
x是所取得特征值。

（2）代价函数

首先逻辑回归是不能用线性回归的代价函数的。
因为使用了他就会变成非凸函数，有太多局部最小点，这样不能用梯度下降。
（图是在网上搜的）

对于逻辑回归使用的损失函数为交叉熵损失函数，也叫对数损失。
公式如下：
$$L(f(x^{(i)}),y^i)=\{\begin{array}{ll}& \text{-}log(f(x^{(i)}))，y^{(i)}=1\\ & \text{-}log(1-f(x^{(i)})),y^{(i)}=0\end{array}$$
用人话翻译过来就是：①当真实情况是1时，预测值越接近0，其损失越大。
②当真实情况是0时，预测值越接近1，损失越大。

那么综合这个式子就有：
$$L（f(x^{(i)}),y^{(i)}）=-y^{(i)}log(f(x^{(i)}))-(1-y^{(i)})log(1-f(x^{(i)}))$$
相当于把上面用数学方式写成了一个式子。
最后的代价函数就是取训练集数据的平均值
$$J(w,b)=\frac{1}{m}\sum _m^{i=1}[L(f(x^{(i)}),y^{(i)})]$$

3.梯度下降

思想和线性回归是一样的。
$$w=w-\alpha \frac{\partial J(w,b)}{\partial w}$$
$$b=b-\alpha \frac{\partial J(w,b)}{\partial b}$$
（求导部分自己算，发现线性回归和逻辑回归的求导结果是一样的，也就是它们的更新公式一模一样）

代码实现如下（两个特征值）：

import math,copy
import numpy as np
import matplotlib.pyplot as plt



'''
逻辑回归
'''
x_train = np.array([[0.5,1.5],[1,1],[1.5,0.5],[3,0.5],[2,2],[1,2.5]])
y_train = np.array([0,0,0,1,1,1])

def sigmoid(x):
    return 1/(1+math.exp(-x))

def compute_gradient_logistic(x,y,w,b):
    m,n = x.shape
    dj_dw = np.zeros((n,))
    dj_db = 0

    for i in range(m):
        f_wb_i = sigmoid(np.dot(x[i],w)+b)
        err_i = f_wb_i - y[i]
        for j in range(n):
            dj_dw[j] = dj_dw[j]+err_i*x[i,j]
        dj_db = dj_db + err_i
    dj_dw = dj_dw/m
    dj_db = dj_db/m
    return dj_db,dj_dw

def gradient_descent(x,y,w_in,b_in, alpha, num_iters):
    J_history = []
    w = copy.deepcopy(w_in)
    b = b_in

    for i in range(num_iters):
        dj_db,dj_dw = compute_gradient_logistic(x,y,w,b)

        w = w - alpha * dj_dw
        b = b - alpha * dj_db

        if i<100000 :
            J_history.append(compute_gradient_logistic(x,y,w,b))
        if i%math.ceil(num_iters/10)==0:
            print(f"Iteration{i:4d}:Cost{J_history[-1]}")
    return w,b,J_history

w_tmp = np.zeros_like(x_train[0])
b_tmp = 0.
alpha = 0.1
iters = 10000
w_out, b_out, _ = gradient_descent(x_train,y_train,w_tmp,b_tmp,alpha,iters)
print(f"\nupdated parameters:w:{w_out},b:{b_out}")

运行结果如下：

两个特征值为5.28和5.08，b为-14.22
最后得到的函数为：f(x)=1/(1+e^(5.28x1+5.08x2-14.22))