MATLAB实现频谱细化分析
一、函数调用
1.exzfft_ma函数
(1)函数格式:
[y,freq]=exzfft_ma(x,fe,fs,nfft,D)
其中x是被测信号,x的长度要大于ntff*D。fe是细化区间的中心频率,fs是采样频率,nfft是细化fft的长度,D是细化倍数。输出变量y是细化fft后的输出,freq是细化fft后的频率刻度。
(2)函数代码:
function [y,freq,c]=exzfft_ma(x,fe,fs,nfft,D)
nt=length(x); % 计算读入数据长度
fi=fe-fs/D/2; % 计算细化截止频率下限
fa=fi+fs/D; % 计算细化截止频率上限
na=round(0.5 * nt/D+1); % 确定低通滤波器截止频率对应的谱线条数
% 频移
n=0: nt-1; % 序列索引号
b=n*pi* (fi+fa)/fs; % 设置单位旋转因子
y=x.*exp(-1i*b); % 进行频移
b= fft(y, nt); % FFT
% 低通滤波和下采样
a(1: na) =b(1: na); % 取正频率部分的低频成分
a(nt-na+2 : nt) =b(nt-na+2 : nt); % 取负频率部分的低频成分
b=ifft(a, nt); % IFFT
c=b(1 : D: nt); % 下采样
% 求细化频谱
y=fft(c, nfft) * 2/nfft;% 再一次FFT
y=fftshift(y); % 重新排列
freq=fi+(0:nfft-1)*fs/D/nfft; % 频率设置
2.zoomffta函数
(1)函数格式:
[xz,f]=zoomffta(x,fs,N,fe,D,a);
N是fft长度,a决定了滤波器半阶数,D是细化倍数,fs是采样频率,fe是细化频带的中心频率
(2)函数代码:
function [xz,fz]=zoomffta(x,fs,N,fe,D,a)
M=round(4*D/a); % 滤波器半阶数
k=1:M;
w=0.5+0.5*cos(pi*k/M); % Hanning窗(半窗)
% 求取理想带通滤波器上下界;
fl=max(fe-fs/(4*D),-fs/2);
fh=min(fe+fs/(4*D),fs/2);
% 求取扩展带通滤波器上下界;
hfl=fl-(fh-fl)*a/2;
hfh=fh+(fh-fl)*a/2;
%构造扩展带通滤波器;
wl=2*pi*hfl/fs; % hfl和hfh归一化角频率
wh=2*pi*hfh/fs;
hr(1)=(wh-wl)/pi; % 按式(5-2-18a)计算复解析带通滤波器实部
hr(2:M+1)=(sin(wh*k)-sin(wl*k))./(pi*k).*w;
hi(1)=0; % 按式(5-2-18a)计算复解析带通滤波器虚部
hi(2:M+1)=(cos(wl*k)-cos(wh*k))./(pi*k).*w;
%重采样和滤波
for k=1:N
kk=(k-1)*D+M;
xrz(k)=x(kk+1)*hr(1)+sum(hr(2:M+1).*(x(kk+2:kk+M+1)+x(kk:-1:kk-M+1)));
xiz(k)=x(kk+1)*hi(1)+sum(hi(2:M+1).*(-x(kk+2:kk+M+1)+x(kk:-1:kk-M+1)));
end
%移频,把fl移到0频
yf=D*fl/fs; % 移频量
xz=(xrz+1j*xiz).*exp(-1j*2*pi*(0:N-1)*yf); % 移频
xz=fft(xz); % FFT
xz=xz(1:N/2)/N; % 取细化复数谱
fz=(0:N/2-1)*fs/N/D+fl; % 计算细化谱对应的频率
二、范例
1.调用exzfft_ma函数:
(1)代码:
clear all; clc; close all;
N=640; % 数据长度
fs=200; % 采样频率
t=(0:N-1)/fs; % 时间刻度
% 构成信号序列
x=10*sin(2*pi*32*t)+10*sin(2*pi*50*t)+20*sin(2*pi*54*t)+20*sin(2*pi*56*t)+30*sin(2*pi*59*t)+20*sin(2*pi*83*t);
nfft=64; % FFT长度
X=fft(x,nfft); % FFT分析
ff=(0:(nfft/2-1))*fs/nfft; % 频率刻度
n2=1:nfft/2; % 正频率索引号
X_abs=abs(X(n2))*2/nfft; % 正频率部分的幅值谱
fe=50; % 中心频率
D=10; % 细化倍数f
[y,freq]=exzfft_ma(x,fe,fs,nfft,D); % 细化分析
% 作图
figure(1)
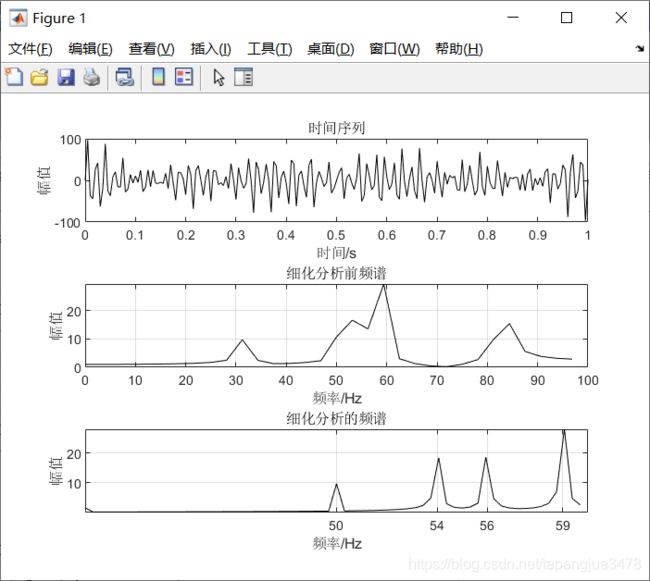
subplot 311; plot(t,x,'k');
xlabel('时间/s'); ylabel('幅值');
xlim([0 1]); title('时间序列');
subplot 312; plot(ff,X_abs,'k');
xlabel('频率/Hz'); ylabel('幅值');
title('细化分析前频谱'); grid;
subplot 313; plot(freq,abs(y),'k'); grid;
set(gca, 'XTickMode', 'manual', 'XTick', [50,54,56,59]);
set(gca, 'YTickMode', 'manual', 'YTick', [10,20,30]);
xlabel('频率/Hz'); ylabel('幅值');
title('细化分析的频谱');
set(gcf,'color','w');
(2)实验结果
2.调用zoomffta函数:
(1)代码:
clear all; clc; close all;
fs=2048; % 采样频率
nfft=1024; % FFT变换长度
fk=[50 150 496 498 500 502 505]; % 频率矩阵
A=[220 35 1 1 1 1 1]; % 幅值矩阵
D=100; % 细化倍数
a=0.3; % 外扩系数
L=nfft*D+round(8*D/a); % 数据长度
t=(0:L-1)/fs; % 时间刻度
x=zeros(1,L); % 初始化
for k=1 : 7 % 构成信号
x=x+A(k)*cos(2*pi*fk(k)*t);
end
fe=500; % 细化区间中心频率
[xz,f]=zoomffta(x,fs,nfft,fe,D,a); % 复解析滤波器复调制细化分析
% 作图
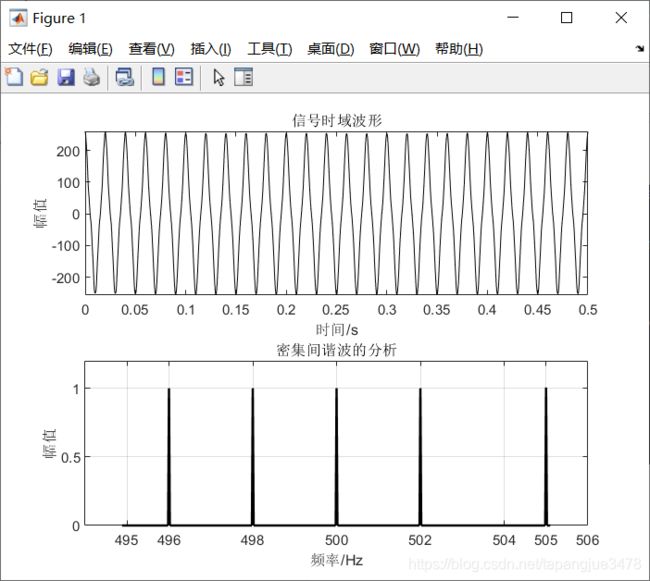
subplot 211; plot(t,x,'k'); xlim([0 0.5]);
xlabel('时间/s'); ylabel('幅值')
title('信号时域波形');
subplot 212; plot(f,abs(xz),'k','linewidth',1.5);
set(gca, 'XTickMode', 'manual', 'XTick', [495,496,498,500,502,504,505,506]);
grid; ylim([0 1.2]);
xlabel('频率/Hz'); ylabel('幅值')
title('密集间谐波的分析');
set(gcf,'color','w');