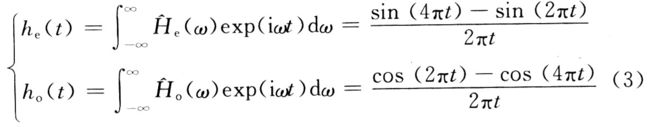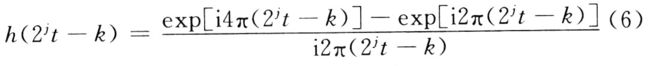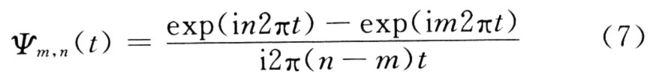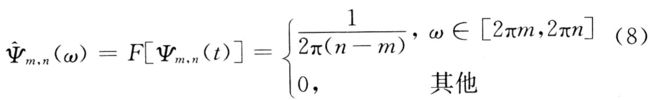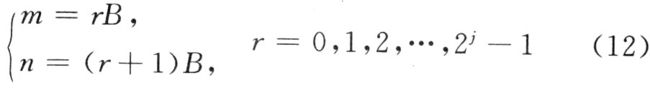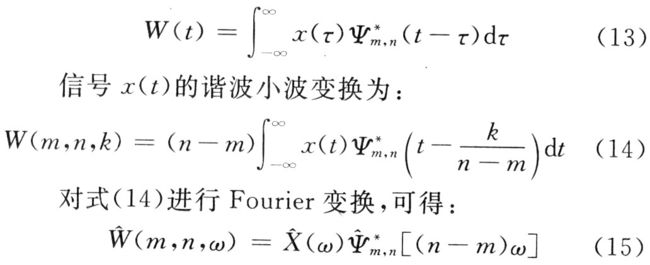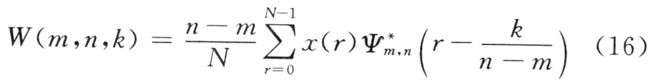谐波小波 matlab,基于谐波小波的电力系统谐波分析

摘要：电力系统中的谐波对电网危害巨大，对其进行监测和分析就显得非常重要。在谐波小波以及谐波小波包的基础上，提出谐波小波变换的表达式以及谐波小波算法，给出电力系统谐波分析的仿真示例。仿真结果表明，利用谐波小波变换分解，并通过最小二乘法拟合出的各次谐波频率和幅度的误差率完全符合谐波分析的精度要求。在电力系统谐波的分析中，谐波小波算法具有其他算法无可比拟的优越性。

关键词：谐波小波；谐波分析；电力系统；谐波；间谐波；最小二乘法拟合

0 引 言

由于电力系统中大量非线性设备的存在，导致它们在工作时不仅会产生基波频率的整数次谐波，还可能产生基波频率的非整次谐波，即间谐波，这会对电能造成严重的污染，增加能量损失，威胁电力设备的安全运行。因此，谐波和间谐波的分析对于电力系统的监控与保护都具有十分重要的意义。

传统的正交小波包变换在电力系统谐波分析与检测中有着广泛的应用。但是由于小波包变换固有的性质，如小波包变换的混叠现象比小波变换的混叠现象更为直观形象，其影响也比小波变换严重，这主要是由于分解滤波器之间存在频带混叠现象，小波频谱的起始频率和截止频率之间存在过渡带。谐波小波变换是一种基于快速傅里叶变换(Fast Fourier Transform，FFT)及其逆变换(Inverse Fast Fourier Transform，IFFT)的快速算法，在数值上容易实现，其算法快，精度高，具有很好的工程实用价值。通常的小波算法(如Mallat算法，Daubechies小波)在分解信号时要隔二取一，从而使得在小波分解时各层的数据点数和采样频率随尺度的增加逐渐减小。谐波小波相对于传统的小波函数而言，具有更普遍意义上的正交性以及优异的视频分解能力，其明显优势就是信号任意频段的“细化”能力，虽然它在时域中的局部化能力一般，但在频域分析中对精度有特殊要求的场合，这种优势就非常符合需求。

1 谐波小波分析

1.1 经典谐波小波

设时域函数h(t)和h(t)的傅里叶变换所对应的频域函数为Ｈｅ(ω)和Ｈ。(ω)，它们的表达式见式(1)：

式中：下标e和o分别表示该函数是变量ω的偶函数和奇函数。

将频域函数Ｈｅ(ω)和Ｈ。(ω)组成复合函数Ｈ(ω)，可得：

H(ω)具有良好的紧支撑特性和盒形特征。对式(1)作广义的傅里叶逆变换(忽略系数1/(2π))，可得：

将时域函数he(t)和h。(t)组成复合函数h(t)，可得：

由此定义的复合函数h(t)称为谐波小波函数，亦称为经典谐波小波或二进谐波小波，其实部he(t)和虚部h。(t)的波形如图1所示。

由图1可以看出，谐波小波h(t)是由相差90°的实部偶小波和虚部奇小波构成。虚部奇小波所构成的滤波器都是零相移滤波器，具有锁定信号相位的功能。它

在时域上的衰减速度较慢(与时间t成反比)，导致其时域局部化特性较弱。

为了获得谐波小波h(t)的二进伸缩平移系，令：

式中：j为非负整数；k为整数。

把式(5)代入式(4)，可得：

在式(6)中，小波的形状没有改变，只是在水平尺度上被压缩了2j，并且位置在新的尺度上被平移了k个单位，这与二进小波变换的形式是一致的。其j值决定谐波小波的尺度或层数。例如当j＝O时，谐波小波的傅里叶变换位于[2j+1π，4π]频带中；若在第j层时，则谐波小波的傅里叶变换位于[2j+1π，2j+2π]频带之间。即随着j值的增大，其频谱的带宽以二进方式逐渐加大。谐波小波对信号的分解从低频到高频是以2倍的关系逐渐增加的，它对信号的低频部分划分比较细，而对信号的高频部分划分比较粗，这说明经典谐波小波分解也属于二进小波分解的范畴。

1.2 谐波小波的改进

为了使分析频带的选取更为灵活，不受二进方式的限制，对经典谐波小波加以改进，拓宽谐波小波的概念及应用范围。引入正整数m一2j，n＝2j+1(m

其频域表达式为：

由式(7)可以看出，实际上m，n既可以取正整数，也可以取负整数，这样它们之间就不必满足，n＝2m这一条件的限制(二进限制)，只要保证m

若给定谐波小波的位移步长为k/(n－m)，k为整数，对式(7)进行平移变换可得：

由此可见，式(10)是分析频率带宽为(n－m)2π，分析时间中心在t＝k、(m－m)处的谐波小波一般表达式。文献[12]证明了谐波小波族ψm，n(t)是一个正交的解析信号，它构成了空间L2(R)的一组正交基。

1.3 谐波小波包

由式(9)可知，谐波小波的关键在于尺度参数m，n的选取。令信号的奈奎斯特频率为fs，则第j(j为非负整数)层各小波的分析频率带宽为：

这样可以设定分析频带的上、下限频率分别为：

随着分解层数j的逐渐增大，可以体现出谐波小波包对信号任意频段的“细化”能力。如果要对信号的某一频段进行重点分析，则先由式(11)确定信号的分解层数j，再由式(12)确定所要分析频带的上、下限频率，也就是定义谐波小波的尺度参数m，n。

由于谐波小波没有尺度函数，因此谐波小波包的思想与传统的小波包理论有所不同，不能采用正交滤波器组对信号进行频带分解。由式(9)可知，谐波小波具有可调的尺度参数m，n，对在不同频带的信号进行分解时采用不同的m，n，这样就可以将谐波小波良好的滤波效果应用到谐波小波包的分析中。信号经过小波包分解后，在各个频带中的信号仍具有与原始信号相同的频率分辨率，而且分解后信号的数据长度并没有减少，这克服了Mallat算法的小波包分解带来数据长度减少的问题。由于小波滤波器不具有理想“盒形”的频谱特性，起始频率和截止频率之间存在过渡带，这导致在信号的分解过程中往往会发生频带间的能量冗余，造成误差，而谐波小波包滤波器则完全可以克服以上问题。具体方法是首先得到待分析信号的频谱，确定谱线的频点数值，然后根据预设的窗宽来确定尺度参数。

2 谐波小波变换及算法

2.1 谐波小波变换

根据小波变换的定义，对某一尺度的小波函数ψm,n(t)，信号z(t)∈L2。(R)的小波变换可表示为：

式(14)和式(15)分别称作信号x(t)在m，n尺度下的时域和频域的谐波小波变换表达式。

对于离散信号序列x(r)，r=0，1，2，…，N-1，其谐波小波变换为：

由式(13)～式(16)可以看出，信号的谐波小波变换非常简洁，容易实现。同时，由于谐波小波对信号各次谐波分量的相位有保持功能，所以对信号进行谐波小波分解后，也可以对信号进行重构，从而实现信号的滤波和降噪。

2.2 谐波小波算法

首先对谐波源信号x(t)进行FFT运算，对变换得到的结果X(ω)进行频率搜索，以确定谐波小波的尺度参数mj，ni，进而确定谐波小波函数hmj,nj(t)，然后将谐波小波函数hmj,nj(t)进行FFT运算的结果Hmj,nj(ω)与X(ω)相乘，再对其相乘的结果W(mj，nj，ω)进行IFFT运算，通过对时域的小波系数W(mj，nj，t)进行重构，得到各次谐波和间谐波的瞬时值，最后利用最小二乘法对各频率分量进行拟合，得到谐波小波分析的结果，其流程图如图2所示。

3 仿真实验与结果分析

为了更好地验证谐波小波算法在电力系统谐波与间谐波分析中的有效性，进行如下的仿真实验。

设电网中的谐波源信号为：

式中：基波频率为50 Hz，并且含有3，5，7，9次谐波和频率为75 Hz(基波频率的1.5倍)的间谐波共6个频率分量以及随机噪声e(t)，具体的参数设置如表1所示。

设采样频率f3＝1 250 Hz，采样点数N＝1 024。利用谐波小波变换(Harmonic：Wavelet Transform，HWT)对谐波源信号μ(t)进行分解，通过Matlab仿真得到分解后各频率分量的波形如图3所示。

由图3可以看出，谐波源中的各次谐波和间谐波分量被分解到了不同的频带中，这表明利用谐波小波算法来实现电力系统谐波和间谐波信号的分离是完全有效的。下一步需要对分解出的各个频带分量进行参数提取，以计算出各次谐波的频率和幅值。

最小二乘法拟合是一个基于全局观念的拟合方法，针对某一样本数据集合，利用该方法可以求得该集合中的主流趋势。利用最小二乘法对6个频带内的谐波和间谐波分量进行拟合，并且定义频率和幅度的误差率分别为：

其计算结果如表2所示。

由表2可以看出，利用HwT法分解并拟合出的各次谐波频率的误差率在10-4量级，幅度的误差率在10-2数量级，完全符合谐波分析的精度要求。由此可见，HwT法在谐波频率和幅值的检测中具有非常明显的优势。

4 结语

将谐波小波引入电力系统的谐波分析中，首先阐述了经典谐波小波及其改进及谐波小波包的概念，接着利用推导出的谐波小波算法对电网中的谐波源信号进行谐波参数提取。仿真结果表明，谐波小波变换可以快速有效地对电力系统中的电压谐波以及间谐波进行检测，并能准确地分解出各次谐波分量。可以预计，随着谐波小波理论的不断发展和完善，谐波小波变换必将在电力系统间的谐波分析中发挥更大作用。