关于机器学习特征选择的方法总结
机器学习特征选择的方法总结
1.特征选择的重要性
随着深度学习的发展， 大大缩减了特征提取和设计的任务。 不过， 特征工程依然是各种机器学习应用领域的重要组成部分。其中对于特征选择(排序)的研究对于数据科学家、机器学习从业者来说非常重要。好的特征选择能够提升模型的性能，更能帮助我们理解数据的特点、底层结构，对进一步改善模型、算法都有着重要作用。
特征选择主要有两个功能：
- 1.减少特征数量、降维，使模型泛化能力更强，减少过拟合
- 2.增强对特征和特征值之间的理解
特征选择的经典经验总结起来主要有三种： 过滤式（Filter）， 封装式（Wrapper）， 集成式（Embedded）。 接下来对这三大类进行详细说明。
2.Filter 过滤式
顾名思义，就是要基于贪心的思想， 把需要的特征筛/滤出来。 一般说来， 基于贪心就需要对特征进行打分。 而这个打分可以基于领域知识， 相关性， 距离，缺失， 稳定性 等等。
2.1 单一特征选择
根据每个特征属性和目标属性之间的计算值来进行排序选择：
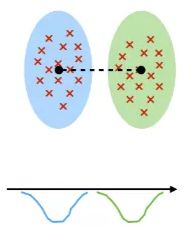
a. Welch’s t-Test： 来判断两个属性的分布的均值方差距离。
t = X ‾ 1 − X ‾ 2 s 1 2 N 1 + s 2 2 N 2 t=\frac{\overline{X}_{1}-\overline{X}_{2}}{\sqrt{\frac{s_{1}^{2}}{N_{1}}+\frac{s_{2}^{2}}{N_{2}}}} t=N1s12+N2s22X1−X2
b. Fish-Score： 和Welch’s t-Test类似， 计算两个分布的距离， 均值只差和方差之和的距离。
S i = ∑ k = 1 K n j ( μ i j − μ i ) 2 ∑ k = 1 K n j ρ i j 2 S_{i}=\frac{\sum_{k=1}^{K} n_{j}\left(\mu_{i j}-\mu_{i}\right)^{2}}{\sum_{k=1}^{K} n_{j} \rho_{i j}^{2}} Si=∑k=1Knjρij2∑k=1Knj(μij−μi)2
c. Chi-Squared test： 计算类别离散值之间的相关性。
χ 2 = ∑ i = 1 r ∑ j = 1 c ( O i , j − E i , j ) 2 E i , j \chi^{2}=\sum_{i=1}^{r} \sum_{j=1}^{c} \frac{\left(O_{i, j}-E_{i, j}\right)^{2}}{E_{i, j}} χ2=i=1∑rj=1∑cEi,j(Oi,j−Ei,j)2
d. Information Gain：计算两个划分的一致性。
I G ( f i , C ) = H ( f i ) − H ( f i ∣ C ) I G\left(f_{i}, \mathcal{C}\right)=H\left(f_{i}\right)-H\left(f_{i} | \mathcal{C}\right) IG(fi,C)=H(fi)−H(fi∣C)
2.2 多特征选择
根据多个特征属性和目标属性之间的计算值来进行排序选择：
e. Relief-F： 根据随机选择的样本点，来计算属性之间的相关性。
S i = 1 2 ∑ k = 1 ℓ d ( X i k − X i M k ) − d ( X i k − X i H k ) S_{i}=\frac{1}{2} \sum_{k=1}^{\ell} d\left(\mathbf{X}_{i k}-\mathbf{X}_{i M_{k}}\right)-d\left(\mathbf{X}_{i k}-\mathbf{X}_{i H_{k}}\right) Si=21k=1∑ℓd(Xik−XiMk)−d(Xik−XiHk)
f. Correlation Feature Selection (CFS)： 利用属性之间的相关性， 进行选择。
3. Wrapper 封装式
通过目标函数来决定是否加入一个变量，就是先选定特定算法，然后再根据算法效果来选择特征集合。 一般会选用普遍效果较好的算法， 例如启发式搜索，完全搜索，随机搜索（GA,SA）等等。
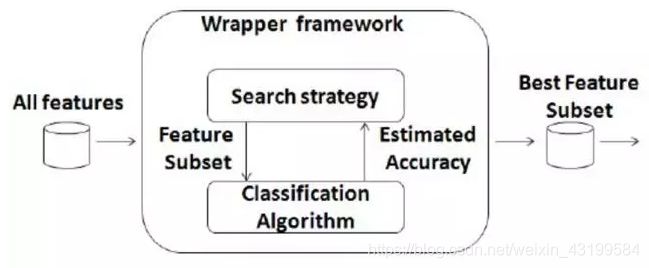这可以使用前面提到的各种减小搜索空间的尝试。 其中最经典的是使用启发式搜索（Heuristic Search）， 而概括的来说主要分为两大类：
g. Forward Selection： 挑出一些属性， 然后慢慢增大挑出的集合。
h. Backward Elimination： 删除一些属性，然后慢慢减小保留的集合。
4. Embedded 集成式
利用正则化思想， 将部分特征属性的权重变成零。 常见的正则化有L1的Lasso，L2的Ridge和混合的Elastic Net。其中L1的算子有明显的特征选择的功能。
在这里面，比较简单的就是会自动进行特征选择， 而且一次性就搞定了， 速度也不错， 难点就是损失函数的选择和缩放参数的选择。
4.1常见的损失函数：
-
Binary(0-1) loss: 灰线 对应错误率
-
Square loss： 紫线 对应最小二乘法
V ( f ( x ⃗ ) , y ) = ( 1 − y f ( x ⃗ ) ) 2 V(f(\vec{x}), y)=(1-y f(\vec{x}))^{2} V(f(x),y)=(1−yf(x))2 -
Hinge loss： 浅蓝 对应 SVM
V ( f ( x ⃗ ) , y ) = max ( 0 , 1 − y f ( x ⃗ ) ) = ∣ 1 − y f ( x ⃗ ) ∣ + V(f(\vec{x}), y)=\max (0,1-y f(\vec{x}))=|1-y f(\vec{x})|_{+} V(f(x),y)=max(0,1−yf(x))=∣1−yf(x)∣+ -
Logistic loss：红线 对应 逻辑回归
V ( f ( x ⃗ ) , y ) = 1 ln 2 ln ( 1 + e − y f ( x ⃗ ) ) V(f(\vec{x}), y)=\frac{1}{\ln 2} \ln \left(1+e^{-y f(\vec{x})}\right) V(f(x),y)=ln21ln(1+e−yf(x))
- Exponential loss：绿线 对应 adaboost
exponential loss ∑ i ϕ ( i , y , f ) = ∑ i e − y i f ( x i ) \text { exponential loss } \sum_{i} \phi(i, y, f)=\sum_{i} e^{-y_{i} f\left(x_{i}\right)} exponential loss i∑ϕ(i,y,f)=i∑e−yif(xi)
4.2 结构化Lasso
除了上述的简单的Lasso，还有结构化的Lasso。
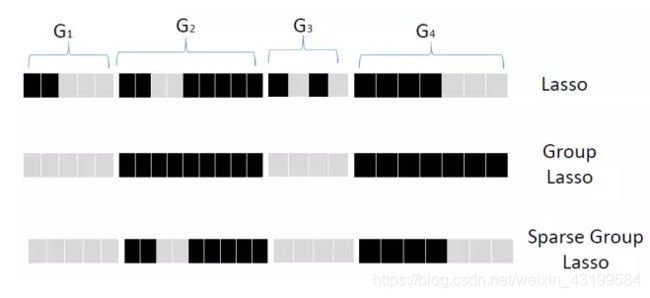
i. Group Lasso： 先将属性进行分组， 然后对每个分组，看成一个属性那样 的采用Lasso的方法选择， 要么全要， 要么全部不要。 再进一步， Sparse Group Lasso再在组内进行选择。
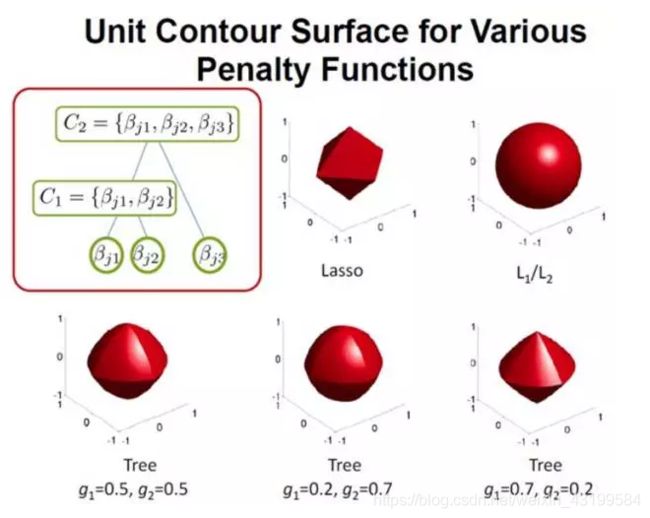
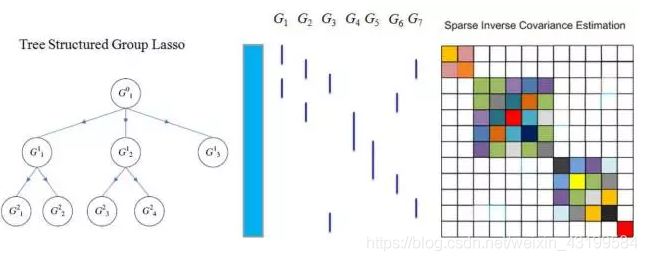
j. Tree-Structured Lasso： 除了前面的扁平（Flat）的结构外， 还有层次化的结构。
对于这种情况， 同样采用类似Group Lasso的思想。 对于一个数的子结构， 要么全要或者全不要，也可以允许分支单独要。
在这种树结构的思想下， 那么每个树的分支的正则化惩罚也可以采用不同的形式。
k. Graph Structure Lasso： 更进一步还可以推广到基于图的Lasso
在图的情况下， 那么两两节点之间要定义一个惩罚项。
penalt y ( w , G ) = λ ∥ w ∥ 1 + ( 1 − λ ) ∑ i , j A i j ( w i − w j ) 2 \text { penalt } y(\mathbf{w}, \mathcal{G})=\lambda\|\mathbf{w}\|_{1}+(1-\lambda) \sum_{i, j} \mathbf{A}_{i j}\left(\mathbf{w}_{i}-\mathbf{w}_{j}\right)^{2} penalt y(w,G)=λ∥w∥1+(1−λ)i,j∑Aij(wi−wj)2
树结构Lasso也可以利用图来表示。
再次强调， 很多时候， 需要综合上面的三种方式来进行综合选择。 特征选择不是一个容易的任务噢。
小结， 特征选择效果好还需要多实战体会的， 下面再简单归纳下：
Filter ：
优点： 快速， 只需要基础统计知识。
缺点：特征之间的组合效应难以挖掘。
Wrapper：
优点： 直接面向算法优化， 不需要太多知识。
缺点： 庞大的搜索空间， 需要定义启发式策略。
Embedded：
优点： 快速， 并且面向算法。
缺点： 需要调整结构和参数配置， 而这需要深入的知识和经验。
参考内容：
http://www.rokkincat.com/blog/2016/04/28/feature-selection
https://mp.weixin.qq.com/s/TRgaqpokbNHXKS0E2Lz78A
http://www.denizyuret.com/2014/02/machine-learning-in-5-pictures.html