（新型事件相机有关的论文解读）Unsupervised Event-based Learning of Optical Flow, Depth, and Egomotion

新型事件相机有关的论文解读之：

Unsupervised Event-based Learning of Optical Flow, Depth, and Egomotion

关于事件相机：
事件相机是一个新型的类脑相机，是一个待开发的大领域。希望通过我的分享，能够有更多人来研究并将它更好地运用在我们的生活中~
对于事件相机还不了解的朋友们可以看我这一系列的另一篇博客：事件相机（Event Camera）及相关研究简介——新一代相机？新的计算机视觉领域？

本篇论文地址：https://arxiv.org/abs/1812.08156v1
作者在youtube上上传了项目视频：https://www.youtube.com/watch?v=aDzFSG4yV0M&t=1078s

写在前面

这篇论文做的工作不止有光流估计，还有深度和姿态的估计。
这篇论文和我之前分享的EVFlowNet非常相似，可以说是EVFlowNet的改进版，两篇论文的作者也相同（膜Alex大佬）。之前在另一篇文章解读的博客里（A Unifying Contrast Maximization Framework for Event Cameras）也提到过这篇论文，这篇论文的部分设计思路也来源于那篇。
在EVFlowNet介绍的结尾，我说到目前这类算法的局限性。人们更希望去寻找无监督的，不使用灰度图的方法，以此来证明事件相机的优越性。这篇论文就是一个全无监督的网络，也没有了灰度图的参与。

贡献

1、一种新的离散事件量表示方法，用于将事件传递到神经网络中。
2、一个新颖的应用运动模糊为基础的损失函数，来做到仅使用事件的无监督学习。
3、一种新的立体相似性损失在去模糊事件图像普查变换中的应用。
4、在MVSEC上的定量测试，同时定性定量地在多种夜晚环境下进行测试。

下面我们来一一讲解

网络结构

论文使用的网络结构如图，可以看到其结构和EVFlowNet几乎相同，loss计算位置的细节也几乎相同，在这里不多叙述，大家可以转到我对EVFlowNet介绍的博客中去了解。
在进行光流预测时，网络为普通的Encoder+Decoder结构，在进行深度和姿态估计时，Encoder+Decoder结构用于估计深度，而上图中的pose_model（紫色部分）用于输出姿态估计。

事件如何放入网络

如何将事件信息转化为图像或放入网络结构里是很多人研究的点，也是事件视觉领域相比于rgb视觉领域的一个难点。在EVFlowNet里，作者将两幅灰度图之间的事件累积在一个四通道的图片上，前两通道为事件数累积（count_image），后两通道为最近的事件时间（time_image）。在本篇论文里，作者又提出了一种新的方法。
假设一次前向传播中输入的事件数为N，这列事件为$\{(x_i,y_i,t_i,p_i){\}}_{i\in [1,N]}$，然后我们将这一列事件划分为离散的B个容器里。将时间尺度转到[0,B-1]上，并对事件进行下列操作：

其中$k_b(a)$类似于一个双线性采样核函数。由于相机失真的矫正可能导致像素对应的坐标变成浮点数，所以应该使用该插值函数计算出原来整数坐标下像素应有的值。
通过这样的操作，就将输入的事件分为了B组。

姿态补偿

所谓姿态补偿通常通俗点说也就是去模糊吧，就是通过计算相机的姿态，把一个组里的所有不同时刻的事件通过姿态变换转到同一时间戳上，这样能使得图像模糊最小。
这里假设u、v为每个像素的光流，根据光流的定义，我们可以把所有的事件坐标$(x_i,y_i)$变换到统一时间戳$t^{\prime }$时它应该处于的坐标$(x_i^{\prime },y_i^{\prime })$。可想而知，变换后的坐标是浮点数。

这样的操作是否成功进行了姿态补偿，在于光流值是否准确，那么如何判定其是否准确呢，这里作者尝试使用了文章（A Unifying Contrast Maximization Framework for Event Cameras）中的方法，计算变换后事件数的方差作为loss，但他发现这样的方法非常容易过拟合。之后，作者运用了另一篇文章中提到的方法：最小化时间图像和。
为什么这样做呢，可以想象，如果光流估计的准确的话，所有事件将被变换到在$t^{\prime }$时刻它们本来所处的位置，那么事件将会大概率重叠，逐像素地计算其上事件的平均时间戳，再将其求和，这个值将会较小。而如果光流估计不正确，那么事件可能会更加混乱，重叠的事件数较少，逐点计算其上事件的平均时间再求和，这个值会很大。形象地举个例子就是下面这样：
$$2+3+4+5>\frac{1+2}{2}+\frac{3+4}{2}$$
那么下来就是它的数学表示了：

这里$k_b(x)$仍为之前定义的双线性采样核函数。由于如果直接将变换后的浮点坐标四舍五入，将引入不可微的取整函数，导致网络无法训练，所以这里采用了类似于双线性采样的方式，将一个浮点坐标对应的像素值按距离比例分配到其周围的四个整数坐标的点上，如下图：

公式中$p^{\prime }$控制事件极性，也就是说正负事件分开计算。然后在求和时候逐点求正负事件平均时间戳的平方和。

这样，能够衡量光流估计准确与否的时间误差（time_loss）就计算完成了。
在设计完成后，还有一个问题：统一时间$t^{\prime }$怎么确定。自然地我们想到用输入的所有事件中时间最小的，即最初的事件时间。但是这里就会有一个问题，与这个事件时间上靠的近的事件在反向传播的时候会乘一个$(t^{\prime }-t_i)$的项，这个项可能会非常小导致梯度消失。所以作者设定了两个$t^{\prime }$，分别计算，最后相加，这两个$t^{\prime }$为所有事件时间中的最大值与最小值，即最初时刻与最末时刻，用$t_1$与$t_N$表示，公式如下：

这样，我们就可以用一个损失函数$L_{time}$来衡量姿态补偿是否完成。

光流估计

在上面姿态补偿部分的叙述中，我们便可以通过损失函数$L_{time}$训练做到姿态补偿。同时，姿态补偿时候的u、v恰好就是光流，所以，同样适用类似的损害函数便可以进行光流估计。
与EVFlowNet类似，除了$L_{time}$外还要加一个正则项$L_{smooth}$，即光滑损失。因为输出的光流图应该是空间上光滑的，相邻像素之间的光流不应该差别很大。所以该损失定义为每个像素的光流与其周围的像素上的光流之间的差距的和。

与一般论文类似，这里的$N(x)$表示向量x的邻居们，这里定义为其四邻居。函数$\rho$表示Charbonnier损失函数，其定义为：
$$\rho (x)=\sqrt{x^2+{ϵ}^2}$$
其中$ϵ$为一个较小的常数，防止x在接近零的时候反传变得奇怪~
这样，在做光流估计时的损失函数定义为：

姿态和深度估计

这里要说明一下，光流是用一套参数估计的，而深度和姿态是用另一套参数估计的。也就是说网络结构相似，分开训练两类任务。

重映射误差

为了导出重映射误差，我们将光流与相机参数和姿态之间的关系写出来，如下：

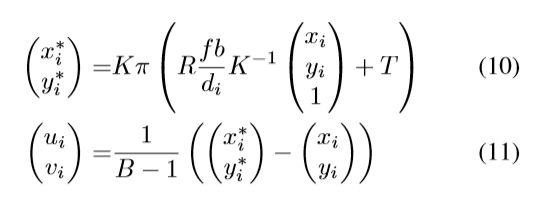
这个公式很好理解，就是基本的三维空间的变换。u、v为光流，K为相机内参，R为旋转矩阵，T为平移向量，$\pi$为透视函数，f为相机焦距，b为双目的基线长度。
由于上面已经有了评判光流准确有否好损失，故将这里得到的光流带入上面的损失中即可判断R矩阵估计的准确与否，最终我们可以从估计准确的R矩阵中导出欧拉角$(\psi ,\beta ,\varphi )$
这里的误差记为$L_{temporal}$

立体视差

这里立体视差输入的是通过上述计算到的光流去模糊后的图片，是基于census变换来设计的。因为即使是同一时刻的图像，左右的事件数也可能不一样，所以直接使用光度误差会不太友好，而census变换对亮度并不敏感，所以作者采用了它。
在同一时刻，左右两个相机的图像应该是相似的，如果把视差计算进去那左右图应该是相同的。所以我们利用网络最后输出的左图片的视差，将右图片的census变换warping到左图上，然后计算两者之间的差距，这里和上面一样使用Charbonnier损失。同样的，反过来对右图片计算一次。这一项我们记为$L_{stereo}$。
另外，作者还设计了$L_{consistency}$，在同一时刻，左右输出的视差应该相似，所以这一项代表左右视差的差值。
最后总的损失表示为：

这里$L_{smoothness}$与上面光流预测部分相同。
下来就是无尽的调参了吧。。

个人总结

这篇文章最后的结果还不错，部分的准确率提升了很多，是在事件视觉领域尝试无监督方式的一大步。同时相似的论文还有很多，这些论文或是在改变结构，或是在设计前端，又或是在尝试设计损失。总之，在事件视觉领域，这些都是有待开发的方面。如何设计前端可以把事件信息巧妙的输入网络？如何设计网络能够最大程度地提取事件中蕴藏着的我们所需要的信息？同时去除噪声和无用信息。如何设计损失能够使网络更好地训练，无监督地训练？