膨胀卷积/空洞卷积以及如何处理gridding effect问题

膨胀卷积

如图:左边为普通卷积，右边为膨胀卷积，右图中的r为膨胀因子，r=2表示卷积核是有间隙的，间隔为r-1 = 1也就是间隔一个空格

膨胀卷积作用：

增大感受野

保持输出特征尺寸不变

使用膨胀卷积的原因：

在语义分割中，我们通常会将分类网络作为网络Backbone,通过网络backbone会对图片进行一些的下采样，然后输出后会对特征图进行上采样，但是往往因为下采样倍数太大，通过maxpooling层会损失很多细节信息，通过单单上采样还原也达不到很好的效果。列如在VGG16网络中会下采样32倍，这时有人会想为什么不能去掉maxpooling层，这样特征图片尺寸就不会变了，但这样会使感受野变小，实际上maxpooling层有着增大感受野的作用。这时就可以体现出膨胀卷积的作用了。

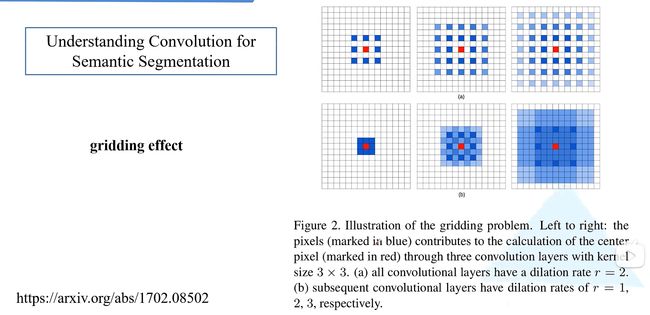
但堆叠膨胀卷积会引起“gridding effect”问题，（如下图）：

什么是“gridding effect”问题？

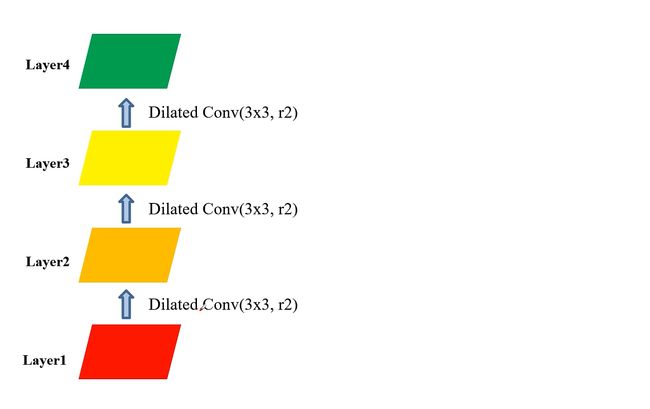
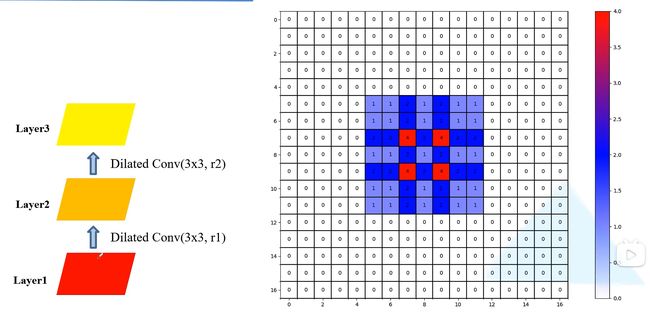
一、实验一

如上图假设我们使用三个膨胀卷积对特征图进行操作，卷积核大小都为3*3，膨胀系数都为2

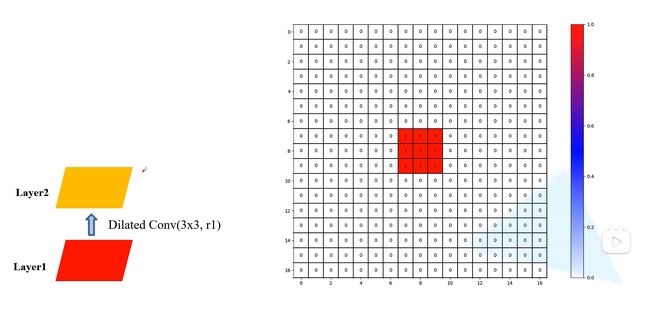
Layer1——Layer2

如下图在layer2上，我们看一下在这一层用到了layer1上的哪一些数据，对于layer2上的每一个像素会使用layer1上9个膨胀卷积形状的像素

Layer1——Layer2——Layer3

如下图，经过计算可以看到layer3上的每一个元素利用到的layer1层上的像素，数字表示计算过程该位置像素参与计算的次数，举例：例如图中最中心的9这个数字，可以表示为了得到layer3上特征图，得到9所在的位置的像素预测值，9本身这个位置的像素会参与9次计算，膨胀卷积利用到的原图也就layer1层的像素分布如图所示。

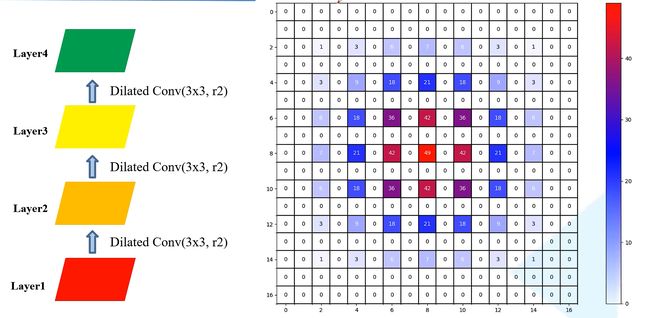
Layer1——Layer2——Layer3——Layer4

如下图，layer4用到的layer1像素次数分布，这时会发现在这个范围内有0行，也就是说最终得到的9这个位置的像素预测值并没有用到这个范围内的所有像素，这就成为“griddingeffect”现象，这会导致最后的特征图丢失一些细节上的信息。

那么如何避免“gridingeffect”现象？

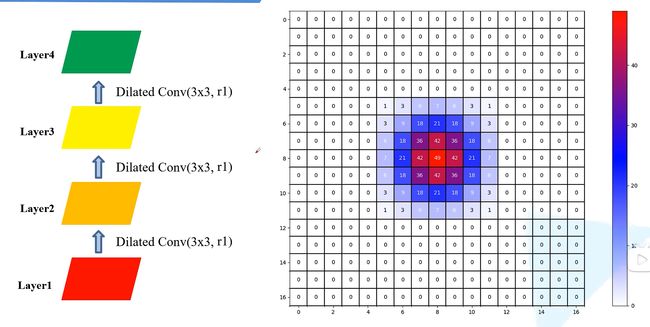
二、实验二

我们先看另一种膨胀系数的情况，这里把膨胀系数设为1，2，3

Layer1——Layer2

如下图在layer2上，我们看一下在这一层用到了layer1上的哪一些数据，对于layer2上的每一个像素会使用layer1上9个膨胀卷积形状的像素，这里膨胀系数为1，所以就是普通卷积。

Lay1——Lay2——Lay3

同理，如下图，经过计算可以看到layer3上的每一个元素利用到的layer1层上的像素，数字表示计算过程该位置像素参与计算的次数，举例：例如图中4这个数字，可以表示为了得到layer3上特征图，得到4所在的位置的像素预测值，4本身这个位置的像素会参与4次计算，膨胀卷积利用到的原图也就layer1层的像素分布如图所示。

Layer1——Layer2——Layer3——Layer4

可以看到最终感受野是13*13，数字的解释和上面类似，在这里，参数都有被用到，没用0行间隙，与上面使用3个膨胀系数为2的卷积相比，感受野一样，卷积核参数也一样。

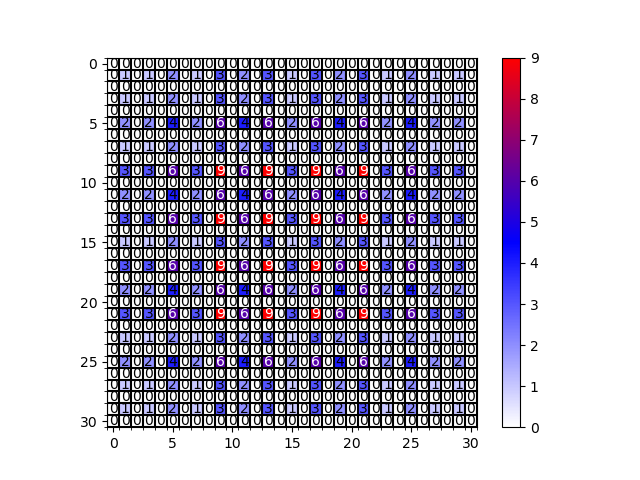
三、实验三

我们再看一种情况假设我们这次使用3个普通卷积，也即膨胀系数为1的卷积，相关具体不再赘述，下面为结果图

Layer1——Layer2

Lay1——Lay2——Lay3

Layer1——Layer2——Layer3——Layer4

可以看到参数数量一样，因为都是3*3的卷积核，但感受野更小为7*7，由此我们得到使用膨胀卷积可以在参数相同的情况下，扩大感受野

设置膨胀系数

原论文膨胀系数设置分析

建议一

如上图，作者给出了设置连续膨胀卷积的膨胀系数准则：

假设我们有N个K*K的膨胀卷积层，它们对应的膨胀系数为[r1,r2,r3,…rn],我们要避免gridding effect问题，作者这样定义：

ᵄ0ᵅ6=maxᵄ0ᵅ6+1 −2ᵅfᵅ6,ᵄ0ᵅ6+1 −2ᵄ0ᵅ6+1 − ᵅfᵅ6,ᵅfᵅ6

这个公式表示对于第i层两个非零元素最大距离，ᵄ0ᵅ6为第i层的两非零元素的最大距离，ᵅfᵅ6为第i层的膨胀系数，对于最后一层Mn非零元素最大距离为rn,目的是为了让M2

举例：

当卷积核大小为3 * 3也即K= 3，设置r = [1,2,5]这时M3 = r3 = 5,M2 = max[M3 - 2 * 2,M3 - 2(M3 - 2),2] = [1,-1,2] = 2< 3

再看同样K= 3，r = [1,2,9],M3=9,M2 = max[M3 - 2 * 2,M3 - 2(M3 - 2),2] =[5,-5,2] = 5 > 3

我们可以用代码来验证以下是不是[1,2,5]是不会有griddingeffect 问题，[1,2,9] 是不是存在gridding effect 问题

代码验证

r =[1,2,5]

r =[1,2,9]

可以看到[1,2,5]没有griddingeffect 问题，[1,2,9] 存在gridding effect 问题

代码地址：deep-learning-for-image-processing/main.py atmaster · WZMIAOMIAO/deep-learning-for-image-processing (github.com)

建议二

论文中建议将膨胀系数设置为锯齿结构

建议三

膨胀系数公约数不能大于1

例如r = [2 ,4，8]时，存在“graddingeffect”

结果比较

如图，第一行为groundtruth第二行为没有采用这个这个HDC设计准则第三行采用了HDC这个准则，可以看到效果还是很好的。

参考视频：膨胀卷积(Dilatedconvolution)详解_哔哩哔哩_bilibili

代码地址：

https://github.com/WZMIAOMIAO/deep-learning-for-image-processing/tree/master/others_project/draw_dilated_conv