SORT：SIMPLE ONLINE AND REALTIME TRACKING

本文对经典的SORT方法原文进行翻译，便于加深原理理解和代码实现。

0. 摘要

本文探讨了一种实用的多目标跟踪方法，其主要重点是为在线和实时应用中有效地关联（associate）目标物。为此，检测质量是影响跟踪性能的关键因素，更改检测器可以将跟踪质量提高多达18.9％。 尽管只是使用了诸如卡尔曼滤波（Kalman Filter）和匈牙利算法（Hungarian algorithm）之类的的初级组合，但该方法仍达到与SOTA（state-of-the-art）在线跟踪器相当的精度。 此外，由于我们设计的这种跟踪方法的简易性，该跟踪器的更新频率为260 Hz，比其他最新的跟踪器快20倍以上。

关键词 - 计算机视觉，目标跟踪，检测，数据关联

1. 引言

本文针对多目标跟踪（MOT）问题提出了一种基于检测的跟踪（tracking-by-detection）框架的实现方式，在该问题中，每帧都检测到多个目标并将其表示为边界框（Bounding Box）。与许多基于批处理（batch based）的跟踪方法[1,2,3]相比，本文的工作主要针对在线跟踪（online tracking），即仅基于前一帧和当前帧的检测结果来进行跟踪。此外，研究的重点放在效率上，这有利于实时跟踪，同时促进诸如自动驾驶汽车对行人跟踪之类的应用。

MOT问题可以看作是数据关联问题（association problem）,其目的是将视频序列中不同帧的检测关联起来。为了助于数据关联过程，跟踪器使用各种方法对场景中目标物的运动[1,4]和外观[5,3]进行建模。本文提出的方法受最近确立的视觉MOT 基准(benchmark)[6]获得启发而实现。

首先，日趋成熟的数据关联技术，其中包括多重假设跟踪(Multiple Hypothesis Tracking)(MHT)[7,3]和联合概率数据关联(Joint Probabilistic Data Association))JPDA)[2]，这两类占据了MOT benchmark的许多Top位置。

其次，唯一不使用聚合通道滤波器(Aggregate Channel Filte)的跟踪器也是排名最高的跟踪器，这表明检测质量的好坏拉低了其他跟踪器的排名，也就是说检测质量对跟踪结果产生了至关重要的影响。

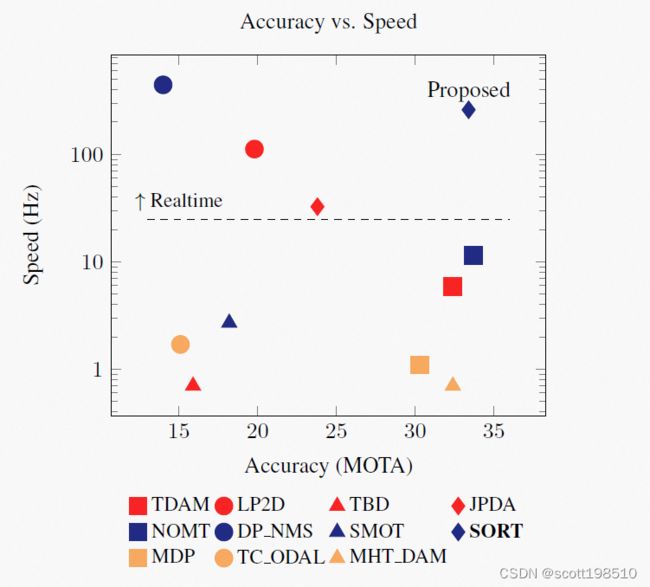
此外，精度和速度之间的权衡似乎非常明显，因为对于实时应用而言，最精确的跟踪器的速度被认为太慢了（见图1）。随着top级的在线和批处理跟踪器之中使用传统数据关联技术的兴起，以及top级跟踪器所使用的各种不同检测方法，本项工作探索了MOT可以做到如此简单同时其性能依然强大。

根据奥卡姆剃刀原理（“非必要，勿增加”，即“简单有效原理”），跟踪时会忽略检测目标的外观特征，并且仅将边界框的位置和大小用于运动估计和数据关联。 此外，关于短期和长期遮挡（occlusion）的问题也可以被忽略，因为这类问题很少发生，并且对它们的显式处理会引入不必要的复杂性到跟踪框架中。因此我们认为，以目标重识别的形式引入复杂性会大大增加跟踪框架的计算开销，这可能会限制其在实时应用中的使用。

这种设计理念与许多视觉跟踪器形成了鲜明的对比，那些视觉跟踪器结合了无数组件来处理各种边缘情况和检测错误[9,10,11,12]。与之相反，我们这项工作着重于有效且可靠地处理常见的帧间关联。相比于专注鲁棒性的检测错误，我们选择利用目标检测器的最新进展直接解决检测问题。通过将常见的ACF行人检测器[8]与最近基于卷积神经网络（CNN）的检测器[13]进行比较，可以证明这一点。 此外，采用了两种经典而又极为有效的方法，即卡尔曼滤波器[14]和匈牙利算法[15]来分别处理跟踪问题的运动预测和数据关联问题。 跟踪的这种简化形式提高了在线跟踪的效率和可靠性，参见图1。在本文中，此方法仅适用于跟踪各种环境中的行人，但是由于CNN检测器的灵活性[13]，因此很自然可以推广到跟踪其他类型的目标。

本文的主要贡献是：

• 我们利用基于CNN的检测能力解决MOT场景问题；

• 提出了基于卡尔曼滤波器和匈牙利算法的实用跟踪方法，并在最新的MOT基准上进行了评测；

• 代码将开源，以帮助建立用于研究的baseline和避免应用过程中产生不必要的冲突或纠纷。

本文的结构安排如下：

• 第2部分简要介绍了多目标跟踪领域的相关文献

• 第3部分介绍了我们提出的跟踪框架

• 第4部分中验证了该框架在一系列benchmark上的有效性。

• 第5部分对本项研究进行了总结并讨论了未来的改进方向。

2. 文献回顾

传统上，使用多重假设跟踪(MHT)[7]或联合概率数据关联(JPDA)滤波器[16,2]来解决MOT问题，但这在目标分配不确定的情况下，会延迟做出困难的决策。 这些方法的组合复杂度随跟踪目标的数量增加呈指数级增长，这使得其在高动态环境的实时应用中根本不切实际。最近,Rezatofighi等人[2] 重新探讨了视觉MOT中的JPDA公式[16]，其目标是通过利用整数规划的最新研究来解决JPDA的有效近似问题。 同样，Kim等[3]为每个目标使用了外观模型来修剪MHT图，以实现最新的性能。但是，这些方法仍会做出延迟的决策，因此不适宜用于在线跟踪。

许多在线跟踪方法旨在通过在线学习(online learning)建立单个目标本身的外观模型(appearance models)[17,18,12]或全局模型(global model)[19,11,4,5]。除外观模型外，还经常嵌入运动以协助将检测与 tracklets 相关联[1,19,4,11]。当仅考虑建模为二分图匹配(bipartite graph matching)的一一对应时，可以使用诸如匈牙利算法[15]之类的全局最优解[10,20]，在多目标跟踪问题中可以简单理解为寻找前后两帧的若干目标的匹配最优解的一种算法。

Geiger等人的方法[20]在两阶段中使用匈牙利算法[15]。 首先，通过将相邻帧之间的检测关联起来形成小段轨迹，在该相邻帧中，将几何形状和外观特征结合在一起以形成关联矩阵（affinity matrix）。然后，再次利用几何和外观特征形成的各小段轨迹彼此关联起来以桥接因遮挡引起的折断轨迹。 这种两步关联法限制了该方法无法用于批处理计算。 我们提出的方法受[20]提出的跟踪器组件而启发，但是我们将关联过程简化为单个步骤，正如下一节所述。

3. 方法

所提出的方法包含：目标检测，将目标状态传播到下一帧，将当前检测目标与现有目标相关联，同时管理跟踪目标的生命周期。

3.1. 检测器

为了利用快速发展的基于CNN的检测技术，我们利用了Faster Region CNN（FrRCNN）检测框架[13]。 FrRCNN是一个包含两个阶段的端到端框架。第一阶段提取特征并为第二阶段提出区域(regions)，然后在提出的区域中分类出目标。该框架的优势在于，两个阶段之间共享参数，从而创建了一个有效的检测框架。 此外，网络架构本身可以替换为任何其他网络设计，从而可以对不同的架构进行快速试验以提高检测性能。

在这里，我们比较了FrRCNN提供的两种网络体系结构，即Zeiler、Fergus的体系结构(FrRCNN（ZF))[21]和更深层次的Simonyan、Zisserman的体系结构(FrRCNN(VGG16))[22]。 在整个工作过程中，我们将带有默认参数的FrRCNN用于PASCAL VOC。由于我们仅对行人感兴趣，因此忽略了所有其他类别的判断，仅将行人检测输出概率大于50％结果传递给跟踪框架。

通过切换检测器来比较跟踪性能。 评估验证结果如下：

在我们的实验中，我们将FrRCNN检测与ACF检测进行比较时，发现检测质量对跟踪性能有重大影响，作用于现有的在线跟踪器MDP [12]和本文提出的跟踪器的一系列验证集可以佐证这一点。 表1结果表明，对于MDP和本文的方法，最佳检测器(FrRCNN(VGG16))展示了最佳的跟踪精度。

3.2. 估计模型

在这一节，我们描述了目标模型，用于将目标的ID传播到下一帧的表示形式和运动模型。我们使用线性匀速模型(linear constant velocity model)来估计每个目标的帧间位移，该模型与其他目标和相机运动无关。 每个目标的状态建模为：

其中分别代表目标中心的水平和垂直坐标，而比例分别代表目标边框的尺寸和长宽比。注意,长宽比被认为是恒定的。当检测与目标相关联时，检测到的边界框将用于更新目标状态，在该状态下通过卡尔曼滤波器对速度分量进行最佳求解[14]。 如果没有检测与目标相关联，则无需进行校正，直接使用线性速度模型即可简单预测其状态。

3.3. 数据关联

在将检测结果分配(assign)给现有目标时，通过预测其在当前帧中的新位置来估计每个目标的边界框几何形状。然后，分配成本矩阵(assignment cost matrix)计算为每个检测结果与现有目标的所有边界框之间的交并比(IOU)距离(IOU distance)。使用匈牙利算法可以最佳解决分配问题。 另外，如果目标检测重叠度小于，则将施加最低IOU来拒绝分配。

我们发现边界框的IOU距离隐式处理了目标引起的短期遮挡。 具体来说，当目标被遮挡物覆盖时，由于IOU距离恰好有利于具有类似比例的检测，因此仅检测到遮挡物。 这允许通过检测对两个遮挡目标进行校正，而被覆盖的目标未被分配也不受影响。

简单来说就是使用IOU来计算cost矩阵，是能隐式地缓解遮挡问题。在遮挡过程中仅检测到前方的遮挡物，无法检测到后方被遮挡的目标，而大小相近的物体间的IOU是较大的，那么可以把遮挡物和原目标进行关联，在遮挡结束后再恢复正确的关联。

3.4. 创建和删除Track Identities

当目标进入和离开图像时，需要相应地创建或销毁唯一标识ID。 对于创建跟踪器，我们认为任何重叠小于 的检测结果都表示未被跟踪的目标。使用速度设置为零的边界框来初始化跟踪器。 由于此时未观察到速度，因此将速度分量的协方差初始化为较大的值，从而反映出这种不确定性。 此外，新的跟踪器会经历一个试用期，在此期间，目标需要与检测器相关联足够多次，以积累足够的evidence预防假阳性的检测结果。

如果有 帧未检测到目标，则将终止对他的跟踪。 这可以防止在没有对检测器校正的情况下，由于长时间的预测而导致的跟踪器数量的无限增长和定位错误。 在所有实验中，出于两个原因，将设置为1。 首先，匀速模型不能很好地预测真实的动力学，其次，我们主要关注帧到帧的跟踪，而目标的重新识别超出了本文的范围。 此外，及早删除丢失的目标有助于提高效率。如果目标物再次出现，将以新的身份ID对他跟踪。

4. 实验

我们根据MOT基准数据库[6]设置的一系列测试集评估跟踪器的性能，该数据库包含移动摄像机和静态摄像机拍摄的视频流。 为了调整初始卡尔曼滤波器的协方差，和 ，我们使用与[12]中相同的训练集、验证集拆分方式。 使用的检测架构是FrRCNN(VGG16)[22]。[22]中检测器的源代码和样本可以在线获取。

4.1. Metrics

由于很难使用单一的评分来评估多目标跟踪性能，因此我们利用[24]中定义的评测指标以及标准的MOT指标[25]：

• MOTA(↑): 多目标跟踪 accuracy [25]；

• MOTP(↑): 多目标跟踪 precision [25]；

• FAF(↓): 每帧错误警报的数量；

• MT(↑): 大多数跟踪的轨迹数。 即目标在至少80％的生命周期中具有相同的标签；

• ML(↓): 大部分丢失的轨迹数。 也就是说，至少在其生命周期的20％内未跟踪目标；

• FP(↓): 错误检测的次数；

• FN(↓): 丢失的检测次数；

• ID sw(↓): ID切换到另一个先前跟踪的目标的次数[24]；

• Frag(↓): 跟踪被误检测中断的碎片数。

带有（↑）的评测指标，分数越高表示性能越好； 对于（↓）的评估指标，分数越低表示性能越好。真阳性代表跟踪边界框与相应的 ground truth 边界框至少有50％重叠。 评测代码可以从[6]下载。

4.2. 性能评测

使用MOT benchmark[6]评估跟踪性能，ground truth保留11个序列的基本情况。 表2将本文的方法SORT与其他几种基baseline跟踪器进行了比较。 为简洁起见，只有最相关的跟踪器(就准确性而言是最先进的在线跟踪器)，例如(TDAM [18]，MDP [12])，最快的基于批处理的跟踪器(DP NMS [23]))，并列出了所有近似在线方法(NOMT [11]))。 此外，还列出了启发本文方法的方法(TBD [20]，ALEXTRAC[5]和SMOT [1])。与其他方法相比，SORT获得了在线跟踪器的最高的MOTA评分，并且可以与最先进的方法NOMT相提并论，而后者明显更复杂并且在不久的将来会使用框架。 另外，由于SORT的目标是专注于帧与帧之间的关联，因此尽管具有与其他跟踪器类似的误报(False Negative），但丢失的目标(ML)的数量最少。 此外，由于SORT专注于帧到帧的关联形成小段轨迹，因此与其他方法相比，它丢失的目标数量最少。

4.3. 运行耗时

大多数MOT解决方案为了得到更高的跟踪准确性，多是以牺牲运行时间为代价。虽然离线处理任务中可以允许缓慢的运行处理，但对于机器人技术和自动驾驶汽车，实时性能至关重要。 图1显示了MOT基准[6]上的许多跟踪器，这些跟踪器的速度和准确性都很高。 这表明达到最佳准确性的方法也往往是最慢的（图1右下）。在图的另一端，最快的方法往往具有较低的检测准确性（图1的左上角）。SORT没有明显的不足，它并结合了理想的速度和准确性（图1右上方）。 跟踪器在具有16 GB内存的Intel i7 2.5GHz计算机的单核上以260 Hz的频率运行。

5. 结论

在本文中，提出了一个简单的在线跟踪框架，该框架着重于帧间预测和关联。我们验证了跟踪质量高度依赖于检测性能，并且通过利用检测器的最新成果，仅采用经典跟踪方法就可以实现最佳的跟踪质量。 所提出的框架在速度和准确性方面都达到了同类最佳的性能，而其他方法通常会牺牲某些性能。 本文框架的简单性使其非常适合作为baseline，来研究在长期遮挡的情况下重识别目标的方法。 由于我们的实验突出了检测质量在跟踪中的重要性，因此未来的工作将研究检测和跟踪的紧耦合框架。

6. 参考文献

[1] C. Dicle, M. Sznaier, and O. Camps, “The way they move: Tracking multiple targets with similar appearance,” in International Conference on Computer Vision,2013.

[2] S. H. Rezatofighi, A. Milan, Z. Zhang, A. Dick, Q. Shi, and I. Reid, “Joint Probabilistic Data Association Revisited,” in International Conference on Computer Vision,2015.

[3] C. Kim, F. Li, A. Ciptadi, and J. M. Rehg, “Multiple Hypothesis Tracking Revisited,” in International Conference on Computer Vision, 2015.

[4] J. H. Yoon, M. H. Yang, J. Lim, and K. J. Yoon,“Bayesian Multi-Object Tracking Using Motion Context from Multiple Objects,” in Winter Conference on Applications of Computer Vision, 2015.

[5] A. Bewley, L. Ott, F. Ramos, and B. Upcroft, “ALExTRAC: Affinity Learning by Exploring Temporal Reinforcement within Association Chains,” in International Conference on Robotics and Automation. 2016, IEEE.

[6] L. Leal-Taix´e, A. Milan, I. Reid, S. Roth, and K. Schindler, “MOTChallenge 2015: Towards a Benchmark for Multi-Target Tracking,” arXiv preprint, 2015.

[7] D. Reid, “An Algorithm for Tracking Multiple Targets,”Automatic Control, vol. 24, pp. 843–854, 1979.

[8] P. Dollar, R. Appel, S. Belongie, and P. Perona, “Fast Feature Pyramids for Object Detection,” Pattern Analysis and Machine Intelligence, vol. 36, 2014.

[9] S. Oh, S. Russell, and S. Sastry, “Markov Chain Monte Carlo Data Association for General MultipleTarget Tracking Problems,” in Decision and Control.2004, pp. 735–742, IEEE.

[10] A. Perera, C. Srinivas, A. Hoogs, and G. Brooksby,“Multi-Object Tracking Through Simultaneous Long Occlusions and Split-Merge Conditions,” in Computer Vision and Pattern Recognition. 2006, IEEE.

[11] W. Choi, “Near-Online Multi-target Tracking with Aggregated Local Flow Descriptor,” in International Conference on Computer Vision, 2015.

[12] Y. Xiang, A. Alahi, and S. Savarese, “Learning to Track: Online Multi-Object Tracking by Decision Making,”in International Conference on Computer Vision, 2015.

[13] S. Ren, K. He, R. Girshick, and J. Sun, “Faster R-CNN:Towards Real-Time Object Detection with Region Proposal Networks,” in Advances in Neural Information Processing Systems, 2015.

[14] R. Kalman, “A New Approach to Linear Filtering and Prediction Problems,” Journal of Basic Engineering, vol. 82, no. Series D, pp. 35–45, 1960.

[15] H. W. Kuhn, “The Hungarian method for the assignment problem,” Naval Research Logistics Quarterly, vol. 2,pp. 83–97, 1955.

[16] Y. Bar-Shalom, Tracking and data association, Academic Press Professional, Inc., 1987.

[17] S. H. Bae and K. J. Yoon, “Robust Online Multi-Object Tracking based on Tracklet Confidence and Online Discriminative Appearance Learning,” Computer Vision and Pattern Recognition, 2014.

[18] Y. Min and J. Yunde, “Temporal Dynamic Appearance Modeling for Online Multi-Person Tracking,” oct 2015.

[19] A. Bewley, V. Guizilini, F. Ramos, and B. Upcroft,“Online Self-Supervised Multi-Instance Segmentation of Dynamic Objects,” in International Conference on Robotics and Automation. 2014, IEEE.

[20] A. Geiger, M. Lauer, C. Wojek, C. Stiller, and R. Urtasun, “3D Traffic Scene Understanding from Movable Platforms,” Pattern Analysis and Machine Intelligence,2014.

[21] M. Zeiler and R. Fergus, “Visualizing and Understanding Convolutional Networks,” in European Conference on Computer Vision, 2014.

[22] K. Simonyan and A. Zisserman, “Very Deep Convolutional Networks for Large-Scale Image Recognition,” in International Conference on Learning Representations, 2015.

[23] H. Pirsiavash, D. Ramanan, and C. Fowlkes, “Globallyoptimal greedy algorithms for tracking a variable number of objects,” in Computer Vision and Pattern Recognition. 2011, IEEE.

[24] Y. Li, C. Huang, and R. Nevatia, “Learning to associate: HybridBoosted multi-target tracker for crowded scene,” in Computer Vision and Pattern Recognition.2009, IEEE.

[25] K. Bernardin and R. Stiefelhagen, “Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics,” Image and Video Processing, , no. May, 2008.

SORT 目标跟踪算法源码分析

SORT/Deep SORT 物体跟踪算法解析

7.算法理解与源码分析

在分析具体源码前，主要理解以下三个相关算法。

1. IoU的计算如下图所示，本质上是计算两部分的重叠面积与两部分并集的比值，当完全重叠时为1，完全不相交时为0.

2. 匈牙利算法解决分配问题

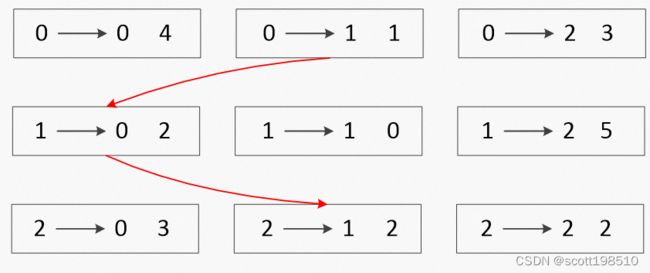
在源代码中直接使用的linear_sum_assignment，本质上是一个线性规划问题，其理解过程如下：

矩阵对应的是cost 矩阵，对应的是第 i 个分裂点对应的顶点为j，具体来说好比第i个人分配第j份工作，对应的需要的代价，如果就是 m个人分配n 份工作的代价函数计算。

一个简单的例子就是如下的cost 矩阵。

对应的分配关系示意图如下。

比如cost矩阵如上，那么采用穷举法可以得到不同的分配cost 总和为

由此可以知，最小代价函数的分配方法为代价和5，对应的col_ind = [1,0,2]

3. KF对应的算法细节可参考卡尔曼滤波器的直观理解,此处不再赘述。

# -*- coding: utf-8 -*-
from __future__ import print_function

from numba import jit      # python的一个JIT库,通过装饰器来实现运行时加速
import os
import numpy as np
import matplotlib
#matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from skimage import io

import glob
import time
import argparse
from filterpy.kalman import KalmanFilter

np.random.seed(0)  #设置随机数种子


"""
Created on Thu Jan 19 12:40:07 2023

@author: scott
"""

"""
    SORT: A Simple, Online and Realtime Tracker
    Copyright (C) 2016-2020 Alex Bewley [email protected]

    This program is free software: you can redistribute it and/or modify
    it under the terms of the GNU General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version.

    This program is distributed in the hope that it will be useful,
    but WITHOUT ANY WARRANTY; without even the implied warranty of
    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.See the
    GNU General Public License for more details.

    You should have received a copy of the GNU General Public License
    along with this program.  If not, see .
    
"""


def linear_assignment(cost_matrix):
  try:
    import lap
    _, x, y = lap.lapjv(cost_matrix, extend_cost=True)
    return np.array([[y[i],i] for i in x if i >= 0]) #
  except ImportError:
    from scipy.optimize import linear_sum_assignment
    x, y = linear_sum_assignment(cost_matrix)
    return np.array(list(zip(x, y)))

# @jit
def iou(bb_test, bb_gt):
  """
  From SORT: Computes IOU between two bboxes in the form [x1,y1,x2,y2]
  """

  # bb_test 与bb_gt 都是二维, 将 ... 改为 :
  xx1 = np.maximum(bb_test[0], bb_gt[0])
  yy1 = np.maximum(bb_test[1], bb_gt[1])
  xx2 = np.minimum(bb_test[2], bb_gt[2])
  yy2 = np.minimum(bb_test[3], bb_gt[3])
  w = np.maximum(0., xx2 - xx1)
  h = np.maximum(0., yy2 - yy1)
  wh = w * h
  
  # IOU=（bb_test和bb_gt框相交部分面积）/(bb_test框面积+bb_gt框面积 - 两者相交面积[也就是两者的并集])
  # 详见 https://blog.csdn.net/scott198510/article/details/128697030 IoU loss
  o = wh / ((bb_test[2] - bb_test[0]) * (bb_test[3] - bb_test[1])                                      
    + (bb_gt[2] - bb_gt[0]) * (bb_gt[3] - bb_gt[1]) - wh)                                              
  return (o)  


def convert_bbox_to_z(bbox): 
  """
  将bbox由[x1,y1,x2,y2]形式转为 [边界框中心点x,框中心点y,框面积s,宽高比r], get a 4x1 array
  """
  w = bbox[2] - bbox[0]
  h = bbox[3] - bbox[1]
  x = bbox[0] + w/2.
  y = bbox[1] + h/2.
  s = w * h    # scale is just area
  r = w / float(h)
  return np.array([x, y, s, r]).reshape((4, 1))

##将[x,y,s,r]形式的bbox,转为[x1,y1,x2,y2], 与上面函数作用刚好相反
def convert_x_to_bbox(x,score=None):
  """
  Takes a bounding box in the centre form [x,y,s,r] and returns it in the form
    [x1,y1,x2,y2] where x1,y1 is the top left and x2,y2 is the bottom right
  """
  w = np.sqrt(x[2] * x[3])
  h = x[2] / w
  if(score==None):
    return np.array([x[0]-w/2.,x[1]-h/2.,x[0]+w/2.,x[1]+h/2.]).reshape((1,4)) # no score 1x4
  else:
    return np.array([x[0]-w/2.,x[1]-h/2.,x[0]+w/2.,x[1]+h/2.,score]).reshape((1,5)) # with score 1x5


class KalmanBoxTracker(object):
  """
  This class represents the internal state of individual tracked objects observed as bbox.
  """
  count = 0
  def __init__(self,bbox):
    """
    Initialises a tracker using initial bounding box.
    """
    #define constant velocity model
    self.kf = KalmanFilter(dim_x=7, dim_z=4) 
    self.kf.F = np.array([[1,0,0,0,1,0,0],[0,1,0,0,0,1,0],
                          [0,0,1,0,0,0,1],[0,0,0,1,0,0,0],
                          [0,0,0,0,1,0,0],[0,0,0,0,0,1,0],
                          [0,0,0,0,0,0,1]])
    self.kf.H = np.array([[1,0,0,0,0,0,0],[0,1,0,0,0,0,0],
                          [0,0,1,0,0,0,0],[0,0,0,1,0,0,0]])

    self.kf.R[2:,2:] *= 10.
    self.kf.P[4:,4:] *= 1000. #give high uncertainty to the unobservable initial velocities
    self.kf.P *= 10.
    self.kf.Q[-1,-1] *= 0.01
    self.kf.Q[4:,4:] *= 0.01

    self.kf.x[:4] = convert_bbox_to_z(bbox)
    self.time_since_update = 0
    self.id = KalmanBoxTracker.count
    KalmanBoxTracker.count += 1
    self.history = []
    self.hits = 0
    self.hit_streak = 0
    self.age = 0

  def update(self,bbox):
    """
    Updates the state vector with observed bbox.
    """
    self.time_since_update = 0
    self.history = []
    self.hits += 1
    self.hit_streak += 1
    self.kf.update(convert_bbox_to_z(bbox))

  def predict(self):
    """
    Advances the state vector and returns the predicted bounding box estimate.
    """
    if((self.kf.x[6]+self.kf.x[2])<=0):
      self.kf.x[6] *= 0.0
      
    self.kf.predict()
    self.age += 1
    
    if(self.time_since_update>0):
      self.hit_streak = 0
      
    self.time_since_update += 1
    self.history.append(convert_x_to_bbox(self.kf.x))
    return self.history[-1]

  def get_state(self):
    """
    Returns the current bounding box estimate.
    """
    return convert_x_to_bbox(self.kf.x)

# 将检测到的目标BBox与KF预测的BBox进行匹配
def associate_detections_to_trackers(detections,trackers,iou_threshold = 0.3):
  """
  Assigns detections to tracked object (both represented as bounding boxes)

  Returns 3 lists of matches, unmatched_detections and unmatched_trackers
  """
  if(len(trackers)==0): #如果跟踪器数量为空
    return np.empty((0,2),dtype=int), np.arange(len(detections)), np.empty((0,5),dtype=int)
  
  iou_matrix = np.zeros((len(detections),len(trackers)),dtype=np.float32) # 预分配检测器与跟踪器IOU矩阵
 
  for d,det in enumerate(detections): # 遍历目标检测器,每个BBox标记为d
    for t,trk in enumerate(trackers): # 遍历KF预测结果,每个BBox标记为t
      iou_matrix[d,t] = iou(det,trk)  # 计算检测器与预测跟踪的IOU并赋值给IOU矩阵对应位置 (i,j) -> (d—th detection, t-th tracker)
      
 
  #  加上负号是因为linear_assignment求的是最小代价组合, 而我们需要的是IOU最大的组合方式, 所以取负号
  
  # linear_assignment:通过匈牙利匹配算法将预测的BBox与检测的BBox匹配后以[d,t]坐标保存到matched_indices
  # 对于本文中的二维数据问题,得到matched_indices 是一个 n x 2 矩阵, 每一行第一列对应 d , 第二列对应 t
  matched_indices = linear_assignment(-iou_matrix)   # get index matrix 

  # 采用预分配全0矩阵后,默认的未分配匹配值的位置就为0
  # if min(iou_matrix.shape) > 0:
  #   a = (iou_matrix > iou_threshold).astype(np.int32) # 大于阈值坐标位置置为1,否则0
  #   if a.sum(1).max() == 1 and a.sum(0).max() == 1:
  #       matched_indices = np.stack(np.where(a), axis=1)
  #   else:
  #     matched_indices = linear_assignment(-iou_matrix)
  # else:
  #   matched_indices = np.empty(shape=(0,2))

  # 未匹配上的检测BBox 存入unmatched_detections 列表,表示有新的目标物进入了新一帧画面内, 后面要新增跟踪BBoxx ID
  unmatched_detections = []
  for d, det in enumerate(detections):
    if(d not in matched_indices[:,0]): # 每一行第一列就是 d: detection ID 
      unmatched_detections.append(d)

  # 未匹配上的预测BBox 存入 unmatched_trackers 列表, 表示前一帧的目标物在新一帧画面离开了, 后面要删除跟踪器BBox ID
  unmatched_trackers = []
  for t, trk in enumerate(trackers):
    if(t not in matched_indices[:,1]): # 每一行第二列对应 t: tracker ID
      unmatched_trackers.append(t)

  #filter out matched with low IOU, 过滤掉那些IOU较小的匹配对
  matches = [] # 存放过滤后的匹配结果
  for m in matched_indices: # m[0], m[1]  对应的是行列坐标 [d,t ]
    if(iou_matrix[m[0], m[1]]= self.min_hits or self.frame_count <= self.min_hits): # 画面中新跟踪器KF
          ret.append(np.concatenate((d,[trk.id+1])).reshape(1,-1)) # +1 as MOT benchmark requires positive
        i -= 1 # 实际的跟踪器id从 num-1 开始, i记录的是当前 trk 在self.trackers 中的KF从前往后添加进去的索引index [0, length-1]
        # remove dead tracklet, 超过生命周期的trk需要移除
        if(trk.time_since_update > self.max_age):
          self.trackers.pop(i) # 有效跟踪器中移除当前超过生命周期的KF
          
    if(len(ret)>0):
      return np.concatenate(ret)
    return np.empty((0,5))

def parse_args(): # 配置arg参数
    """Parse input arguments."""
    parser = argparse.ArgumentParser(description='SORT demo')
    
    #当你不add --display 的时候,默认为 False；add --display 的时候,才会触发 True 值。【符合常理】,store_false 反之亦然
    parser.add_argument('--display', dest='display', help='Display online tracker output (slow) [False]',action='store_true')
    
    parser.add_argument("--seq_path", help="Path to detections.", type=str, default='data')
    parser.add_argument("--phase", help="Subdirectory in seq_path.", type=str, default='train')
    parser.add_argument("--max_age", 
                        help="Maximum number of frames to keep alive a track without associated detections.", 
                        type=int, default=1)
    parser.add_argument("--min_hits", 
                        help="Minimum number of associated detections before track is initialised.", 
                        type=int, default=3)
    parser.add_argument("--iou_threshold", help="Minimum IOU for match.", type=float, default=0.3)
    # args = parser.parse_args(["--display"]) # display is True
    args = parser.parse_args() # # display is False by default
    return args

if __name__ == '__main__':
  # all train,  MOTchallenge 数据集
  sequences = ['PETS09-S2L1','TUD-Campus','TUD-Stadtmitte','ETH-Bahnhof','ETH-Sunnyday', \
               'ETH-Pedcross2','KITTI-17','ADL-Rundle-6','ADL-Rundle-8','Venice-2'] #路径list

  args = parse_args()       # args
  display = args.display    # 是否显示在屏幕上
  
  seq_path = args.seq_path  # 检测数据路径 ../data
  phase    = args.phase     # 子路径 ../data/train
  max_age  = args.max_age   # ID 生命周期 1
  min_hits = args.min_hits  # 最少关联的检测次数 3
  iou_threshold = args.iou_threshold # iou阈值 0.3
  
  total_time = 0.0  # 总时间初始化
  total_frames = 0  # 总帧数设置
  colours = np.random.rand(32, 3) # BBox显示的颜色设置
  if(display): # 如果要显示结果在屏幕上, 绘图初始化
    if not os.path.exists('mot_benchmark'):
      print('\n\tERROR: mot_benchmark link not found!\n\n    Create a symbolic link to the MOT benchmark\n    (https://motchallenge.net/data/2D_MOT_2015/#download). E.g.:\n\n    $ ln -s /path/to/MOT2015_challenge/2DMOT2015 mot_benchmark\n\n')
      exit()
    plt.ion()
    fig = plt.figure()
    ax1 = fig.add_subplot(111, aspect='equal')

  if not os.path.exists('../output'): # 设置或生成输出路径
    os.makedirs('./output')
  # pattern = os.path.join(seq_path, phase, '*', 'det', 'det.txt') # ../data/train/*/det/det.txt
  # det.txt: 帧数,-1, x, y, w, h, score, -1,-1,-1
  # sequences = glob.glob(pattern)
  for seq in sequences: # 循环遍历多个不同检测参数数据集
    mot_tracker = Sort(max_age, min_hits, iou_threshold) #生成一个 SORT tracker 实例
    pattern = './data/train/%s/det/det.txt'
    seq_dets_fn = pattern%(seq)
    seq_dets = np.loadtxt(seq_dets_fn, delimiter=',') # 加载检测参数
    # os.path.join('./output', '%s.txt'%(seq)
    output_path = './output/%s.txt'%(seq)
    with open(output_path,'w') as out_file:
      print("Processing %s."%(seq))
      for frame in range(int(seq_dets[:,0].max())): # 循环遍历各数据集, 确定视频序列总帧数
        frame += 1 # 检测视频序列帧数是从1开始
        dets = seq_dets[seq_dets[:, 0]==frame, 2:7] # #提取当前帧检测结果中的所有BBox参数[x1, y1, w, h, score]到dets
        dets[:, 2:4] += dets[:, 0:2] #转换 [x1,y1,w,h] to [x1,y1,x2,y2]
        total_frames += 1 # 总帧数+1

        if(display):
          fn = os.path.join('mot_benchmark', phase, seq, 'img1', '%06d.jpg'%(frame))
          im =io.imread(fn)
          ax1.imshow(im)
          plt.title(seq + ' Tracked Targets')

        start_time = time.time() # 当前系统时间
        
        # 将当前帧中目标检测器检测到的所有BBox送入SOTR实例,获得对所有物体的跟踪计算结果BBox
        trackers = mot_tracker.update(dets) # sort跟踪器计算更新
        
        cycle_time = time.time() - start_time #sort跟踪器耗时计算
        total_time += cycle_time #单个跟踪器耗时累加

        for d in trackers:
          print('%d,%d,%.2f,%.2f,%.2f,%.2f,1,-1,-1,-1'%(frame,d[4],d[0],d[1],d[2]-d[0],d[3]-d[1]),file=out_file)
          if(display):  #如果显示,将目标检测框画出来
            d = d.astype(np.int32)
            ax1.add_patch(patches.Rectangle((d[0],d[1]),d[2]-d[0],d[3]-d[1],fill=False,lw=3,ec=colours[d[4]%32,:]))

        if(display):
          fig.canvas.flush_events()
          plt.draw()
          ax1.cla()

  print("Total Tracking took: %.3f seconds for %d frames or %.1f FPS" % (total_time, total_frames, total_frames / total_time))

  if(display):
    print("Note: to get real runtime results run without the option: --display")