python计算机视觉 第四章照相机模型与增强现实
文章目录
- 引言
- 4.1针孔照相机模型
-
- 4.1.1照相机矩阵
- 4.1.2三维点的投影
- 4.1.3照相机矩阵分解
- 4.1.4计算照相机中心
- 4.2照相机标定
-
- 4.2.1一个简单地标定方法
- 4.3以平面和标记物体进行姿态评估
- 4.4增强现实
-
- 4.4.1PyGame和PyOpenGL
- 4.4.2从照相机矩阵到OpenGL格式
- 4.4.3在图像中放置虚拟物体
引言
本章中,我们将尝试对照相机进行建模,并有效地使用这些模型。在之前的章节里,
我们已经讲述了图像到图像之间的映射和变换。为了处理三维图像和平面图像之间
的映射,我们需要在映射中加入部分照相机产生图像过程的投影特性。
4.1针孔照相机模型
针孔照相机模型(有时称为射影照相机模型)是计算机视觉中广泛使用的照相机模
型。对于大多数应用来说,针孔照相机模型简单,并且具有足够的精确度。这个名
字来源于一种类似暗箱机的照相机。该照相机从一个小孔采集射到暗箱内部的光线。
在针孔照相机模型中,在光线投影到图像平面之前,从唯一一个点经过,也就是
照相机中心 C。

由图像坐标轴和三维坐标系中的 x 轴和 y 轴对齐平行的假设,我们可以得出针孔照
相机的投影性质。
照相机的光学坐标轴和 z 轴一致,该投影几何可以简化成相似三
角形。在投影之前通过旋转和平移变换,对该坐标系加入三维点,会出现完整的投
影变换。
在针孔照相机中,三维点 X 投影为图像点 x(两个点都是用齐次坐标表示的),如下
所示:
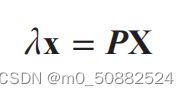
这里,3×4 的矩阵 P 为照相机矩阵(或投影矩阵)。
4.1.1照相机矩阵
照相机矩阵可以分解为:
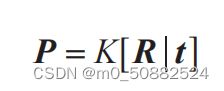
其中,R 是描述照相机方向的旋转矩阵,t 是描述照相机中心位置的三维平移向量,
内标定矩阵 K 描述照相机的投影性质。
标定矩阵仅和照相机自身的情况相关,通常情况下可以写成:
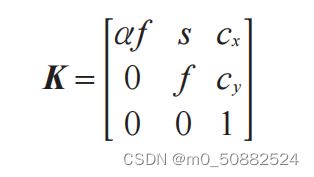
图像平面和照相机中心间的距离为焦距 f。当像素数组在传感器上偏斜的时候,需要
用到倾斜参数 s。在大多数情况下,s 可以设置成 0。
经过一系列的假设,我们就可以得到标定矩阵为

除焦距之外,标定矩阵中剩余的唯一参数为光心(有时称主点)的坐标 c=[cx,cy],
也就是光线坐标轴和图像平面的交点。因为光心通常在图像的中心,并且图像的坐
标是从左上角开始计算的,所以光心的坐标常接近于图像宽度和高度的一半。
4.1.2三维点的投影
下面来创建照相机类,用来处理我们对照相机和投影建模所需要的全部操作:
from scipy import linalg
from pylab import *
class Camera(object):
"""表示针孔照相机的类"""
def __init__(self, P):
"""初始化 P = K[R|t] 照相机模型"""
self.P = P
self.K = None # 标定矩阵
self.R = None # 旋转
self.t = None # 平移
self.c = None # 照相机中心
def project(self, X):
"""X(4×n的数组)的投影点,并进行坐标归一化"""
x = dot(self.P, X)
for i in range(3):
x[i] /= x[2]
return x
def rotation_matrix(a):
"""创建一个用于围绕向量a轴旋转的三维旋转矩阵"""
R = eye(4)
R[:3,:3] = linalg.expm([0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0])
return R
通过查询教材所提供的牛津数据图,并没有获得资源来进行下载,网上也没有搜寻到有关的资源,所以暂且没有进行此程序。
4.1.3照相机矩阵分解
如果给定如方程(4.2)所示的照相机矩阵 P,我们需要恢复内参数 K 以及照相机的
位置 t 和姿势 R。矩阵分块操作称为因子分解。这里,我们将使用一种矩阵因子分
解的方法,称为 RQ 因子分解。
将下面的方法添加到 Camera 类中:
def factor(self):
"""将照相机矩阵分解为 K,R,t,其中, R=K[R|t]"""
# 分解前3×3的部分
K,R = linalg.rq(self.P[:,:3])
# 将K的对角线元素设为正值
T = diag(sign(diag(K)))
if linalg.det(T) < 0:
T[1,1] *= -1
self.K = dot(K,T)
self.R = dot(T,R) # T的逆矩阵为其自身
self.t = dot(linalg.inv(self.K), self.P[:,3])
return self.K, self.R, self.t
RQ因子分解的结果并不是唯一的。在该因子分解中,分解的结果存在符号二义性。由于我们需要限制旋转矩阵R为正定的(否则,旋转坐标轴即可),所以如果需要,我们可以在求解到的结果中加入变换T来改变符号。
在示例照相机上运行下面的代码,观察照相机矩阵分解的效果:
import camera
K = array([[1000,0,500],[0,1000,300],[0,0,1]])
tmp = camera.rotation_matrix([0,0,1])[:3,:3]
Rt = hstack((tmp,array([[50],[40],[30]])))
cam = camera.Camera(dot(K,Rt))
print K,Rt
print cam.factor()
结果显示出现了很多AttributeError,现在目前还没有找到解决的方法,可以在网上进行搜寻。
4.1.4计算照相机中心
给定照相机投影矩阵 P,我们可以计算出空间上照相机的所在位置。照相机的中心
C,是一个三维点,满足约束 PC=0。对于投影矩阵为 P=K[R|t] 的照相机
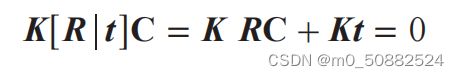
照相机的中心可以由下述式子来计算:

下面的代码可以按照上面公式计算照相机的中心。将其添加到 Camera 类中,该方法
会返回照相机的中心:
def center(self):
"""计算并返回照相机的中心"""
if self.c is not None:
return self.c
else:
# 通过因子分解计算c
self.factor()
self.c = -dot(self.R.T, self.t)
return self.c
4.2照相机标定
标定照相机是指计算出该照相机的内参数。在我们的例子中,是指计算矩阵 K。如
果你的应用要求高精度,那么可以扩展该照相机模型 , 使其包含径向畸变和其他
条件。对于大多数应用来说,公式中的简单照相机模型已经足够。
标定照相机的标准方法是,拍摄多幅平面棋盘模式的图像,然后进行处理计算。
4.2.1一个简单地标定方法
这里我们将要介绍一个简单的照相机标定方法。大多数参数可以使用基本的假设来
设定(正方形垂直的像素,光心位于图像中心),比较难处理的是获得正确的焦距。
对于这种标定方法,你需要准备一个平面矩形的标定物体(一个书本即可)、用于测
量的卷尺和直尺,以及一个平面。下面是具体操作步骤:
• 测量你选定矩形标定物体的边长 dX 和 dY; • 将照相机和标定物体放置在平面上,使得照相机的背面和标定物体平行,同时物
体位于照相机图像视图的中心,你可能需要调整照相机或者物体来获得良好的对
齐效果;
• 测量标定物体到照相机的距离 dZ; • 拍摄一副图像来检验该设置是否正确,即标定物体的边要和图像的行和列对齐;
• 使用像素数来测量标定物体图像的宽度和高度 dx 和 dy。
使用下面的相似三角形关系可以获得焦距:
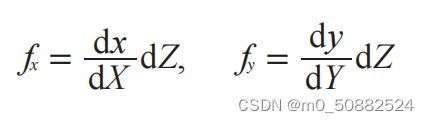
4.3以平面和标记物体进行姿态评估
4.4增强现实
增强现实(Augmented Reality,AR)是将物体和相应信息放置在图像数据上的一
系列操作的总称。最经典的例子是放置一个三维计算机图形学模型,使其看起来属
于该场景;如果在视频中,该模型会随着照相机的运动很自然地移动。如上一节所
示,给定一幅带有标记平面的图像,我们能够计算出照相机的位置和姿态,使用这
些信息来放置计算机图形学模型,能够正确表示它们。在本章的最后一节,我们将
介绍如何建立一个简单的增强现实例子。其中,我们会用到两个工具包:PyGame
和 PyOpenGL。
4.4.1PyGame和PyOpenGL
PyGame 是非常流行的游戏开发工具包,它可以非常简单地处理显示窗口、输入设
备、事件,以及其他内容。PyGame 是开源的,可以从 http://www.pygame.org/ 下
载。事实上,它是一个 Python 绑定的 SDL 游戏引擎。
PyOpenGL 是 OpenGL 图形编程的 Python 绑定接口。OpenGL 可以安装在几乎所
有的系统上,并且具有很好的图形性能。OpenGL 具有跨平台性,能够在不同的操
作系统之间工作。
我们使用OpenGL将一个三维模型放置在一个场景中。为了使用PyGame和PyOpenGL工具包来完成该应用,需要在脚本的开始部分载入下面的命令:
from OpenGL.GL import *
from OpenGL.GLU import *
import pygame,pygame.image
from pygame.locals import *
4.4.2从照相机矩阵到OpenGL格式
OpenGL 使用4×4 的矩阵来表示变换(包括三维变换和投影)。这和我们使用 的 3×4 照相机矩阵略有差别。但是,照相机与场景的变换分成了两个矩阵,GL_PROJECTION 矩阵和GL_MODELVIEW 矩阵GL_PROJECTION 矩阵处理图像成像的性质,等价于我们的内标定矩阵 K。GL_MODELVIEW 矩阵处理物体和照 相机之间的三维变换关系,对应于我们照相机矩阵中的R 和 t 部分。一个不同之处是,假设照相机为坐标系的中心,GL_MODELVIEW 矩阵实际上包含了将物体放置 在照相机前面的变换。
假设我们已经获得了标定好的照相机,即已知标定矩阵 K,下面的函数可以将照相机参数转换为 OpenGL 中的投影矩阵:
def set_projection_from_camera(K):
"""从照相机标定矩阵中获得视图"""
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
fx = K[0,0]
fy = K[1,1]
fovy = 2 * arctan(0.5*height / fy) * 180 / pi
aspect = (width*fy) / (height * fx)
# 定义近的和圆的裁剪平面
near = 0.1
far = 100.0
gluPerspective(fovy, aspect, near, far)
glViewport(0, 0, width, height)
模拟视图矩阵能够表示相对的旋转和平移,该变换将该物体放置在照相机前。模拟视图矩阵是个典型的4 x 4矩阵:
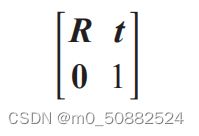
实现如何获得一处标定矩阵后的3X4针孔照相机矩阵,并创建一个模拟视图:
def set_modelview_from_camera(Rt):
"从照相机姿态中获得模拟视图矩阵"
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
#围绕x轴将茶壶旋转90度,使z轴向上
Rx = np.array([[1,0,0],[0,0,-1],[0,1,0]])
#获得旋转的最佳逼近
R = Rt[:,:3]
U,S,V = np.linalg.svd(R)
R = np.dot(U,V)
R[0,:] = -R[0,:]#改变x轴的符号
#获得平移量
t = Rt[:,3]
#获得4X4de模拟视图矩阵
M = np.eye(4)
M[:3,:3] = np.dot(R,Rx)
M[:3,3] = t
#转置并压平以获取列序数值
M = M.T
m = M.flatten()
#将模拟视图矩阵替换为新的矩阵
glLoadMatrixf(m)
4.4.3在图像中放置虚拟物体
我们需要做的第一件事是将图像(打算放置虚拟物体的图像)作为背景添加进来。
在 OpenGL 中,该操作可以通过创建一个四边形的方式来完成,该四边形为整个视
图。完成该操作最简单的方式是绘制出四边形,同时将投影和模拟试图矩阵重置,
使得每一维的坐标范围在 -1 到 1 之间。
def draw_background(imname):
""" 使用四边形绘制背景图像 """
# 载入背景图像(应该是 .bmp 格式),转换为 OpenGL 纹理
bg_image = pygame.image.load(imname).convert()
bg_data = pygame.image.tostring(bg_image,"RGBX",1)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
# 绑定纹理
glEnable(GL_TEXTURE_2D)
glBindTexture(GL_TEXTURE_2D,glGenTextures(1))
glTexImage2D(GL_TEXTURE_2D,0,GL_RGBA,width,height,0,GL_RGBA,GL_UNSIGNED_BYTE,bg_data)
glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MAG_fiLTER,GL_NEAREST)
glTexParameterf(GL_TEXTURE_2D,GL_TEXTURE_MIN_fiLTER,GL_NEAREST)
# 创建四方形填充整个窗口
glBegin(GL_QUADS)
glTexCoord2f(0.0,0.0); glVertex3f(-1.0,-1.0,-1.0)
glTexCoord2f(1.0,0.0); glVertex3f( 1.0,-1.0,-1.0)
glTexCoord2f(1.0,1.0); glVertex3f( 1.0, 1.0,-1.0)
glTexCoord2f(0.0,1.0); glVertex3f(-1.0, 1.0,-1.0)
glEnd()
# 清除纹理
glDeleteTextures(1)