车流量统计(2)
车流量统计(2)
- 目标估计模型-卡尔曼滤波
- 匈牙利算法
- KM算法
- 数据关联
- SORT
目标估计模型-卡尔曼滤波
主要完成卡尔曼滤波器进行跟踪的相关内容实现:
初始化:卡尔曼滤波器的状态变量和观测输入
更新状态变量
根据状态变量预测目标的边界框。
1.初始化
状态量是一个七维向量:
得到了状态转移矩阵F
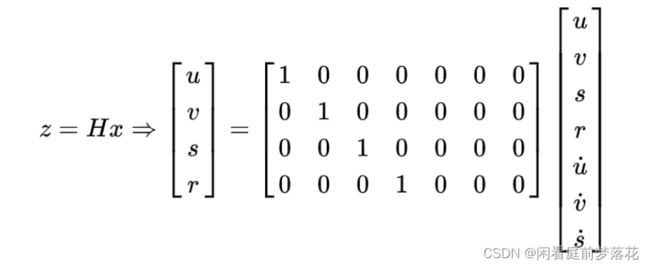
量测矩阵H是一个4*7矩阵将观测值和状态变量相对应
协方差参数根据经验值设定:

包含两个噪声测量噪声和激励噪声,两个协方差矩阵。
def __init__(self,box)
#定义等速模型
#7个状态变量和4个观测输入
self.kf=KalmanFilter(dim_x=7,dim_z=4)
self.kf.F = np.array([])#状态转移矩阵
#先验协方差P
self.kf.P[4:,4:]*=1000.
self.kf.P*=10.
self.kf.H=np.array([]) #对观测值预测所需要的协方差矩阵,测量矩阵
#测量噪声的协方差R,即真实值与测量值差的协方差
self.kf.R[2:,2:]*10 #单位矩阵两行两列之后全部乘以10
#是过程激励噪声的协方差Q
self.kf.Q[-1,-1]*=0.01
self.kf.Q[4:,4:]*=0.01
#状态估计
self.kf.x[:4] = convert_bbox_to_z(bbox)
#参数更新
self.time_since_update=0
self.id=KalmanBoxTracker.count
KalmanBoxTracker.count += 1
self.history = []
self.hits = 0
self.hit_streak = 0
self.age = 0
更新状态变量,使用观测到的目标框更新状态变量
def update(self,bbox):
#重置
self.time_since_updata=0
self.history=[]
#hits计数加1
self.hits+=1
self.hit_streak+=1
self.kf.update.(convert_bbox_to_z(bbox))
进行目标框的预测
推进状态变量并返回预测的边框结果
def predict(self):
#推进状态变量
if (self.kf.x[6]+self.kf.x[2])<=0:
self.kf.x[6]*=0.0
#进行预测
self.kf.predict()
#卡尔曼滤波次数
self.age+=1
#若过程中未更新将hit_streak置为0
if self.time_since_update>0:
self.hit_streak=0
self.time_since_update+=1
self.history.append(convert_x_to_bbox(self.kf.x))
return self.history[-1]
匈牙利算法
匈牙利算法与KM算法是用来解决多目标跟踪中的数据关联问题,匈牙利算法与KM算法都是为了求解二分图的最大匹配问题。
匈牙利算法是一种在多项式时间内求解分配任务分配的组合优化算法。
匈牙利算法api
from scipy.optimize import linear_sum_assignment
import numpy as np
cost =np.array([[1,2,3,4],[2,4,6,8],[3,6,9,12],[4,8,12,16]])
row_ind,col_ind=linear_sum_assignment(cost)
print("行索引:\n{}".format(row_ind))
print("列索引:\n{}".format(col_ind))
print("匹配度:\n{}".format(cost[row_ind,col_ind]))
按照这个分配不是我们心中的最优的,匈牙利算法将每个分配对象视为同等地位,在前提下求解最大匹配问题。
KM算法
解决的是带权二分图的最优匹配问题
第一步:首先对每个顶点赋值,称为顶标,将左边的顶点赋值为与其相连的边的最大权重,右边的顶点赋值为0.
第二步:匹配的原则是只和权重与左边分数相同的边进行匹配,若找不到匹配,则对此条路径的所有左边顶点的顶标减d,所有右边的顶标加d。
一种替代KM算法的思想是:用匈牙利算法找到所有的最大匹配,比较每个最大匹配的权重,再选出最大权重的最优匹配即可得到更贴近真实情况的匹配结果。但这种方法时间复杂度较高,会随着目标数越来越多,消耗的时间大大增加,实际应用中并不推荐。
数据关联
利用匈牙利算法对目标框和检测框进行关联
在这里我们对检测框和跟踪框进行匹配,整个流程是遍历检测框和跟踪框,并进行匹配,匹配成功则保留,未成功则删除
def associate_detection_to_trackers(detection,trackers,iou_threshold=0.3):
将检测框越卡尔曼滤波器的跟踪框进行关联匹配
if (len(trackers) == 0) or (len(detections) == 0):
return np.empty((0, 2), dtype=int), np.arange(len(detections)), np.empty((0, 5), dtype=int)
#iou不支持数组计算,逐个计算两两之间的交并比,调用linear_assignment
iou_matrix=np.zeros(len(detection),len(trackers),dtype=np.float32)
#遍历目标检测框
for d,det in enumerate(detection):
#遍历跟踪框
for t,trk in enumerate(trackers):
iou_matrix[d,t]=iou(det,trk)
result=linear_sum_assignment(-iou_matrix)
matched_indices = np.array(list(zip(*result)))
#记录未匹配的检测框和跟踪框
#未匹配的检测框放入unmatched_detection中,表示有新目标进入画面,要新增跟踪器目标
unmatcher_trackers=[]
for t,trk in enumerate(trackers):
if t not in matched_indices[:,1]:
unmatched_trackers.append(t)
# 未匹配的跟踪框放入unmatched_trackers中,表示目标离开之前的画面,应删除对应的跟踪器
unmatched_trackers = []
for t, trk in enumerate(trackers):
if t not in matched_indices[:, 1]:
unmatched_trackers.append(t)
#将匹配成功的跟踪框放入matches中
matces=[]
for m in matched_indices:
if iou_matrix[m[0], m[1]] < iou_threshold:
unmatched_detections.append(m[0])
unmatched_trackers.append(m[1])
else:
matches.append(m.reshape(1, 2))
# 初始化matches,以np.array的形式返回
if len(matches) == 0:
matches = np.empty((0, 2), dtype=int)
else:
return matches, np.array(unmatched_detections), np.array(unmatched_trackers)
SORT
SORT核心是卡尔曼滤波和匈牙利匹配两个算法。整体拆分为两个部分,分别是匹配过程和卡尔曼预测加更新过程。
关键步骤:
轨迹卡尔曼滤波预测,使用匈牙利算法将预测后的track和当前帧的detection进行匹配(IOU匹配)、卡尔曼滤波更新。