读论文：A novel framework for spatio‑temporal prediction of environmental data using deep learning

标题: 利用深度学习对环境数据进行时空预测的新框架
作者: Federico Amato, Fabian Guignard, Sylvain Robert & Mikhail Kanevski

---

Abstract

虽然深度学习模型能够通过其自动特征表示学习来捕获时空依赖关系，但在空间中一组不规则点上测量的连续时空场的插值问题仍在研究中。为此，文本介绍了一种对气候和环境数据进行时空预测的框架。具体而言，就是展示了如何将时空过程分解为以时间为参照的基础函数和随机空间系数的乘积。并将其应用到模拟和真实世界的数据上，显示所提出的框架在模拟连贯的时空场方面的有效性。

Index Term——spatio‑temporal prediction, deep learning.

---

Introduction

研究人员发现可以讲ML运用到在气候建模和预测方面上。而捕捉环境时空数据空间、时间和时空相关性的特点可以通过DL来实现。但是，大部分的努力都集中在固定地点的连续或离散的时空场的测量。但由于这种数据来源于卫星或气候模型，容易因云层而造成数据丢失。

为了解决上述问题，本文提出了利用空间不规则分布的时间序列数据在规则网格上重建时空场的方法，以此来利用空间不规则分布的时间序列数据在规则网格上重建时空场。该方法允许模拟非平稳时空过程，还可用于插值气候和环境变量的地面测量，同时考虑到数据中存在的时空依赖性。

---

贡献

1. 提出了一种基于深度分布的气候和环境数据时空预测框架；
2. 有效的解决了随机系数的空间预测的问题；
3. 通过使用单个DL模型可以开发具有多个输出的网络结构，从而对它们进行一致的建模；

---

综述

一、相关工作

利用graph-CNNs研究了非欧几里得空间图的地理空间问题。生成对抗网络GAN也与局部自相关措施一起使用，以改善空间模式的表示。但是这种方法没有考虑所研究现象的时间维度。

关于预测问题，考虑不同测量位置之间相关性的常用方法是将它们视为图中的节点，然后可以使用特定的DL架构对其建模。但是这种方法只能在测量站的空间位置进行预测，而不能在任何潜在的空间位置进行预测。也正因如此，本文提出了新框架来应对这一问题。

---

二、方法

在处理时空现象时，很难真实地再现数据中的空间、时间和时空依赖关系。考虑这些依赖关系的一种方法是采用基函数表示。本文使用通过主成分分析(PCA)获得的降阶基，也称为气候学、气象学和海洋学领域的经验正交函数(EOFs)分解。

基本思想：分解在数理统计学的多变量分析中称为主分量分析。主分量分析是利用降维思想，在损失很少信息的前提下，把多个指标转化成几个综合指标的多元统计方法；

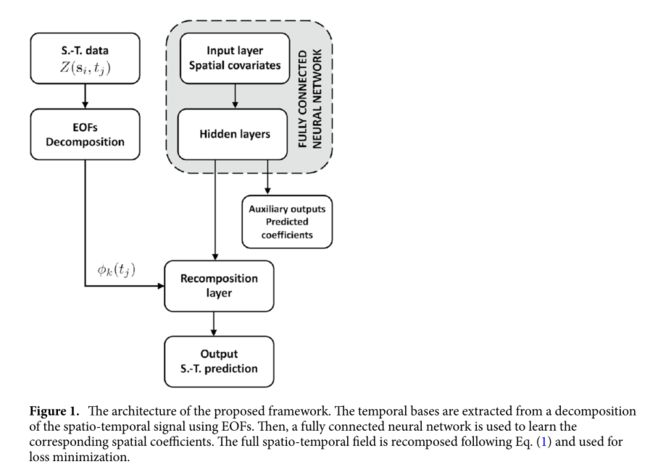
本文提出的从一组不规则空间点的测量开始对连续时空场进行插值的框架包括以下步骤。首先，使用基函数表示从时空观测中提取固定的时间基;然后，使用DL回归技术在任何所需的空间位置对对应于每个基函数的随机空间系数进行联合建模。最后，重构时空信号，返回场的时空插值。

---

2.1 利用EOFs进行时空数据分解

假设我们在S个空间位置{s_i: 1≤i≤S}和T个时间指数{t_j: 1≤j≤T}上有时空观测{Z(s_i, t_j)}。设^~ Z(s_i, t_j)为空间中心数据：

其中，
这个是tj时刻的整体均值

中心数据^~ Z(s_i, t_j)可以用离散的时间标准正交基表示{Φk(tj)}^K_k=1，即：

其中，

其中α_k(s_i)为空间位置s_i处第K个基函数Φ_k的系数，K = min{T, S−1}。注意标量系数α_k(s_i)只取决于位置而不取决于时间，而时间基函数Φ_k(t_j)与空间无关。第一个分解在理论上由Karhunen-Loève expansion31证明，它是基于Mercer的定理；

---

2.2 系数建模

潜在截断EOFs分解返回每个空间位置s_i，对应于原始观测值^~ K随机系数α_k(s_i)。这些系数可以在空间上建模，并映射到规则网格上，解决插值/回归任务。

为了证明所提出方法的有效性，本文使用深度前馈全连接神经网络(对系数建模。

全连接神经网络（Fully connected neural network,FCNN）：从第二层神经元开始，每一层的每个神经元都与前一层的所有神经元相连接；从第一层开始，除最后一层，每一层神经元都有后一层所有神经元之间相连接，并且层内神经元互不相连

网络结构如下图所示：

空间协变量被用作具有第一辅助输出层的神经网络的输入，其中空间系数被建模。然后，重组层将使用EOFs分解产生的^~ K建模系数和时间基Φ_k，以重建最终输出，即——时空场跟随式(1)

该网络有多个输入，即空间协变量(流经整个堆栈层)和直接连接到输出层的时间基。它也有多个输出，即每个基的空间系数，都是联合建模的，以及输出信号。

所提出的DL方法有两个主要优点：

• 首先，大多数经典的ML回归算法不能处理多个输出，因此必须为每个系数映射拟合单独的模型，而不能利用任务之间的相似性；
• 其次，本文提出的深度学习方法最小化了对最终预测目标(即重构感兴趣的时空场)的直接损失；

---

2.3 时空半变异函数

半变异函数可以用来描述数据集的时空相关结构。(各向同性)经验半变异函数如下所示：

其中N_s(h)是在一定公差范围内由欧几里得距离h分隔的所有位置对的集合，N_t(τ)是在一定公差范围内由τ的时间延迟分隔的所有时间点的集合，#表示集合的基数

在本研究中，通过残差分析

一种确定有关变量$\epsilon$(也就是函数中的常数项/偏差值)的假定是否成立的方法

利用变异学来了解模型从原始数据中提取的时空依赖关系的质量和数量。

---

三、实验结果

在模拟时空场，和真实的温度测量数据集上应用该框架。

空间系数图采用全连接前馈神经网络建模。其配置如下所示：

• 内核初始化器:He初始化;激活函数:ELU;
• 正规化:早期停止；
• 优化器:Adam;
• 学习率调度:1Cycle调度;
• 隐藏层数:6;
• 每层神经元:100个;
• 损失函数:平均绝对误差；

---

3.1 模拟数据集实验

为了产生真实的二维空间模式，从R库中模拟了20个具有高斯核的高斯随机场，并记作X_k(s)， k = 1，…20。长度为T = 1080的时间序列Y_k(t_j)，当k = 1，…， 20，使用一阶自回归模型生成。然后，将模拟的时空数据集作为空间随机场X_k(s)的线性组合，其中Y_k(t_j)作为时刻系数的作用，如下所示：

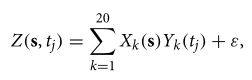
其中ε是由均值为零且标准差等于无噪声场标准差的10%的高斯分布产生的噪声项。空间点s_i, i = 1，…， S = 2000是在139 × 88的常规二维空间网格上均匀采样，构成训练位置。
通过对训练位置的场序列进行评估，生成时空训练集{Z(si, tj)}。时空验证集和测试集分别以类似的方式从随机选择的1000个位置生成

前50个分量的相对方差累积百分比如图2所示：

请注意，如果不添加ε项，总方差将用前20个分量解释，这是用于构建模拟数据集的元素数量；
即使存在额外的噪声，这些分量也可以解释约99%的方差。因此，神经网络使用两个输入进行训练，即对应于x和y坐标的空间协变量和^~K = 20输出

用所提出的神经网络方法建模后在测试集上计算的平均绝对误差(MAE)如表1所示：

没有使用所提出的多输出模型一次性预测所有空间系数，而是研究了由于每个系数图的单独建模在测试误差性能方面的影响。
本文采用全连接前馈神经网络(NN)和常用的随机森林(RF)方法对单个空间系数图进行预测，并将其与时间基结合起来重建时空场。
结果表明，使用所提出的多输出模型可以显著提高基于单独单输出模型的方法的性能，这些方法的性能明显较差

下图显示了随机选择的预测图和时间序列示例，并将其与真实时空场进行了比较。预测的地图恢复了真实的空间模式，时间行为也被很好地复制：

由Eq.(2)定义的模拟时空场的模型输出。左上:真实空间场在固定时间的快照，在下面的时间图中垂直虚线表示。右上:同时预测的地图。底部:真实的时间序列(黑色)和预测的时间序列(橙色)在上面的地图中标记为十字的固定位置。

下图显示了模拟数据、模型输出和残差的时空半变异函数，模拟数据与模型数据之间的差异：

在模拟数据的测试点上计算了时空半变异函数(左)，使用前20个EOFs分量实现的模型(中)及其残差(右)
模拟数据上的半变异函数显示了插值如何恢复了与(真实)模拟数据相同的时空结构，尽管其值略低。这意味着该模型已经能够解释这种现象的大部分时空变异性；
残差的半变异函数中几乎没有显示出结构，这表明几乎所有的空间和时间结构化信息——或者至少是由两点统计量如半变异函数描述的信息——已经从数据中提取出来；

---

3.2 温度监测网络实验

提出的框架在模拟现实世界气候和环境现象方面的有效性在欧洲一个复杂的高山地区的气温预测案例研究中得到了检验，这是一个具有挑战性但具有代表性的例子。

对训练集和验证集进行EOFs分解得到的前三个分量，以及相应的时间基函数和归一化空间系数如图5所示：

首先对EOFs的3个组成部分进行分解。第一行:时间上引用的基函数。中间行:对应EOFs的归一化空间系数。最下面一行:由全连接神经网络(所有组件)的辅助输出提供的相应预测空间系数；
前两个时间基础清楚地显示了年周期。归一化空间系数图在不同空间尺度上呈现出不同的格局。
图5底排的第一张地图清楚地显示了阿尔卑斯山链中第一个时空基础的贡献，而第三张地图显示了该链南部的相应时空基础的强烈负贡献

图6显示95%的数据变化是由前24个分量解释的：

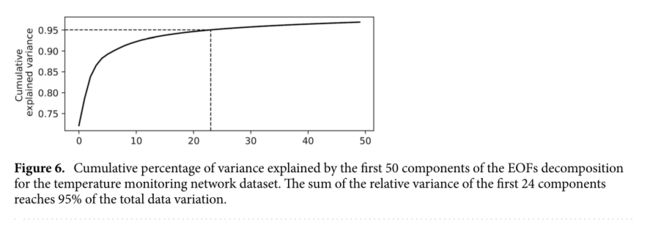
本文实现了两个不同的模型：

• 第一个是通过使用所有可用的成分(~ K = K = 294)来开发的；
• 第二个则采用压缩信号，保持95%的数据方差(~ K = 24)；

又由于温度与海拔也有密切关系，所以除了纬度和经度之外，还添加了海拔作为空间协变量，也就意味着有三个输入。

图7显示了两种模型在随机选择的固定时间的温度预测图，以及随机试验站的时间序列：

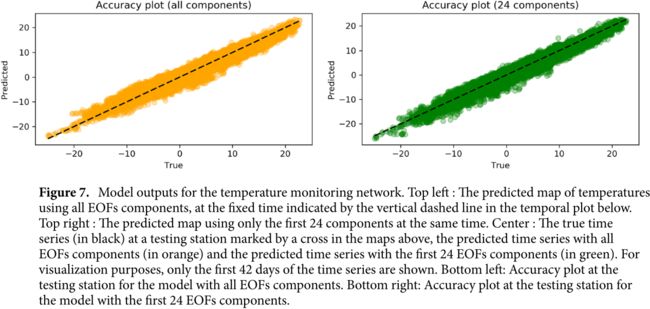
左上:使用所有EOFs成分的温度预测图，在下面的时间图中垂直虚线所示的固定时间；
右上:同时只使用前24个成分的预测地图；
中间:上图中由十字标记的试验站的真实时间序列(黑色)，包含所有EOFs成分的预测时间序列(橙色)和包含前24个EOFs成分的预测时间序列(绿色)。
为了可视化，只显示时间序列的前42天。左下:模型测试站的精度图，包含所有EOFs组件。右下:具有前24个EOFs组件的模型在试验站的精度图
在精度图和时间序列图上将试验站的预测温度与真实测量值进行比较。K = 294的模型极好地复制了温度行为。预测的地图捕捉了不同的气候带，而预测的时间序列很好地检索了数据中的时间依赖性；
准确度图进一步突出了预测与真实值的吻合程度。具有~ K = 24的模型显示了类似的结果，而数据的维数已显著降低，这表明有可能通过压缩数据获得类似的准确性；

---

3.3 结论

使用单独的回归模型对于具有所有组件的模型和具有前24个组件的模型都导致了更高的误差。在这两种情况下，使用单一输出策略导致RF和神经网络模型之间的错误率相当；

• 结论：使用单个网络来联合建模空间系数和时空场会产生更好的性能，因为该算法被训练为最小化信号重组后对最终输出计算的损失；
• 不足：在使用24个成分的模型数据上计算的半变量图的边沿略低，表明模型没有捕捉到数据的一定程度的变异性，这与训练数据中约5%的变异性没有被前24个分量所解释有关。还可以看出来，残差仍然显示出小的时间相关性。这表明，即使空间分量模型被正确建模，一些时间上的依赖性也可能存在；

---

总结

本文介绍了一种基于深度分布的气候和环境数据时空预测框架。

其优点有：

• 将时空信号分解为固定的时间基和随机空间系数，可以从空间不规则分布的测量数据开始完全重建时空场；
• 虽然随机系数的空间预测可以使用任何回归算法来执行，但由于其自动特征表示学习，DL算法特别适合解决这个问题；
• 本文所提出的框架还能够捕获数据中的非线性模式，因为它通过空间系数映射将时空场建模为时间基产品的组合；

---

未来展望

1. 还需要进一步的研究来确定程序，以量化不确定性在拟议框架的不同步骤中的传播；
2. 必须进行进一步的研究，以分析该框架提供的时空预测的一致性，以及更普遍的由任何其他数据驱动的方法与决定所研究现象的真实物理模型中观察到的模式的一致性；