智能车循迹避障磁铁检测比赛

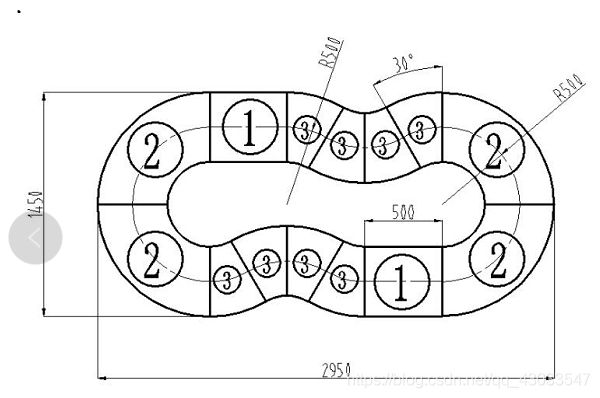
比赛要求

比赛时赛道元素不超出训练赛道包含的范围，形状和长度等会有变化。正式比赛时现场公布比赛赛道。
所有参赛队使用的车模参数如下：

传感器：电磁传感器、LED指示灯、编码器、超声波、干簧管，OLED显示屏等；
输出设备：舵机1个，直流电机2个；
支持图形化编程，支持标准USB、蓝牙下载通讯；
小车车模尺寸：31018075mm 各项偏差不大于±10%
小车车模重量：0.7Kg±10%

智能车放在发车区，发出时车头处于计时装置前方20-30cm处.

小初中赛道：

小初基本任务：

从发车到小车沿赛道跑完两圈，称为一个回合。
基本任务：发车，停止，循迹
小车放置在发车区内自动出发，沿着铜线的轨迹行走，小车完成一个回合运行后，在终点指定区域内停车。
附加任务：磁铁检测、鸣笛、亮灯
发车鸣笛，转弯时相应的灯亮，检测磁铁的位置

高中赛道

高中基本任务：

基本任务：超声波挡板发车，停止，循迹
小车放置在发车区内挡板前20~30cm，撤掉挡板后自动出发，沿着铜线的轨迹行走，小车完成一个回合运行后，在终点指定区域内停车。
附加任务：磁铁检测、避障、鸣笛、亮灯
发车鸣笛，转弯时相应的灯亮，小车自动避开赛道内或外侧放置障碍物，在遇到障碍物时进行鸣笛并且亮灯，检测磁铁的位置

任务分析

器材

1. 智能车

2. 舵机（控制前面两个轮胎转向）

3. 电机（控制后面两个轮胎前进后退）

4. 编码器（控制电机）

5. 电磁传感器（循迹）

6. LED指示灯

7. 蜂鸣器

8. 超声波传感器（撤销挡板启动）

9. 干簧管（检测磁铁）

10. OLED显示屏

分析

疑问

1. 按键发车——打开电源之后车辆上电，按发车键后车辆启动，这样是不是需要再装一个按键啊？
2. 磁铁的位置在哪，检测到磁铁后需要做什么样的动作？
3. 避障用超声波传感器检测

知识讲解

2. 转向问题，舵机输出角度是（225-30,225，225+30），舵机输出量=舵机增量+舵机中值，舵机增量限制在正负30以内
3. 两数之差除以两数之和得到的值叫做相对偏差
4. 电磁信号滤波，采集20次去掉最大值和最小值，取18次的平均值。
5. 左路电磁信号与右路电磁信号的差，当车偏离轨道时，差会变大，此时需要舵机快速动作，所以会增大舵机增量。
6. 111待编辑…

在这里插入代码片

电机

当通电之后，看电机是否正常转动，是否有抖动、反转。
通电后电机正常转动。写一个电机程序，看电机能否正常运行

舵机

把运行中的车拿起来，放到赛道的电磁线上方，把左电磁传感器慢慢靠近赛道电线，看车轮是否在往左转；把右电磁传感器慢慢靠近赛道电线，看车轮是否在往右转。如果是，说明电磁传感器和舵机是正常的。

电磁循迹的计算方法：
舵机输出量 = 舵机中值（225） + 舵机增量
舵机增量 = 左右电磁值差 × 放大比例系数 ÷左右电磁值和，这个是粗略的算法，下面会提出位置式PID算法来控制舵机打角。

舵机中值的调整

一开始要把舵机中间的螺丝拆下来，设定中值为225之后，运行舵机程序，在重新安装回去，在运行，若舵机此时在中间位置，说明该值为舵机中值。
舵机中值225
舵机输出量：
向左变大225+30
向右变小 225-30

调试电磁传感器

电磁信号检测：靠近的话会很大300~500
电磁差=左电磁-右电磁
左移——>右电磁大——负数
右移——>左电磁大——正数

小车测试：

对小车进行编号，测试小车们能否正常跑圈。主要测试原件的好坏

编号1 ——225
编号3 ——舵机中值 235，电机声音太大，舵机和电机有问题
编号4 ——舵机有问题 中值为245
编号5 ——235
编号7 ——舵机拧不动，电机更换

过弯道时，小车有5种状态，
a为左右电磁的差值，b为一个常数
1，电磁传感器左边的值会很大，右边的值小，电磁左值－电磁右值=a，会很大，a>b,并且a>0,舵机增量要大一点，让他左大拐弯。

2，电磁传感器左边大，右边小，a差不多大，0,舵机增量略微大，左小拐弯

3，电磁传感器两边的值一样大，但也有偏差，电磁左值－电磁右值=a，a应该在0的左右变动，a=0,舵机增量为0，直行

4，电磁传感器右边大，左边小，a差不多小，-b,舵机增量略微小，右小拐弯

5，电磁传感器右边的值会很大，右边的值小，电磁左值－电磁右值=a，会很大，a<-b,并且a<0,舵机增量更小，让他右大拐弯。

归一化

归一化就是将所有数据都变成0-1之间的数，将数据映射到0～1范围之内处理，使数据观察更便捷快速。在电磁车行驶过程中，由于需要通过分析各个电感采集值的情况来判定前方为何种路段，所以更要求这些采集值有迹可循，归一化便是一种很好的方法，先将所有采集到的值缩小到0-1范围内，再适当放大（常见的放大倍数为100），这样既能更容易的由电磁值分析出路况，又不会因为数据过小而失真。

归一化的公式如下：(x-Min)/（Max-Min）。
其中，x为实时检测到的变量，Min与Max为标定的电感采集最小与最大值。

滤波

滤波是将信号中特定波段频率滤除的操作，是抑制和防止干扰的一项重要措施。它可以从含有干扰的接收信号中提取有用信号，很大程度上保证了采集到的信号的真实性和稳定性。正因如此，滤波算法也成了在智能车控制中不可或缺的一种控制算法。

算术平均值滤波，指的是将每个电感采集到的一组值用冒泡排序按从大到小或者从小到大的顺序排布，再丢弃最大值与最小值，取剩下数据的算术平均数.

PD控制舵机

在介绍PID算法前，我们可以试想一下，如果没有某些特殊的算法，那么我们会如何**控制舵机打角和电机转速？**

就舵机而言，其结论可能是，设定一个特定的值，当左右电感的电磁值之差达到这个设定的值时，便控制舵机向左或向右打一定的角度（或者多设值，分不同情况多段打角），这种算法虽然能够让赛车在赛道上行驶，但打角不够顺滑，反应也不够灵敏，

这时我们便需要将这个差值代入某个算法，令其与舵机打角关联起来，这样便可以得到一个较为连贯与精确的舵机输出值，有利于赛车更完美的运行，而这种将差值与最后输出值关联起来的算法便是我们常说的PID控制算法。

PID控制是将误差信号e(t)的比例§，积分(I)和微分(D)通过线性组合构成控制量进行控制，是对误差信号进行处理，但是计算机控制是一种采样控制，不能使用连续系统的PID算法，他只能根据采样时刻的偏差来计算控制量，因此计算机控制系统中，必须对公式进行离散化，具体就是用求和代替积分，用向后差分来代替微分，使模拟PID离散化为数字形式的差分方程。

连续PID：

位置式PID：

增量式PID：

	比例P :    e(k)-e(k-1)   这次误差-上次误差
	
	积分I :   e(i)     误差   

	微分D :  e(k) - 2e(k-1)+e(k-2)   这次误差-2*上次误差+上上次误差

在位置式PID中，因为有误差积分 ∑e(i)的一直累加，也就是当前的输出u(k)与过去的所有状态都有关系，或许会用到误差的累加值；（误差e会有误差累加），输出的u(k)对应的是执行机构的实际位置，一旦控制输出出错(控制对象的当前的状态值出现问题 )，u(k)的大幅变化会引起系统的大幅变化。

并且位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积，一旦误差开始反向变化，系统需要一定时间从饱和区退出，所以在u(k)达到最大和最小时，要停止积分作用，并且要有积分限幅和输出限幅。

所以在使用位置式PID时，一般我们只使用PD控制
位置式PD控制思路

void steer_control()   //舵机控制函数
{
    error=AD_M_Left[0]-AD_M_Right[0];//当前误差=左电磁的值-右电磁的值
    
    direction_controlout=dirP*error+dirD*(error-lasterror);//舵机增量=P*误差+D*（当前误差-上一次误差），上一次误差初值为0
    angle=mid_angle+direction_controlout;//舵机输出量=舵机中值+舵机增量
    
    angle=angle>right_angle?right_angle:angle;//对舵机输出量进行限制
    angle=angle<left_angle?left_angle:angle;
    
    PWM_SetSteer((int)angle); //控制舵机打角
    lasterror=error;//把当前误差值传给lasterror
    
}

如下图所示：小车要右拐时， error=AD_M_Left[0]-AD_M_Right[0]<0，我们要用pid调节舵机增量，控制舵机输出，使舵机往右打角，通过负反馈，使得电磁左值增大，电磁右值减小，让error为0,。

调程序时，主要调PD参数的大小，比较难调啊！！！要是可以仿真就好了！

分段控制
在PD参数中，P参数控制响应速度，D参数消除稳差，那么可以想到，如果全局使用同一个PD参数，则会出现无法控制既在直道上平稳运行，又能很好的过各种弯道的局面。这时候就需要我们对PD参数进行分段控制。
而由于电磁车只能依靠电感传回的电磁信号判断赛道路况，所以可以将左右两边的电感值差作为分段控制的依据。

PID控制电机

在对电机的控制中，采用增量式PID算法，首先要设定一个目标速度，再将当前速度与其比较，得出的差值代入公式计算，从而控制电机转速。

增量式PID根据公式可以很好地看出，一旦确定了 KP、KI 、KD，只要使用前后三次测量值的偏差， 即可由公式求出控制增量

而得出的控制量Δu(k)对应的是近几次位置误差的增量，而不是对应与实际位置的偏差 没有误差累加

也就是说，增量式PID中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果，并且在系统发生问题时，增量式不会严重影响系统的工作。

增量型 PID，是对位置型 PID 取增量，这时控制器输出的是相邻两次采样时刻所计算的位置值
之差，得到的结果是增量，即在上一次的控制量的基础上需要增加（负值意味减少）控制量。

增量式PID控制思路：

typedef struct PID
{ 
  float P,I,D,limit;
}PID;
typedef struct Error
{
  float Current_Error;//当前误差
  float Last_Error;//上一次误差
  float Previous_Error;//上上次误差
}Error;
 
/*! 
 *  @brief      增量式PID
 *  @since      v1.0
 *  *sptr ：误差参数
 *  *pid:  PID参数
 *  NowPlace：实际值
 *  Point：   期望值
 */
// 增量式PID电机控制
int32 PID_Increase(Error *sptr, PID *pid, int32 NowPlace, int32 Point)
{
 
	int32 iError,	//当前误差
		Increase;	//最后得出的实际增量
 
	iError = Point - NowPlace;	// 计算当前误差
 
	Increase =  pid->P * (iError - sptr->Last_Error)   //比例P
			  + pid->I * iError      //积分I
			  + pid->D * (iError - 2 * sptr->Last_Error + sptr->Previous_Error);  //微分D
	
	sptr->Previous_Error = sptr->Last_Error;	// 更新前次误差
	sptr->Last_Error = iError;		  	// 更新上次误差
	
	return Increase;	// 返回增量
}

超声波检测障碍物

超声波发车和按键发车

左右灯，鸣笛

干簧管检测磁铁

自动停车

程序测试

待编辑......

滤波后的电磁循迹

思路

C=DCZ-DCY//差=电磁左-电磁右
当小车处于直道和弯道时，对小车打舵的灵敏度要求不一样，

PD控制舵机+滤波电磁循迹

PI控制速度+PD控制舵机+滤波

参考文献

【1】电磁循迹中的基本控制算法

【2】三天让车跑起来！stm32循迹车

【3】深入浅出PID控制算法：

【4】位置式PID与增量式PID区别浅析

【5】电磁车算法优化总结