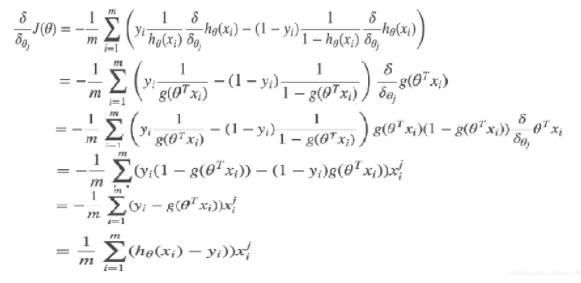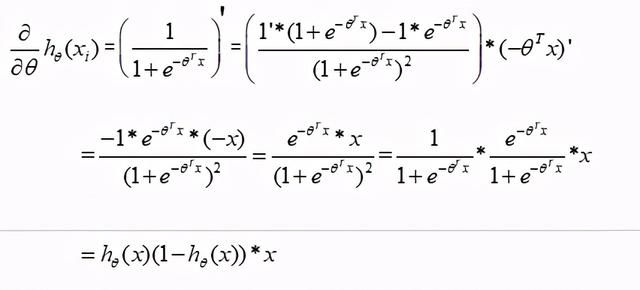正确率能很好的评估分类算法吗_人工智能入门算法逻辑回归学习笔记
逻辑回归是一个非常经典的算法,其中也包含了非常多的细节,曾看到一句话:如果面试官问你熟悉哪个机器学习模型,可以说 SVM,但千万别说 LR,因为细节真的太多了。
秉持着精益求精的工匠精神不断对笔记进行修改和改进,本着开源精神帮助大家一起学习。
Logistic Regression 虽然被称为回归,但其实际上是分类模型,并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。
Logistic 回归的本质是:假设数据服从这个分布,然后使用极大似然估计做参数的估计。
原理
如果直接将线性回归的模型扣到Logistic回归中,会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量,某个概率作为方程的因变量估计值取值范围为0-1,但是,方程右边取值范围是无穷大或者无穷小。所以,才引入Logistic回归。Logistic回归实质:发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。
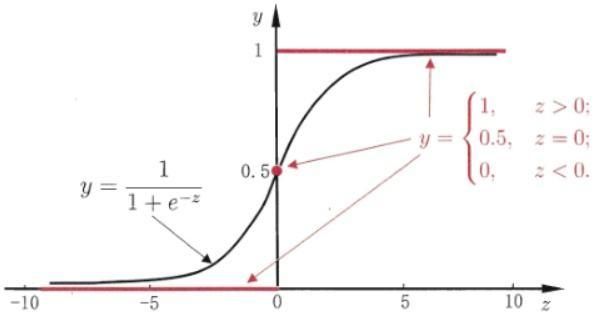
Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似,但是 Logistic 分布的尾部更长,所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在
的特殊形式。
求解
1. 梯度下降法
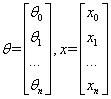
逻辑回归的公式为
其中:
则:
叫做预测函数,一般表示结果取1的概率,那么对于单条样本分类1和0的概率分别为:
可以整理成如下格式:
构造交叉熵损失函数(cost函数):
利用最大似然估计推导损失函数,最大似然估计就是利用已知的样本结果,反推能导致这样结果最大概率的一组参数值。举例:假设一个袋子中只装有未知数的黑球和白球,现在有放回的随机抽取球,做了一次测试,这次测试中抽取了10次,结果其中8次抽到了黑球,2次抽到了白球,假设抽到黑球的概率是p,那么抽到8次黑球和2次白球的概率为:,现在要求p是多少?
这里已经有了抽样10次,抽到了8次黑球,2次白球的样本结果,那么导致结果P最大概率下的p就是抽到黑球的概率。这里的思想就是最大似然思想。根据最大似然估计可知,由已知的样本结果(各个维度的值和分类的类别),反推导致这样结果出现最大概率的一组参数值(),可以取似然函数为:
两边取对数(单调性不变),将相乘转为相加:
对数似然函数为:
最大似然估计就是要求使取最大值时的一组。由于是凸函数,有极大值,可以乘以一个负系数,变成凹函数。得到逻辑回归的损失函数:
,现在只要求得
最小值时的那组
值,就是求得了满足最大似然函数最大的那组最佳值。现在只要求得
值。
利用梯度下降法求的最小值:
要求的
的最小值,只要求得满足
偏导为零时的那组
就可以。
补充:
通过将
来求解方程组,由于
参数的数量很多,得到最佳的一组
值不大现实。可以使用梯度下降法来求解方程组的值。根据梯度下降法可以得到的更新过程如下:
,
值代表学习步长。
表示
在t+1时刻的一组参数值,
表示
在t时刻的一组参数值,
表示在当前
下J随着
变化而变化的趋势,
总结:
就是
根据步长每次按照梯度下降的方向迭代寻找一组最合适的
使损失函数最小,这组
就是逻辑回归公式中最优的权重值。
逻辑回归优化
1. 有无截距
对于逻辑回归分类,就是找到z那条直线,不通过原点有截距的直线与通过原点的直线相比,有截距更能将数据分类的彻底。
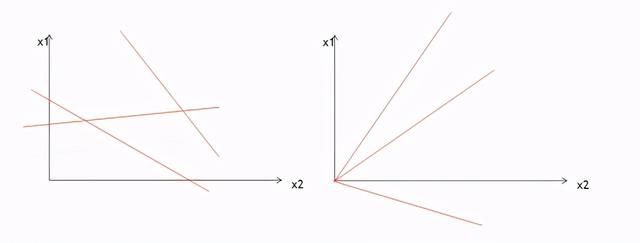
2. 线性不可分问题
对于线性不可分问题,可以使用升高维度的方式转换成线性可分问题。低维空间的非线性问题在高维空间往往会成为线性问题。
3. 调整分类阈值
在一些特定的场景下,如果按照逻辑回归默认的分类阈值0.5来进行分类的话,可能存在一些潜在的风险,比如,假如使用逻辑回归预测一个病人得癌症的概率是0.49,那么按照0.5的阈值,病人推测出来是没有得癌症的,但是49%的概率得癌症,比例相对来说得癌症的可能性也是很高,那么我们就可以降低分类的阈值,比如将阈值设置为0.3,小于0.3认为不得癌症,大于0.3认为得癌症,这样如果病人真的是癌症患者,规避掉了0.49概率下推断病人是不是癌症的风险。
降低阈值会使逻辑回归整体的正确率下降,错误率增大,但是规避了一些不能接受的风险。
4. 鲁棒性调优
鲁棒是Robust的音译,也就是健壮和强壮的意思,比如说,计算机软件在输入错误、磁盘故障、网络过载或有意攻击情况下,能不死机、不崩溃,就是该软件的鲁棒性,那么算法的鲁棒性就是指这个算法的抗干扰能力强。
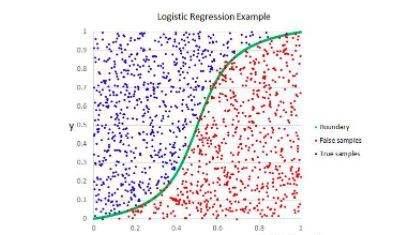
逻辑回归的决策边界
如下(当维度只有两个时,决策边界是一条直线):
如下两个模型:
第一个模型相对于第二个来说各个维度的权重相对来说小,当遇到数据有噪声时,抗干扰的能力强,数据扰动小。比如:当时,第一个模型结果为90.3,第二个模型结果为903。当有数据噪声时,第一个模型结果为94.3,数据扰动为4,第二个模型结果为943,数据扰动为40。
可见模型维度权重小的模型抗干扰能力强,并不是模型维度权重越小,模型越好,如果模型权重很小,很小,那么模型受各个维度值变化的影响非常小,只与参数有关,与其他维度的权重没有关系,所有训练数据和测试数据都会得到相同的结果,那就是欠拟合的状态。如果模型维度权重太大,维度又多,这种模型当数据改变一点,扰动也大,对训练数据拟合的好,当测试数据本身改变一点时,变化也大,反而成了一种过拟合的状态。
无论是欠拟合或者过拟合模型都无法泛化(模型能够应用到新样本的能力)到新的样本数据,无法预测准确的值。各个维度的值偏大容易过拟合(一般过多的维度特征,很少的训练数据集,容易导致过拟合出现),各个维度的值偏小容易欠拟合,可见维度的权重不能太大,也不能太小,如何得到一组比较合适的权重值?这里就需要使用正则化。
正则化主要是用来解决模型过拟合,实际上,模型参数的权重值越小,通常对应越光滑的函数图像,就不易发生过拟合问题。正则化中将保留模型中的所有的维度,会将各个维度的权重保持尽可能小的状态。有两种正则化:L1正则化和L2正则化,公式如下:
L1L2 正则化的区别:L1倾向于使所有的w要么取1,要么取0。L2倾向于使w整体偏小。由此可见,L1正则化对于参数为0的维度,可以直接舍去,起到降维的作用。
如何应用正则化?简单直观来看可以重写逻辑回归的误差函数为:ng
其中:
叫做正则化参数,一般设置不会超过1,0.3或者0.4最佳,不要太大.
我们训练模型目的是使E尽可能的小,E中的
越小代表训练出来的一堆参数能更好的拟合训练数据,代表我们训练的模型越准确,我们希望能够很好的拟合训练数据,但是不能过拟合,那么E后面惩罚项或者就是通过正则化项在保证得到的参数值较小,这里惩罚项可以说是代表模型的推广能力,也就是抗干扰能力。也就是说
在控制两者之间的平衡,可以通过
设置保证E尽可能小的情况下,既能保证训练出来的模型很好的拟合训练数据,又能保证得到的模型参数值保证在较小状态,不会发生过拟合。重写误差函数之后,误差就相对来说不大准确,正确率下降,但是相应地牺牲了正确率,提高了推广能力。
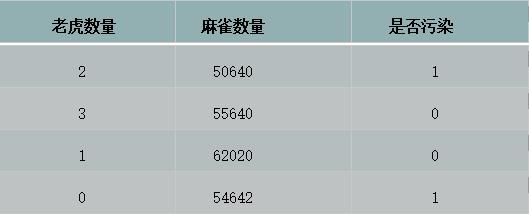
- 归一化数据
如图,要预测某区域是否污染,有两个维度特征:老虎数量和麻雀数量。这两个维度特征的量级不同,会导致训练出来模型中老虎这个特征对应的w参数大,而麻雀数量这个特征对应的w参数小,容易导致参数小的特征对目标函数的影响被覆盖,所以需要对每个特征的数据进行归一化处理,以减少不同量级的特征数据覆盖其他特征对目标函数的影响。
归一化数据可以使各个特征维度对目标函数的影响权重一致,提高迭代的求解的收敛速度。
最大最小值归一化:
缺点是抗干扰能力弱,受离群值影响比较大,中间容易没有数据。最大最小值归一化后的数据落在[0,1]之间。假设某个特征下有一组数据:1,2,3,4,5,100那么对数据使用最大最小值归一化后的值为:0,2/99,3/99,4/99,1。中间没有数据,受离群值100的影响大。
方差归一化:
方差归一化抗干扰能力强,和所有数据有关,求标准差需要所有的值介入,若有离群值,会被抑制下来。但是归一化后的数据最终的结果不一定落在0到1之间。
注意:理论上一个模型算法如果拿到训练集所有的特征一起训练模型就要归一化数据。决策树算法可以不归一化数据。
- 调整数据的正负值-均值归一化
逻辑回归中,梯度下降法迭代求的过程如下:
可以转换写为:
,在步长值确定的情况下,A是一个值,当x一组值为同号时,调整w参数只能朝着一个方向调节,要么使w0,w1,w2 参数朝着正方向调节,要么朝着负方向调节,如下图,假设由wt调节到wt+1,如果w只能朝着一个方向调节需要两步,如果由wt沿直线调节到wt+1只需要一步,但是这样就要向小的方向调节,需要向大的方向调节,这样就有了矛盾,如何解决矛盾?这里就需要使用均值归一化。
均值归一化是将原来的特征值减去这个特征在数据集中的均值,这样就会使x的各个维度取值上有正有负,在迭代求
参数时,能减少迭代的次数。
- 训练方法选择
训练逻辑回归的方法有:SGD和L-BFGS,两者的区别为:
SGD:随机从训练集选取数据训练,不归一化数据,需要专门在外面进行归一化,支持L1,L2正则化,不支持多分类。
L-BFGS:所有的数据都会参与训练,算法融入方差归一化和均值归一化。支持L1,L2正则化,支持多分类。