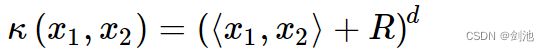AI 人工智能之常核函数

核函数

核函数(Kernel Function)，统计学术语，支持向量机通过某非线性变换 φ( x) ，将输入空间映射到高维特征空间。如果支持向量机的求解只用到内积运算，而在低维输入空间又存在某个函数 K(x, x′) ，它恰好等于在高维空间中这个内积，即K( x, x′) =<φ( x) φ( x′) > 。

核函数是讲计算低维的数据映射到高维的过程，这样在低纬度情况中线性不可分的情况，在高维度中可能线性可分。假设有一组数据，这组数据如果不是线性可分，那么如果可以用核函数的方法去计算低纬度的数据，仅仅通过计算低纬度的数据就能得到高维数据的内积信息，则极大的减小了计算的复杂量。

核方法只是一种处理问题的技巧，低维空间线性不可分可以在高维空间线性可分，但是高维空间的计算复杂度又很大，那么我们就把高维空间的计算通过低维空间的计算外加一些线性变换来完成。

假设函数Ф是一个从低维特征空间到高维特征空间的一个映射，那么如果存在函数K(x,z), 对于任意的低维特征向量x和z，都有：K(x,z)=θ(x)*θ(z),称函数K(x,z)为核函数。

核函数K就是指K(x, y) = ，其中x和y是n维的输入值，f(·) 是从n维到m维的映射（通常而言，m>>n）。是x和y的内积，严格来说应该叫欧式空间的标准内积，也就是很多人常说的点积。

本质上来说核函数是一个低纬的计算结果，并没有采用低纬到高维的映射。只不过核函数低纬运算的结果等价于映射到高维时向量点积的值。

要计算，需要先分别计算f(x)和f(y)，然后再求它们的内积。经过映射后的x和y，维数大大增加，计算内积的成本可能会非常大，而且在高位空间计算内积又费时费力，所以特别想要一个“简便运算法”，这就需要核函数了。

例如：
令 x = (x1, x2, x3, x4); y = (y1, y2, y3, y4)；
令 f(x) = (x1x1, x1x2, x1x3, x1x4, x2x1, x2x2, x2x3, x2x4, x3x1, x3x2, x3x3, x3x4, x4x1, x4x2, x4x3, x4x4)；f(y)亦然；
令核函数 K(x, y) = ()^2。
接下来，让我们带几个简单的数字进去看看是个什么效果：x = (1, 2, 3, 4)；y = (5, 6, 7, 8)。那么： f(x) = ( 1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16)；
f(y) = (25, 30, 35, 40, 30, 36, 42, 48, 35, 42, 49, 56, 40, 48, 56, 64)；
= 25+60+105+160+60+144+252+384+105+252+441+672+160+384+672+1024 = 4900。

f(x·y)把四维空间的数据映射到十六维空间里。计算内积非常复杂。

例如核函数 K(x, y) = (5+12+21+32)^2 = 70^2 = 4900。可以看出来核函数其实就是帮我们省去在高维空间里进行繁琐计算的“简便运算法”。

再例如：

有两个两维的向量，进行二阶多项式扩展，然后进行内积计算，这个时候映射高高维后计算的计算量为：11次乘法+4次加法；采用近似计算的计算量为：3次乘法+2次加法；采用加系数后的近似计算的计算量为：4次乘法+2次加法；

 核函数的满足条件: Mercer 定理：任何半正定的函数都可以作为核函数。所谓半正定的函数，是指拥有训练数据集合 ，定义一个矩阵的元素 ，这个矩阵是n×n的，如果这个矩阵是半正定的，那么 就称为半正定的函数。

常用的核函数

线性核函数，其实就是没有映射: 

高斯核函数，使用最为广泛，它能够把原始特征映射到无穷维。

多项式核函数，它能把数据映射到 维。

 选择什么样的核函数将会决定你把数据映射到什么样的维度。