用Python学《微积分B》（函数项级数）

  函数项级数（Series of Functions），借用WIKI上的定义：
  In calculus, a function series is a series, where the summands are not just real or complex numbers but functions.Examples of function series include power series, Laurent series, Fourier series, etc.
  也就是说，函数项级数的被加项是函数。幂级数、Laurent级数和Fourier级数都属于函数级数。

u1(x)+u2(x)+u3(x)+⋅⋅⋅=∑n=1∞un(x)

  从上面的表述来看，貌似函数项级数与常数项级数唯一的差别就是被加项不同，但是，如果从几何上，你会发现它们的差异非常之大：
1）常数项级数收敛几何上表现为：无穷多个数（点）相加的值逼近（收敛）于一个数，典型的如这个“box分割”图

2）函数项级数收敛几何上表现为：无穷多条曲线叠加后逼近（收敛）于一条曲线，例如“余弦函数叠加构造方波”

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 6 * np.pi, 1024)
y0 = 0.5 * np.ones(x.size) 
y1 = 0.673 * np.cos(x);
y2 = -0.212 * np.cos(3 * x)
y3 = 0.127 * np.cos(5 * x)
y = y0 + y1 + y2 + y3
plt.plot(x, y0, 'g:')
plt.plot(x, y1, 'y:')
plt.plot(x, y2, 'm:')
plt.plot(x, y3, 'c:')
plt.plot(x, y, 'r')
plt.show()

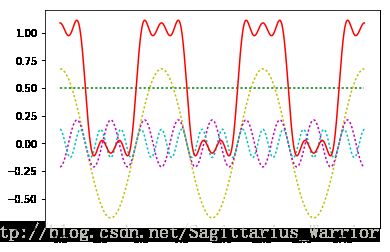
  如上图所示，各色虚线叠加后变成了红色实线。需要注意的时，这里仅仅为了演示，没有画无穷多条线。
  很显然，常数项级数收敛是点的收敛，而函数项级数收敛是线的收敛，后者比前者高了一个维度。对于函数项级数，只有站在曲线叠加的角度来看，才能很好地理解与之相关的各个概念，比如：和函数、一致收敛等。

一、和函数与一致收敛

1，和函数（sum function）与部分和（partial sum）
  本章的概念比较多，和函数是第一个关键概念。

S(x)=∑n=1∞un(x)=limn→∞∑k=1nuk(x)

注1：和函数存在的前提条件是 x∈I 时，该级数收敛。即只有在收敛的前提条件下讨论和函数才有意义。其中，I是一个区间，专业名称叫“收敛域”。
注2：上式右边是和函数，左边是部分和的极限，它反映了和函数与部分和的联系。
2，一致收敛（Uniform Convergence）和逐点收敛（Pointwise Convergence）
  WIKI - Uniform Convergence对这两个概念的解释比较到位。简单来说，逐点收敛并不能确保和函数是连续的，比如：

u1(x)=x,u2(x)=x2−x,⋅⋅⋅un(x)=xn−xn−1,∑n=1∞un(x)

S(x)=limn→+∞∑k=1nuk(x)=limn→+∞xn={0,1,x∈[0,1)x=1

  一致收敛，WIKI上形象的说：它要求 fn 不但要收敛于f，而且收敛的速度要一致。有没有想到什么？第一章的“函数连续和函数一致连续”！
  Loosely speaking, this means that fn converges to f at a “uniform” speed on its entire domain, independent of x.
  关于一致收敛， 同济版《高等数学》12-6节，从几何的角度来描述，感觉要容易理解得多。原话如下：
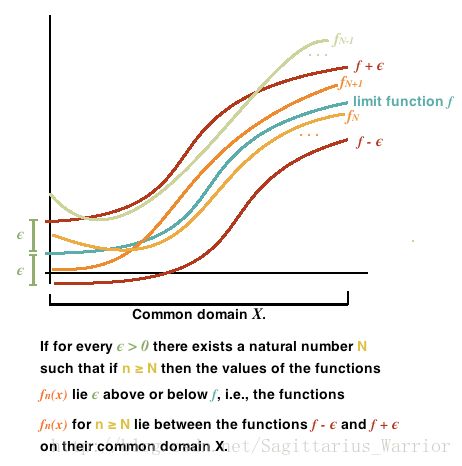
  只要 n 充分大 （ n > N ），在区间 I 上所有曲线 y=sn(x) 将位于曲线 y=S(x)−ϵ 与 曲线 y=S(x)+ϵ 之间，如下图

3，Cauthy一致收敛准则
  对于一致收敛，直接从定义来判断，比较麻烦，可以应用Cauthy收敛准则。不同的是，要将被加项由常数项改为函数。

|∑k=n+1n+puk(x)|<ϵ

  注：它要求的是收敛域中的所有x都满足上式，而不是某几个点 x0,x1,x2,... 。

二、一致收敛级数的分析性质

1，连续性
1）被加项连续，则收敛项也连续。

if"fn∈C(I)"and"{fn}→f"⇒"f∈C(I)"

2）被加项连续，则和函数连续

"fn∈C(I)"⇒"S(x)∈C(I)"

2，逐项可积

∫baf(x)dx=limn→∞∫bafn(x)dx

∫ba[∑n=1∞un(x)]dx=∑n=1∞∫baun(x)dx

注1：它的条件是 un(x) 连续，且级数一致收敛
注2：第一个式子反映的是：在这个条件下，积分和求极限可交互次序。
注3：第一个式子反映的是：在这个条件下，积分和求和可交互次序。
3，逐项微分

f′(x)=limn→∞f′n(x)

ddx[∑n=1∞un(x)]=[∑n=1∞ddxun(x)]

注1：它的条件除了一致收敛外，还要求 un(x)∈C′[a,b]
注2：第一个式子反映的是：在这个条件下，求导和求极限可交互次序。
注3：第一个式子反映的是：在这个条件下，求导和求和可交互次序。
注：以上性质在WIKI - Uniform Convergence和Uniform Convergence可以查到。

三、幂级数

1，一般形式
  幂级数（Power Series）的一般形式如下：

∑n=0∞an(x−c)n=a0+a1(x−c)1+a2(x−c)2+⋅⋅⋅

若 c = 0

∑n=0∞anxn=a0+a1x+a2x2+⋅⋅⋅

注：第二个式子又叫“Maclaurin Series”，后面没有特别说明，默认幂级数为Maclarin级数。
2，幂级数的收敛半径（Radius of convergence）
  任何幂级数（Maclarin Series）的收敛域一定是关于原点对称的区间
注：对于一般形式的，对称点是 x0
  根据Abel’s Theorem，幂级数的收敛性有三种情况：
1）当前仅当 x = 0 收敛，即收敛域为一个点。例如：

∑n=0∞n!xn

2）收敛域为 (−∞,+∞) ，例如：


3）收敛域为 (−R,R) ，收敛域外处处发散，例如：

∑n=0∞xn2n

  统一来说，R称为幂级数的收敛半径（Radius of convergence）。
定理

limn→∞|an+1an|=ρ,R=1ρ

limn→∞|an|−−−√n=ρ,R=1ρ

注：前者是比值法，后者是根值法。
例：求下列幂级数的收敛区间

∑n=0∞1n3nx2n+1

解：先变换

∑n=0∞1n3nx2n+1=x∑n=0∞1n3nx2n

再换元 u=x2

∑n=0∞unn3n

3，幂级数的分析性质
1）内闭一致收敛

b<R,[−b,b]

2）逐项求导后的幂级数收敛半径不变

∑n=1∞nanxn−1

3）幂级数的和函数在收敛半径内“连续”、“可导”，且有：

S′(x)=(∑n=0∞anxn)′=∑n=0∞(anxn)′=∑n=1∞nanxn−1=a1+2a2x+3a3x2+⋅⋅⋅+nanxn−1+⋅⋅⋅

注：这是逐项求导性质，有没有发现：求导过后，它还是一个幂级数，依次类推，可以一直求导下去。

∫x0S(t)dt=∫x0(∑n=0∞antn)dt=∑n=0∞∫x0antndt=a0x+a12x2+⋅⋅⋅+ann+1xn+1+⋅⋅⋅

这是逐项积分

四、函数的幂级数展开

1，重要推论
  从上面最后一个定理，可以得出一个推论：如果幂级数的收敛半径为R，则其和函数 S(x) 在 (-R,R) 中有任意阶导数

S(k)(x)=∑n=k∞n(n−1)⋅⋅⋅(n−k+1)anxn−k,k=1,2,3,...

且等式右边的幂级数的收敛半径也是R。
  利用逐项求导或逐项积分，可以由已知幂级数的和函数求出另外一些幂级数的和函数，反过来，也可以把一些初等函数展开为幂级数。这就是“函数的幂级数展开” 的理论基础，它实际上是求和函数的逆过程。
例如：由几何级数在收敛域 (-1,1) 的和函数 S(x)=11−x ，通过逐项积分，可以推导出 ln(1−x) 的展开式。
2，Taylor级数
  从“求和函数的逆过程”来看待“函数的幂级数展开”有一定的局限性——需要从已知和函数的级数出发去推导。那么，有没有一般的方法来判断一个函数是否能展开成幂级数？怎么展开？这种展开是唯一的吗？
答案是：有！这就是Taylor级数（Taylor Series）。

f(x)∼f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2+⋅⋅⋅+f(n)(x)n!(x−x0)n+⋅⋅⋅

  Taylor级数展开是通过“求n阶导”的方法，来确定如何将一个函数进行幂级数展开。很明显，要进行Taylor级数展开，那么首要条件就是这个函数要满足无穷阶可导。
  事实上，函数能够进行幂级数展开的充分条件：

|f(n)(x)|≤M

  不但要满足无穷阶可导，且导函数要有界。
3，Taylor级数与Taylor公式
  可以证明“函数的幂级数展开式是唯一的，正是Taylor级数”
  这就要从前面学的Taylor公式说起啦：

f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2+⋅⋅⋅+f(n)(x)n!(x−x0)n+Rn(x)

  上式右边也称为“Taylor多项式”。很明显，“Taylor多项式”比“Taylor级数”的条件要宽泛得多，前者只需要n阶可导（有限阶），后者需要无穷阶可导。
  在《微积分B》5-5节的课程中，扈老师是这样来证明（推导）Taylor公式的：先假设函数f(x)可以展开成一个多项式：

f(x)=C0+C1x+C2x2+⋅⋅⋅+Cnxn

  然后通过对上式在 x=a 这一点进行逐级求导，来确定系数数列 {Cn} 与 导数数列 {f(n)(a)} 之间的关系。
  最后证明函数f(x)与“Taylor多项式”的误差 ϵ=Rn(x)=o[(x−a)n+1]
  此外，通过反证法可以证明“Taylor多项式的唯一性”。
  从这个证明可以发现两点：
  1）Taylor多项式的适用范围是 a 点及其附近 （点的邻域）；
  2）f(x)与“Taylor多项式”的误差随着项数的增加而变小。
  对于第二条，可以想象一下，当项数 n→∞ 时，Taylor多项式不就变成了Taylor级数了吗？
  事实上，可以证明，如果

limn→+∞Rn(x)=0

  那么，f(x)就可以展开为Taylor级数。
  回过头来看第一条，Taylor多项式的适用范围是点的邻域，而Taylor级数是幂级数，它的收敛域是一个对称的区间。可以证明，Taylor级数收敛区间的对称点就是Taylor多项式的展开点。换个角度来看，Taylor级数是Taylor多项式的延伸，从点的邻域向两边延伸从一个连续的对称区间。
  同样地，可以证明“Taylor级数也是唯一的”，因为，函数的幂级数展开只能是Taylor级数展开。
4，Sympy - series expansions
  Sympy中专门设立了一章介绍级数展开。我在前面做Unit Test 3 时，已经用到了“Sympy Core -> Series Expansion”中的“series()”函数。
总结：手动进行“函数的幂级数展开”一般有这么两个方法：一是从已知和函数的级数进行变形、积分或求导得出；二是应用Taylor公式。常用的5个重要的“Maclaurin Series”要熟悉，一般的级数展开都是从这个5个级数展开变形来的。link

ln(1+x)=∑n=1∞(−1)n+1nxn,x∈(−1,1]

ex=∑n=0∞xnn!

sin(x)=∑n=0∞(−1)n(2n+1)!x2n+1

cos(x)=∑n=0∞(−1)n(2n)!x2n

(1+x)α=∑n=0∞α(α−1)⋅⋅⋅(α−n+1)n!xn,x∈(−1,1)

11+x=∑n=0∞(−1)nxn,x∈(−1,1)

11−x=∑n=0∞xn,x∈(−1,1)

注意：第五个公式又称为“二项式展开”，如果 α 取整数，就是中学代数中的二项式定理。

六、幂级数的应用

1，近似计算
  严格来说，这个是Taylor公式的应用。对于像三角函数、对数、带高次根的数（二项式展开， α 取分数），可以借助Taylor公式展开来近似计算，并可以根据需要的精度展开到k项（k阶导数）。例：

240−−−√5=35−3−−−−−√5=31−134−−−−−−√5

应用“二项式展开”，取 α=15,x=−134 ， 注意 x∈(−1,1) 。

from sympy import *
init_printing()
x = Symbol('x')
x = Symbol('x')
expr = (1 + x) ** (1 / 5)
for n in range(5):
    print(series(expr, x, 0, n+1))

1 + O(x)
1 + 0.2*x + O(x**2)
1 + 0.2*x - 0.08*x**2 + O(x**3)
1 + 0.2*x - 0.08*x**2 + 0.048*x**3 + O(x**4)
1 + 0.2*x - 0.08*x**2 + 0.048*x**3 - 0.0336*x**4 + O(x**5)


  Taylor公式的另一项重要应用是近似计算定积分。从几何上（面积）很容易理解这种近似：定积分就是求曲线与x轴在某区间上围成的面积。如果曲线不规则，那么这个面积就不方便计算。而幂级数则是用多条规则的曲线来叠加逼近，根据积分和求和在“一致收敛”时可以交互次序的特性，我们可以先算各项的定积分，再累加即可。例：

2π√∫120e−x2dx,∫10sin(x)xdx

  对于这类积分，都是先将被积函数展开，然后逐项积分，最后累加


2，解微分方程
  参考Wiki - Power series solution of differential equations和Series Solutions
3，证明Euler Formula
  中文的WIKI - 欧拉公式给出了三种证明，其中第一种就是Taylor公式证明。另外，Math is Fun : Euler Formula上的证明更有趣。

from sympy import *
init_printing()
n = Symbol('n', integer=True)
expr = n / factorial(n+1)
Sum(expr, (n, 1, oo)), Sum(expr, (n, 1, oo)).doit()

(∑n=1∞n(n+1)!,1)

n = Symbol('n', integer=True)
expr = (-1) ** n * n * (n + 1) / 2 ** n
Sum(expr, (n, 1, oo)), Sum(expr, (n, 1, oo)).doit()

(∑n=1∞(−1)n2−nn(n+1),−827)

#Exercise 8-5-1
n = Symbol('n', integer=True)
x = Symbol('x')
expr = x ** n / n
limit(expr.subs(n, n + 1) / expr, n, oo)

1

Sum(expr.subs(x,1), (n, 1, oo)).is_convergent(), Sum(expr.subs(x,-1), (n, 1, oo)).is_convergent()

(False,True)

#n = Symbol('n', integer=True)
#x = Symbol('x')
n, x = symbols('n x')
expr = E ** x
series(expr)

1+x+x22+x36+x424+x5120+O(x6)