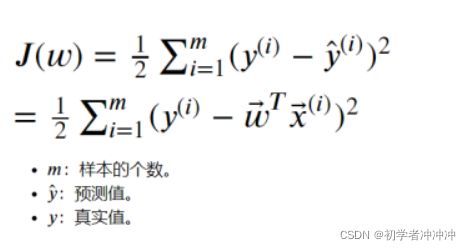一元线性回归实例和梯度下降应用及近期学习知识点总结 一月16日学习笔记

目录

线性回归

一元线性回归

损失函数

梯度下降

 利用梯度下降求线性回归函数：

 几个重要的概念（关于数据处理的）

 几个常用的库：

---

线性回归

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

一元线性回归

从上述定义中，我们可以知道，回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归称为一元线性回归分析，一元线性回归回归是的一种，评估的自变量X与因变量Y之间是一种线性关系。当只有一个自变量时，称为一元线性回归。

我们要知道理解什么是线性？，通俗的来讲就是我们求出来的图像是一条直线，自变量的最高次项为1，

拟合是指构建一种算法，使得该算法能够符合真实的数据。

从机器学拟合习角度讲，线性回归就是要构建一个线性函数，使得该函数与目标值之间的相符性最好。从空间的角度来看，就是要让函数的直线（面），尽可能靠近空间中所有的数据点（点到直线的平行于y轴的距离之和最短）。

线性回归模型：

例如我们有了一些房子面积和对应价格的数据，我们可以拟合一条直线，使其尽可能符合房子面积与价格的关系，（也就是是样本点都尽可能落在我们拟合的直线附近）

那么我们应该怎么拟合这条直线呢？我们首先要知道损失函数。

损失函数

 损失函数也称目标函数或代价函数，简单来说就是关于误差的一个函数。损失函数用来衡量模型预测值与真实值之间的差异。机器学习的目标，就是要建立一个损失函数，使得该函数的值最小。
也就是说，损失函数是一个关于模型参数的函数，自变量可能的取值组合通常是无限的，我们的目标，就是要在众多可能的组合中，找到一组最合适的自变量组合，使得损失函数的值最小。

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越小，通常模型的性能越好。不同的模型用的损失函数一般也不一样

通俗来讲就是，用数据的真实值去减去采用函数模型得到的预测值，计算的是一个样本的误差。它是用来估量你模型的预测值 f(x)与真实值 Y的不一致程度。

公式为 LOSS=真实值-预测值

对于一元线性回归而言。我们通常用均方差损失函数：

 我们有了损失函数我们又应该怎么求出它的最小值呢？这里1我们就要用到梯度下降法了。

梯度下降

        梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

 偏导：

在一元函数中，导数就是函数的变化率。对于二元函数的“变化率”，由于自变量多了一个，情况就要复杂的多。

在 xOy 平面内，当动点由 P(x0,y0) 沿不同方向变化时，函数 f(x,y) 的变化快慢一般来说是不同的，因此就需要研究 f(x,y) 在 (x0,y0) 点处沿不同方向的变化率。

在这里我们只学习函数 f(x,y) 沿着平行于 x 轴和平行于 y 轴两个特殊方位变动时， f(x,y) 的变化率。

偏导数的表示符号为:∂。偏导数反映的是函数沿各个坐标轴正方向的变化率。梯度的最大方向就是方向导数方向也就是数值变化最快的方向。

梯度下降；

我们可以用下山作为例子：（这里引用别人所举出的例子）

假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；

总之：通俗来讲就是利用当前位置的信息，一步一步迭代，找到最小值所在位置。

通过我们所学的高数知识知道，沿导数方向就是数值变化的最大方向。所以求导是必不可少的，就如同下山一样，我们有了下山方向就要考虑自己的下山所迈出的步伐，步长也是梯度下降中的一个重要参数，有了下山的方向也有了自己下山的步长，我们就可以一步一步进行一直到山底，也就是我们想要求出的函数中最小值点的参数。
下面是一维以及多维的示意图：

梯度下降一般步骤：

我们来看俩个具体的例子：(利用梯度下降求函数最低点)

  手工推导：

代码示例：

   一元情况：

import numpy as np
import matplotlib.pyplot as plt
plot_x=np.linspace(-1,6,141)   #在-1到6之间等距的生成141个数
 # 同时根据plot_x来生成plot_y
plot_y=0.5*plot_x*plot_x-2*plot_x+3
plt.plot(plot_x,plot_y)
plt.show()
###定义一个求二次函数导数的函数dJ
def dJ(x):
    return x-2

###定义一个求函数值的函数J
def J(x):
    try:
        return 0.5*x*x-2*x+3
    except:
        return float('inf')
x=0.0							#随机选取一个起始点
eta=0.1		#学习率
i=0
epsilon=1e-8				    #用来判断是否到达二次函数的最小值点的条件
history_x=[x]                   #用来记录使用梯度下降法走过的点的X坐标
while True:
    i=i+1
    d=0.5*x*x-2*x+3
    gradient=dJ(x)				#梯度（导数）
    last_x=x
    x=x-eta*gradient
    print("第%d次迭代 函数值%f x坐标%f 变化率%f"%(i,J(last_x),x,abs(J(last_x)-J(x))))
    history_x.append(x)
    if (abs(J(last_x)-J(x)) 

图像更替情况：

 二元情况：

    

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#定义x的导函数
def dJx(x):
    return 2*x-20
#定义y的导函数
def dJy(y):
    return 2*y-20
#定义求值函数
def z(x,y):
    return (x-10)**2+(y-10)**2
x=100.0
eta=0.1
i=0
k=0
y=100.0
epsilon=1e-8
historz_x=[x]
historz_y=[y]
m=z(x,y)
z1=[]
z1.append(m)
while True:
    i=i+1
    #dz=(x-10)**2+(y-10)**2
    gradientx=dJx(x)		#x梯度（导数）
    gradienty=dJy(y)
    last_x=x
    last_y=y
    x=x-eta*gradientx
    y=y-eta*gradienty
    print("第%d次迭代 函数值%f x坐标%f y坐标%f  变化率%f " %(i,z(last_x,last_y),x,y,abs(z(last_x,last_y)-z(x,y))))
    historz_x.append(x)
    historz_y.append(y)
    m=z(x,y)
    z1.append(m)
    if (abs(z(last_x,last_y)-z(x,y)) 

 图像变化情况：

 利用梯度下降求线性回归函数：

参数更新的主要步骤：

1.随机初始化一组参数θ

2.将目标函数J(θ)J(θ)分别对每个参数θ求偏导，（也可以理解为每个当前位置下山的最快方向）

3.用旧的值减去旧的值的导数乘于步长得到新的值。

θnew=θold-a *f'（θold）

a 为学习效率（也可以理解为下山的步伐）

b为每次迭代X的变化量  b=θold-θnew。

4.迭代次数一般通过2个参数控制

         初设的循环次数  或者 当b 也就是变化量小于一个特定的值。注意：a可以自己设定不易过大或过小，过大容易造成不准确，过小容易造成迭代次数过多。
下面看一个具体例子：（利用梯度下降求损失函数最小值点参数）

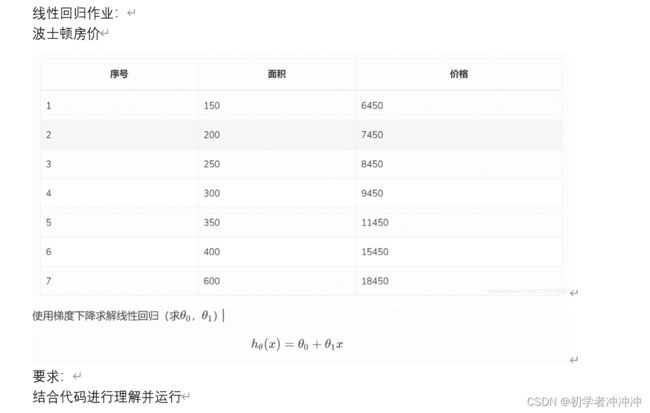
 下面继续看一个求线性回归的实例（一个作业）：

 代码实例

import math
m=7 #数据集大小
alpha=0.000001#学习率
area=[150,200,250,300,350,400,600];#数据集
price=[6450,7450,8450,9450,11450,15450,18450];
def gradientx(Theta0,Theta1):#对Theta0的偏导
    ans=0
    for i in range(0,7):
        ans=ans+Theta0+Theta1*area[i]-price[i]
    ans=ans/m
    return ans
def gradienty(Theta0,Theta1):#对Theta1的偏导0
    ans=0
    for i in range(0,7):
        ans=ans+(Theta0+Theta1*area[i]-price[i])*area[i]
    ans=ans/m
    return ans
def loss(Theta0,Theta1):  #损失函数
    ans=0
    for i in range(0,7):
        ans=ans+pow((Theta0+Theta1*area[i]-price[i]),2)
    ans=ans/(2*m)
    return ans
nowTheta0=1700  #设置的初始值
nowTheta1=60
print('处设置参数')
print(nowTheta0,nowTheta1)
#while math.fabs(nowTheta1-Theta1) >0.0000001 :#梯度下降
for i in range(500000):
    nowa=nowTheta0
    nowTheta0 = nowTheta0-alpha*gradientx(nowTheta0,nowTheta1)
    nowTheta1 = nowTheta1-alpha*gradienty(nowa, nowTheta1)
    if loss(nowTheta0,nowTheta1)<100.0:
        break
print('拟合参数')
print(nowTheta0,nowTheta1 )
import numpy as np
from matplotlib import pyplot
area=[150,200,250,300,350,400,600]#数据集
price=[6450,7450,8450,9450,11450,15450,18450]
pyplot.scatter(area,price)
x=np.arange(0,700,0.1) #随机生产X的值
y=nowTheta1*x+nowTheta0
pyplot.plot(x,y)
pyplot.xlabel('area')
pyplot.ylabel('price')
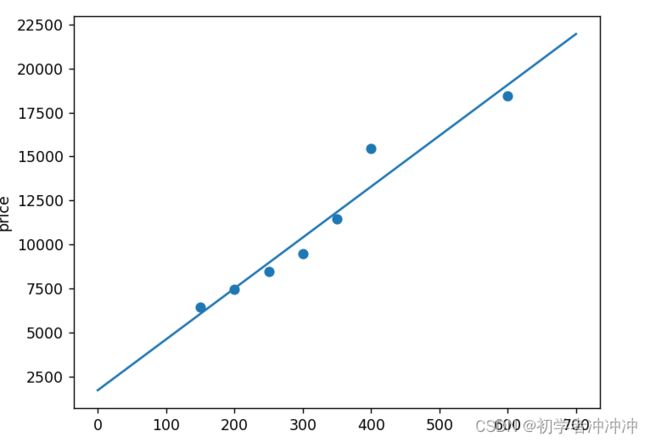
pyplot.show()

拟合结果： 

 几个重要的概念（关于数据处理的）

1.归一化：

2.标准化：

 3.正则化：

 详细介绍在这里（(1条消息) 正则化的理解_不曾走远的博客-CSDN博客_正则化）

 几个常用的库：

这里就不详细介绍以下库的用法了。

import pandas as pd             
import numpy as np  （用来处理数组矩阵）

常用numpy用法介绍（(1条消息) python学习笔记之numpy库的使用——超详细_逐梦er的博客-CSDN博客_如何导入numpy并命名为np）
import matplotlib.pyplot as plt（用来画图数据可视化）

 常用matplotlib库用法介绍（(1条消息) Python--Matplotlib（基本用法）_苦作舟的人呐-CSDN博客_matplotlib）