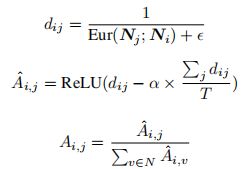读《Analyzing Unaligned Multimodal Sequence via Graph Convolution and Graph Pooling Fusion》

2020

摘要

融合视觉、语言、声音三模态
现有工作是集中在对齐融合单词，本文认为这是不切实际的
因此本文主攻非对齐模态序列的多模态序列分析的任务
常用的RNN系列网络由于其周期性，它们容易受到梯度消失/爆炸和高时间复杂度的影响

基于图的结构能够在时间维数上进行并行计算，并可以在较长的未对齐序列中学习更长的时间依赖性。
具体来说，这个多模态图是分层结构的，以满足两个阶段，即模式内和模式间的动态学习。
在第一阶段，对每个模态都采用图卷积网络来学习模态内dynamics（应该是相互作用的意思吧）。
在第二阶段，考虑到多模态序列是不对齐的，通常认为的词级融合不适用。为此设计了一个图池融合网络来自动学习来自不同模式的不同节点之间的关联。此外，我们还定义了多种方法来构造顺序数据的邻接矩阵。

引言

本文是用视频里的这三模态来推断说话者的情绪

在多模态序列分析的任务中，存在两个基本的挑战，即学习每个模态的模态内动态，以及捕获跨模态交互作用[2]的模态间对应物。（也就是说这个领域关注于区分intramodal和intermodal已经很久了吧）
该领域常用的RNN系列网络由于在时间维度上的递归性，在推理过程中速度较慢。它们还容易出现梯度消失/爆炸的问题，并且学习长期依赖[9]的能力有限，这增加了应用于模态间、模态内dynamics学习的难度。尤其对于未对齐的多模态序列分析，学习更长的时间依赖性具有重要意义，因为未对齐的序列通常都很长。

不同模态之间的交互通常更复杂，持续时间超过一个单词，即单词之间可能发生交叉模态交互，词级融合可能会将完整的交互分解成多个部分（其实就是说词级融合就是一一对应的双射吧，然后作者是要提出全连接的，那也就是说这个领域也是首次提出这种异构全连接吗）。此外，字级融合要求多模态序列在字级上严格对齐。然而，在现实场景中，序列通常不对齐，因为这种对齐是耗时间和计算昂贵的[12]（这个对齐align是什么意思，就是指双射吗，看其他领域全连接也会用对齐这个词啊）。因此，我们认为融合策略应该能够动态地关联来自多个模态的不同时间步长，而不是考虑每个特定时间步长的跨模态交互。

采用GCN替代RNN来处理单模态，提到GCN通过卷积学习节点相关性（但其实是个低通滤波器，并不是CNN那种小卷积核，而是一个大的“线性变换”算子），且不需递归可以并行提高效率（就是不同于GNN通过递归更新节点表示，通过与邻接矩阵和学习参数内积来更新）。更具体的是本文是采用有平均池化的graphsage，将每个时间步长视为一个节点，并将相关节点关联起来，即使它们在时间维数上相距很远，也可以学习到更长的时间依赖性

将图卷积应用于序列学习的一个主要障碍是序列没有像图结构数据那样的邻接矩阵。因此，邻接矩阵的识别和推导是很重要的（就是需要来个构图）。在本文中，我们提出了多种方法来实现这一目标，包括非参数的方法和可学习的方法。在非参数的方法下，我们主要研究了所提出的矩阵的有效性，即广义对角矩阵，它非常快，几乎无需计算。在可学习的方式中，我们通过梯度下降或节点相似性（跨节点注意）自动学习邻接矩阵，它更强大和表达能力。我们在实验部分给出了所提出的邻接矩阵的比较结果。

为了解决第二个问题，即模态间动态学习，我们精心设计了一个图池融合网络(GPFN)，它通过图池来学习聚合来自不同模态的各种节点。首先通过数学推导分析了均值/最大图池方法的合理性。然而，平均/最大图池仍然受到一些限制，因为它们是不可学习的，只能融合相邻的节点（其实就是池化、卷积这两种不同的下采样方式的区别呗）。因此，为了以更具表现力的方式融合节点，我们进一步提出了一种池策略，称为链接相似池，与平均/最大池相比，该策略能够考虑每个两个节点的共同邻居的关联分数。这种可学习的方法基于以下两个假设，即(i)两个节点的邻居明显重叠，则相似或紧密相关；(ii)如果两个节点是邻居，它们具有很高的可积可能性。因此，链接相似度池自动更新邻接矩阵和节点嵌入，以学习高级图表示。

相关工作

多模态序列分析

多模态序列分析属于多模态机器学习[19]和多视图学习[8]、[20]、[21]的交叉领域，近年来引起了广泛的研究兴趣。以往的工作集中于学习各种融合策略，以探索跨模态（跨视图）交互。探索跨模态交互的最简单的方法之一是在输入特征级别上连接特征（像素层或特征层吗），这表明它比单模态[22]-[25]有改进。相比之下，大量的出版物首先根据每种模式来推断决策，并使用一些投票机制[26]-[29]将来自所有模式的决策结合起来（决策层融合）。然而，正如Zadeh等人[2]所阐述的，这两种方法不能有效地建模模态间交互（那你这才是特征层融合？还是说视作第四类融合方式？）。

基于张量的融合受到了广泛关注。张量融合网络(TFN)[2]和低秩模态融合(LMF)[31]采用外积来学习三种模态的联合表示（那就是数学意味上的咯）。最近，Mai等人[33]提出了一种“分裂、征服和联合”的策略来进行局部和全局的融合。同样，建立了层次多项式融合网络(HPFN)[34]，通过多线性融合将其递归整合局部相关并传输到全局相关中。此外，一些翻译方法，如多模态循环翻译网络(MCTN)[35]和多模态变换器[36]，旨在通过将源模态转换为目标模态来学习联合表示（就是那种自编码器式的投影映射一样的交互吧）。Mai等人的[37]提出使用对抗性训练来翻译不同模态的分布，并使用一个将每个模态视为一个节点的图融合网络来融合模态。相比之下，我们的多模态图将每个时间步长视为一个节点，分别使用图卷积和图池来聚合信息和融合节点。此外，一些方法[38]，[39]使用因式分解方法来学习跨模态交互。应用跨模态注意机制(CIA)[40]、多任务学习(MTL)[41]和多逻辑网络[6]来探索多模态动力学等方法也非常流行

为了避免讽刺和歧义，多模态语言分析的主流是在单词层面上学习交叉视图交互，这样各种模态就会在时间维度[1]、[10]、[42]-[44]上对齐（就是双射了）。例如，记忆融合网络(MFN)[8]使用LSTM系统来学习模块内动力学，并实现增量记忆注意和多视图门控记忆网络来融合lstm的记忆，探索跨时间的模态动力学。Graph-MFN[11]通过使用一个简单的动态融合图来扩展MFN。虽然Graph-mfn采用了图网络，但它与我们的模型有很大的区别。
首先，动态融合图不跨时间融合特征，只是将每个模态视为一个节点，在同一时间段融合特征，而我们将每个时间步长视为一个节点，并在节点嵌入上进行图卷积（就是说人家的模型是把一个对象的每个模态整体看做一个节点吗，然后本文是一个模态有若干个时间步长对应若干个节点组成一个图吗）。其次，我们采用了图卷积和图池化这两种不涉及的跨模态融合操作。
多注意循环网络(MARN)[45]是为人类通信理解而开发的，利用多注意块发现随时间变化的多模态动态。此外，反复参与变异嵌入网络(raven)[7]通过基于音频和视觉线索的特征改变单词表示来建模多模态语言。然而，在现实场景中更实用也更具挑战性的非对齐的多模态序列中，不能执行字级融合。

我们的多模态图方法的明显区别在于，我们没有应用任何RNN或TCN变量来学习模态内和模态间交互，相反，我们研究了GCN探索多模态序列信号的有效性。我们的多模态图非常优雅和有效，通过直接关联远程相关节点，可以有效地学习更长的时间依赖性，并允许在时间维数上进行并行计算。

GNN

在所有这些GCN模型中，那些试图学习或恢复邻接矩阵的模型与我们的方法密切相关（原来是做矩阵补全吗）。[49]使用双级程序首先采样邻接矩阵，然后通过最小化内部和外部目标来学习图的参数（既视感）。相反，在直接学习的方式中，我们将邻接矩阵参数化为一个可学习的矩阵，并通过梯度下降联合学习邻接矩阵和图参数（nb）。此外，我们还提供了更多的定义邻接矩阵的方法。对于图池，DiffPool[50]使用节点嵌入来学习节点的可微软集群策略，并将节点映射到一组集群。相反，我们利用邻接矩阵来学习节点的聚类分配矩阵，它考虑了节点的链路相似性。与使用节点嵌入来学习聚类分配矩阵相比，使用邻接矩阵更直观和简单。结构池[51]利用条件随机场捕获不同节点之间的高阶结构关系，学习基于节点特征的节点簇分配矩阵，其中利用邻接矩阵寻找图的拓扑信息。相反，我们直接利用邻接矩阵中的链路信息来学习聚类分配矩阵。

方法

(明明是GCN还要贴聚合邻居和更新节点表示分开的公式？GCN里这两步不是直接AXW就完事了吗？)

单模态

通过核心是内积的注意力来确定各单模态的邻接矩阵（果然还是靠相似度，不过加了个可学习的注意力还好）

其中，$Q=f(W_{q}N)\in R^{T\times d}$、$P=f(W_{p}N)\in R^{T\times d}$
$W_1、W_2、W_q、W_p\in R^{d\times d}$是可学习矩阵
f是激活函数，R表示矩阵转置运算（不规范啊，大家都是用的T）。在所有方程中都应用ReLU作为激活函数，这样就可以有效地过滤掉节点之间的负链接（负链接这个解释，还是看这里的特殊性吧，这里就是在学习一个邻接矩阵，所以激活函数的输入就代表邻接矩阵中对应的连接）。
这样的邻接矩阵时间序列既是可学习的参数，同时也是实例（妙啊），因为它考虑节点之间的各种关系（时间步长），而不是直接设置所有矩阵元素可学习参数（将在第四节中讨论）。因此，本文称这种方法为间接学习。这种区别于实例的和可学习的方法可以在节点上捕获更多的相关性信息，从而可以产生更有利的性能，如第七节-D2节所示。

即使两个节点在时间维上距离较远，如果认为它们是相关的，它们仍然可以直接连接。因此，与RNN变体相比，GCN可以以更少的层有效地学习长期的时间依赖性，这使其成为学习长时间序列的合适选择。
虽然间接学习方法在避免递归和学习长期依赖方面与transformer[53]有一定的相似之处，但它在几个方面有所不同（果然现在提到GCN就得联动一下无敌的transformer了）。首先，transformer使用softmax作为激活函数，即每个时间步长都与所有的时间步长相关联。相比之下，我们的方法更有针对性，因为它能够过滤出没有直接连接的时间步长，并自动检测每个节点的一跳邻居（就是说transformer本质上是全连接，而GCN会有邻接矩阵过滤一下，但是transformer里的自注意力也在学这个关联性啊）。此外，在找到每个时间步长的邻居后，我们使用GIN[13]等GCN来聚合邻居的信息，该操作可以与变压器的前馈网络完全不同（那确实）。

另外强调本文的邻接矩阵值是连续的加权邻接矩阵

在实际应用时比较了图同构网络(GIN)[13]、图注意网络(GAT)[54]、GraphSAGE[18]和DiffPool[50]的性能。最后使用有平均池化的GraphSAGE[18]作为默认GCN，GraphSAGE第k次迭代的方程如下所示：

其中度矩阵左归一化
三模态的最后输出拼接起来再通过一线性层

跨模态

考虑到我们关注的是未对齐的多模态序列，因此无法实现常见的词级融合。这意味着我们的融合网络应该从多种模态中学习不同节点（时间步长）之间的相互作用，而不是在每个特定的时间步长中融合三种模态的特征。

与其他主要利用节点嵌入来学习聚类分配矩阵[50]、[51]的图池方法不同，我们提出利用邻接矩阵的链路信息来学习聚类分配矩阵，这更直观、更容易解释。

节点顺序

（因为并不是双射对齐式的，所以随意了？）

跨模态图池化

由于来自不同模态的特征是高度异构的，因此跨模态节点之间的相互作用比来自单一模态的节点之间的相互作用要复杂得多。因此，我们通过图池来学习单峰序列之间的相互作用。通过这种方式，该模型可以通过关联这三种模式之间的相关节点，自动学习异构模式之间的复杂的相互作用。

提供了两种聚合方法来聚合节点。第一种是简单的最大池和平均池。对于邻接矩阵，采用二维均值/最大池化，而对于节点嵌入，采用一维均值/最大池化

平均/最大池是有意义的，因为多模态序列的节点连接根据每个单峰序列的时间维度，因此相邻的节点密切相关的时间维度和被认为是可融合的（但我们需要仔细确定池大小s以避免融合节点从不同的模式）

同时数学推导这种池化的合理性，但这仍然不是未对齐的多模态序列中融合来自不同模态的节点的理想方法

链接相似性池

于是利用邻接矩阵中的链路信息（拓扑信息）来学习节点聚类分配矩阵。

与使用节点嵌入来学习集群分配矩阵的DiffPool[50]不同，使用邻接矩阵更直观和可解释性。
$Z^{\prime }=A{A}^T$
$Z=f[(Z^{\prime }+A)W_Z]$
Z是最终的节点簇分配矩阵，它将T个节点映射到T’个节点（那就是说并不是全连接，而是有限定连接个数？）
如果一对节点在其共享的邻居上具有相似的关联强度分布，那么就会导致更大的分数。同样值得注意的是，这个分数是加权的，因为邻接矩阵中的元素是软的（连续的）（原来很多地方提到的soft是连续的意思吗？），并且不被限制为二进制的。
$S=f(N{W}_S)$
$N_{update}=Z^{T}S$
$A_{update}=Z^{T}AZ$（这里就是DIFFPOOL吧，公式很像）

不使用节点嵌入的原因是邻接矩阵最初是来自于节点嵌入的，因此邻接矩阵包含了节点嵌入中的部分信息和拓扑信息。从而假设使用邻接矩阵就足以学习节点簇矩阵（那到底足不足以呢？）

其他构造邻接矩阵的方法

广义对角矩阵

相邻的时间片之间的关系更强

巨大优势：避免了寻找邻接矩阵的复杂计算。
实际上，GDM的函数就像TCN[16]、[17]、[55]中的内核，但与TCN内核不同的是，它是预定义的，而不是通过学习获得的(我们将学习部分留给GCN的参数)。GCN和TCN之间的主要区别将在第v节中讨论。此外，我们还实现了一个全连通邻接矩阵，它的值都是1个值来进行比较。与间接学习方法相比，该GDM方法具有直观性，符合序列建模的经验模式，但它既不是实例特有的，也不是可学习的。GDM是探索序列数据邻接矩阵的合理基线。

KNN

α是一个标量，它可以控制弱链接可以被过滤掉的程度。

直接学习

（真就直接学习这个邻接矩阵）

这个目标函数第一项强制每个节点的链接值之和等于零，这可以防止学习到的矩阵成为全连通矩阵（避免全连接？防止边太密吗？）。第二项限制每个节点的正链接值的和近似于给定的正标量γ，以防止其退化为全零矩阵。
通过梯度下降进行优化。请注意，学习到的邻接矩阵是在实例之间共享的（与实例无关的），与依赖于实例的学习方法相比，这可能不够表达力，但在计算上效率很高。

连接到tcn

TCN和GCN的区别：

可以看出（TCN还是很纯正的CNN啊，传统的傅里叶式卷积），TCN和GCN的主要区别是，TCN中的滤波器f共享序列的所有时间步(独立于t)，而GCN中的每一行对应一个节点（时间步），通常随不同的节点而变化。
换句话说，A对每个时间步都更可解释和具体，因此更具有代表性。此外，卷积滤波器f可以通过梯度下降自动学习，而A可以通过经验预定义（高下立判啊，肯定学习比预定义更有说服力啊？）。此外，在GCN中，如果A中对应的元素为正，我们可以通过A连接两个遥远的节点（时间步长）。通过这种方式，长期依赖可以有效地学习。相比之下，虽然扩张的时间卷积[16]也可以通过扩展卷积将两个遥远的时间步长与低层连接起来，但它是不灵活的，不能自动学习长期连接，因为扩张的时间卷积中的扩张速率必须手动预定义。

邻接矩阵中软权值的应用的论证

问题：如果使用二进制邻接矩阵（就是无权的邻接矩阵），GCN层的权值能否补偿邻接矩阵的二进制性质，并在内部缩放它们？换句话说，真的有必要在邻接矩阵中使用软权值吗？

本节是数学推导这邻接矩阵和权值如何相互作用，说明使用软权值的优势。

实验

基线

3)张量融合网络(TFN)[2]：TFN采用外部乘积来学习三种模态的联合表示，可以有效地保持单峰动力学，探索双峰和三峰的相互作用。TFN不是一种词级对齐融合方法，它可以处理未对齐的多模态序列，因为在融合前将单峰序列总结为单峰向量。