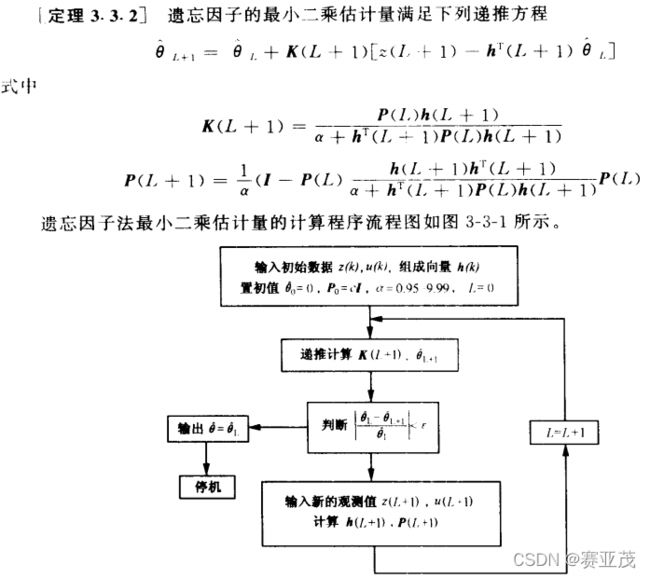
系统辨识的最小二乘法原理及其算法实现
1.原理
2.最小二乘法算法
3.最小二乘法递推算法
4.例题(Matlab实现)
clc,clear;close all;
rng(1)
%下面是系统的真实参数
a1 = -1.3;a2 = 0.7;
b0 = 1;b1 = -0.5;
%下面是采样点的数目:
num = 10000;sigma = 1;
%下面产生误差
e = normrnd(0,sigma,[num,1]);
%下面产生u,y(阶跃响应)
u = [zeros(round(num/10),1);ones(num - round(num/10),1)];
%u = ones(num,1);
y = zeros(num,1);
y(1) = 0;y(2) = 0;
for k = 3:num
y(k) = -a1*y(k-1)-a2*y(k-2)+b0*u(k)+b1*u(k-1)+e(k);
end
%下面将用最小二乘法递推算法求解参数
theta = [0 0 0 0]';theta_array = [theta];
P = sigma^2*eye(4);%PN的阶数
for k = 3:num
phi = [-y(k-1) -y(k-2) u(k) u(k-1)]';
G = P*phi/(1 + phi'*P*phi);
P = P - G*phi'*P;
theta = theta + G*(y(k) - phi'*theta);
theta_array = [theta_array,theta];
end
%下面开始画图
numbers = size(theta_array,2);
subplot(221);
box on;hold on;grid on;
plot(1:numbers,theta_array(1,:),'b-',1:numbers,ones(1,numbers)*a1,'r-');
xlabel('次数');ylabel('a_1');
title(['a_1相对误差:',num2str((a1 - theta_array(1,end))/a1*100),'%']);
subplot(222);
box on;hold on;grid on;
plot(1:numbers,theta_array(2,:),'b-',1:numbers,ones(1,numbers)*a2,'r-');
xlabel('次数');ylabel('a_2');
title(['a_2相对误差:',num2str((a2 - theta_array(2,end))/a2*100),'%']);
subplot(223);
box on;hold on;grid on;
plot(1:numbers,theta_array(3,:),'b-',1:numbers,ones(1,numbers)*b0,'r-');
xlabel('次数');ylabel('b_0');
title(['b_0相对误差:',num2str((b0 - theta_array(3,end))/b0*100),'%']);
subplot(224);
box on;hold on;grid on;
plot(1:numbers,theta_array(4,:),'b-',1:numbers,ones(1,numbers)*b1,'r-');
xlabel('次数');ylabel('b_1');
title(['b_1相对误差:',num2str((b1 - theta_array(4,end))/b1*100),'%']);
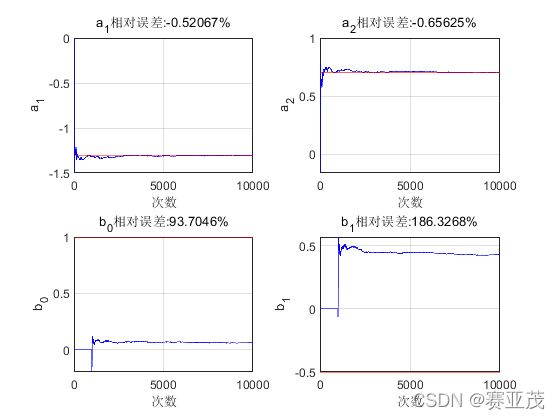
可以看出对 b 0 , b 1 b_0,b_1 b0,b1的识别不太好。
5.带遗传因子最小二乘递推法
function theta_array = Ff_minsquare(u,z,n,m,alpha,epsilon)
%u:输入值列向量 %n:分母的最高系数n
%z:输出值列向量 %m:分子的最高系数m
%h0:h初值 %theta0:theta初值
%algha:遗忘因子 %epsilon:阈值
theta = zeros(n+m+1,1);
C = 100;P = C*eye(n+m+1);
theta_array = [theta];
max_num = max(n,m) + 1;
numbers = size(u,1);
for k = max_num:numbers
theta_orgin = theta;
h = [-z((k-1):-1:(k-n));u(k:-1:(k-m))];
K = P*h/(alpha + h'*P*h );
P = 1/alpha*(eye(size(h,1)) - K*h')*P;
theta = theta + K*(z(k) - h'*theta);
theta_array = [theta_array,theta];
if norm(theta - theta_orgin)/norm(theta_orgin)<epsilon
break;
end
end
end
测试代码:
clc,clear;close all;
%下面是系统的真实参数
a1 = -1.3;a2 = 0.7;
b0 = 1;b1 = -0.5;
%下面是采样点的数目:
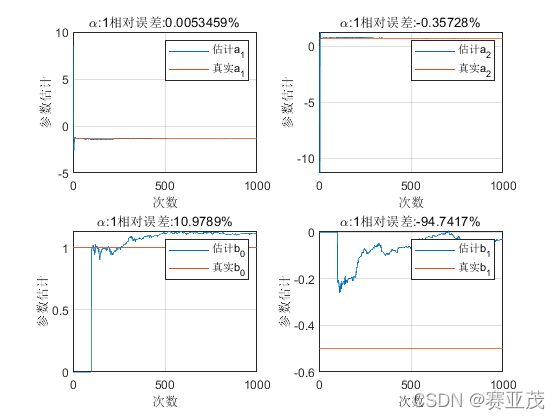
num = 1000;sigma = 1;alpha = 1;
%下面产生误差
e = normrnd(0,sigma,[num,1]);
%下面产生u,y(阶跃响应)
point = num/10;
u = [zeros(round(point),1);ones(num - round(point),1)];
y = zeros(num,1);
y(1) = 0;y(2) = 0;
for k = 3:num
y(k) = -a1*y(k-1)-a2*y(k-2)+b0*u(k)+b1*u(k-1)+e(k);
end
%下面将实现带遗忘因子的最小二乘法
theta_array = Ff_minsquare(u,y,2,2,alpha,1e-10);
%下面开始画图
cols = size(theta_array,2);
subplot(221)
box on ; grid on ; hold on;
plot(1:cols,theta_array(1,:),...
1:cols,a1*ones(1,cols));
xlabel('次数');ylabel('参数估计');
legend('估计a_1','真实a_1');
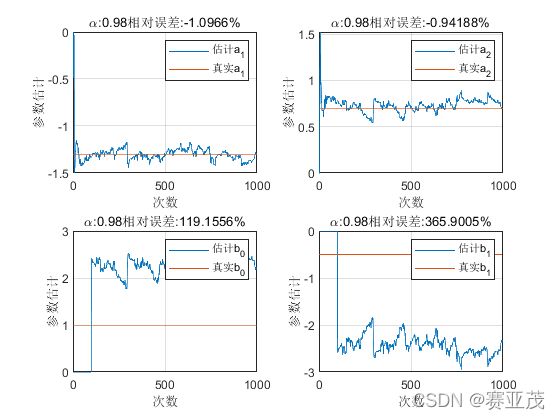
title(['\alpha:',num2str(alpha),...
'相对误差:',num2str((theta_array(1,end) - a1)/(a1)*100),'%']);
subplot(222)
box on ; grid on ; hold on;
plot(1:cols,theta_array(2,:),...
1:cols,a2*ones(1,cols));
xlabel('次数');ylabel('参数估计');
legend('估计a_2','真实a_2');
title(['\alpha:',num2str(alpha),...
'相对误差:',num2str((theta_array(2,end) - a2)/(a2)*100),'%']);
subplot(223)
box on ; grid on ; hold on;
plot(1:cols,theta_array(3,:),...
1:cols,b0*ones(1,cols));
xlabel('次数');ylabel('参数估计');
legend('估计b_0','真实b_0');
title(['\alpha:',num2str(alpha),...
'相对误差:',num2str((theta_array(3,end) - b0)/(b0)*100),'%']);
subplot(224)
box on ; grid on ; hold on;
plot(1:cols,theta_array(4,:),...
1:cols,b1*ones(1,cols));
xlabel('次数');ylabel('参数估计');
legend('估计b_1','真实b_1');
title(['\alpha:',num2str(alpha),...
'相对误差:',num2str((theta_array(4,end) - b1)/(b1)*100),'%']);