数值积分-求积公式余项,牛顿-柯特斯公式,辛普森公式,复合梯形公式,复合辛普森公式
文章目录
- 1.求积公式余项
-
- 1.1 定义
- 1.2 Python实现求积公式余项
- 2.牛顿-柯特斯公式
-
- 2.1 定义
- 2.2 Python实现牛顿-柯特斯公式
- 3.复合梯形公式
-
- 3.1 定义
- 3.2 Python实现复合梯形公式
- 4.复合辛普森公式
-
- 4.1 定义
- 4.2 Python实现复合辛普森公式
- 5.测试
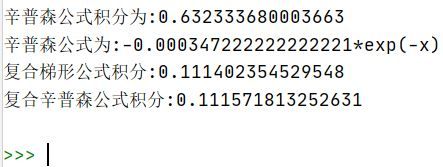
- 6.运行结果
1.求积公式余项
1.1 定义
R [ f ] = ∫ a b f ( x ) d x − ∑ k = 0 n A k f ( x k ) = K f ( m + 1 ) ( η ) , ( 1 ) R[f]=\int_a^b\!\!\!f(x)\mathrm{d}x-\sum_{k=0}^nA_kf(x_k)=Kf^{(m+1)}(\eta ),(1) R[f]=∫abf(x)dx−k=0∑nAkf(xk)=Kf(m+1)(η),(1)
其中 K 为不依赖 f ( x ) 的待定参数 , η ∈ ( a , b ) . 其中K为不依赖f(x)的待定参数,\eta \in (a,b). 其中K为不依赖f(x)的待定参数,η∈(a,b). 这个结果表明当 f ( x ) 是次数小于等于 m 的多项式时 , 这个结果表明当f(x)是次数小于等于m的多项式时, 这个结果表明当f(x)是次数小于等于m的多项式时,
由于 f ( m + 1 ) ( x ) = 0 , 故此时 R [ f ] = 0 , 即求积公式 ∫ a b f ( x ) d x ≈ ∑ k = 0 n A k f ( x k ) 由于f^{(m+1)}(x)=0,故此时R[f]=0,即求积公式\int_a^b\!f(x)\mathrm{d}x\approx\sum\limits_{k=0}^nA_kf(x_k) 由于f(m+1)(x)=0,故此时R[f]=0,即求积公式∫abf(x)dx≈k=0∑nAkf(xk)
精确成立 . 而当 f ( x ) = x m + 1 时 , f ( m + 1 ) ( x ) = ( m + 1 ) ! , ( 1 ) 式左端 R n ( f ) ≠ 0 , 故可求得 精确成立.而当f(x)=x^{m+1}时,f^{(m+1)}(x)=(m+1)!,(1)式左端R_n(f)\neq 0,故可求得 精确成立.而当f(x)=xm+1时,f(m+1)(x)=(m+1)!,(1)式左端Rn(f)=0,故可求得
K = 1 ( m + 1 ) ! [ ∫ a b x m + 1 d x − ∑ k = 0 n A k x m + 1 ] = 1 ( m + 1 ) ! [ 1 ( m + 2 ) ( b m + 2 − a m + 2 ) − ∑ k = 0 n A k x m + 1 ] \begin{aligned} K&=\frac{1}{(m+1)!}\left[\int_a^b\!\!\!x^{m+1}\mathrm{d}x-\sum_{k=0}^nA_kx^{m+1}\right]\\ &=\frac{1}{(m+1)!}\left[\frac{1}{(m+2)}(b^{m+2}-a^{m+2})-\sum_{k=0}^nA_kx^{m+1}\right] \end{aligned} K=(m+1)!1[∫abxm+1dx−k=0∑nAkxm+1]=(m+1)!1[(m+2)1(bm+2−am+2)−k=0∑nAkxm+1]
1.2 Python实现求积公式余项
from sympy.abc import x
from sympy import integrate, exp, diff
import numpy as np
from math import factorial
def quadrature_reminder(a, b, equal_segment, m, intergrand, a_k: np.ndarray):
"""
实现[a,b]代数精度为m的求积公式余项表达式
:param a: 区间左端点即起点a
:param b: 区间右端点即终点b
:param equal_segment: 区间等分数n
:param m: 代数精度m
:param intergrand: 被积函数f(x)
:param a_k: 权系数Ak数组
:return: 求积公式余项表达式
"""
step_h = (b - a) / equal_segment
f_x = x ** (m + 1)
f_x_k_array = np.array([f_x.subs(x, a + k * step_h) for k in range(equal_segment + 1)])
return 1 / factorial(m + 1) * (1 / (m + 2) * (b ** (m + 2) - a ** (m + 2)) - np.sum(a_k * f_x_k_array)) * diff(
intergrand, x, m + 1), a, b
2.牛顿-柯特斯公式
2.1 定义
设将积分区间 [ a , b ] 分为 n 等分 , 步长 h = b − a n , 选取等距节点 x k = a + k h 设将积分区间[a,b]分为n等分,步长h=\dfrac{b-a}{n},选取等距节点x_k=a+kh 设将积分区间[a,b]分为n等分,步长h=nb−a,选取等距节点xk=a+kh 构造出的插值型求积公式 构造出的插值型求积公式 构造出的插值型求积公式
I n = ( b − a ) ∑ k = 0 n C k ( n ) f ( x k ) , I_n=(b-a)\sum_{k=0}^nC_k^{(n)}f(x_k), In=(b−a)k=0∑nCk(n)f(xk),
称为 牛顿-柯特斯 ( N e w t o w n − C o t e s ) 公式 , 式中 C k ( n ) 称为 柯特斯系数 . 称为\textbf{牛顿-柯特斯}(\mathrm{Newtown-Cotes})\textbf{公式},式中C_k^{(n)}称为\textbf{柯特斯系数}. 称为牛顿-柯特斯(Newtown−Cotes)公式,式中Ck(n)称为柯特斯系数.
根据求积系数 A k = ∫ a b l k ( x ) d x , k = 0 , 1 , … , n . 引进变换 x = a + t h , 则有 根据求积系数A_k=\int_a^bl_k(x)\mathrm{d}x,k=0,1,\ldots,n.引进变换x=a+th,则有 根据求积系数Ak=∫ablk(x)dx,k=0,1,…,n.引进变换x=a+th,则有
C k ( n ) = h b − a ∫ 0 n ∏ j = 0 j ≠ k n t − j k − j d t = ( − 1 ) n − k n k ! ( n − k ) ! ∫ 0 n ∏ j = 0 j ≠ k n ( t − j ) d t . C_k^{(n)}=\frac{h}{b-a}\int_0^n\prod_{j=0\\j\neq k}^n\frac{t-j}{k-j}\mathrm{d}t=\frac{(-1)^{n-k}}{nk!(n-k)!}\int_0^n\prod_{j=0\\j\neq k}^n(t-j)\mathrm{d}t. Ck(n)=b−ah∫0nj=0j=k∏nk−jt−jdt=nk!(n−k)!(−1)n−k∫0nj=0j=k∏n(t−j)dt.
特别地,当 n = 2 时 , 相应的求积公式称为 辛普森 ( S i m p s o n ) 公式 : 特别地,当n=2时,相应的求积公式称为\textbf{辛普森}(\mathrm{Simpson})\textbf{公式}: 特别地,当n=2时,相应的求积公式称为辛普森(Simpson)公式:
S = b − a 6 [ f ( a ) + 4 f ( a + b 2 ) + f ( b ) ] . S=\frac{b-a}{6}\left[f(a)+4f(\frac{a+b}{2})+f(b)\right]. S=6b−a[f(a)+4f(2a+b)+f(b)].
2.2 Python实现牛顿-柯特斯公式
def newtown_cotes_integrate(equal_segment, interval_start, interval_end, symbol_t, f_x):
"""
实现牛顿-柯特斯(Newton-Cotes)插值型积分
:param symbol_t: 引进变换x=a+t*h后的积分变量
:param equal_segment: 区间等分数n
:param interval_start: 区间左端点即起点
:param interval_end: 区间右端点即终点
:param f_x: 被积函数 intergrand
:return:牛顿-柯特斯(Newton-Cotes)插值积分
"""
step_h = (interval_end - interval_start) / equal_segment
f_k_array = np.array([f_x.subs(x, interval_start + k * step_h) for k in range(equal_segment + 1)])
return (interval_end - interval_start) * np.sum(cotes_coefficient(equal_segment, symbol_t) * f_k_array)
def cotes_coefficient(equal_segment, symbol_t):
"""
实现牛顿-柯特斯(Newton-Cotes)插值型求积公式的柯特斯系数
:param equal_segment: 区间等分数n,其中1<=n<=7,n>7的牛顿-柯特斯公式计算不稳定,不使用.
:param symbol_t: 引进变换x=a+t*h后的积分变量t
:return: 柯特斯系数数组
"""
if equal_segment not in range(1, 8):
raise ValueError("Cotes coefficient must be an integer between 1 and 7")
c_k_array = np.zeros(equal_segment + 1, dtype=np.float64)
for k in range(equal_segment + 1):
index = list(range(equal_segment + 1))
index.pop(k)
intergrand = np.prod(symbol_t - np.array(index))
integral = integrate(intergrand, (symbol_t, 0, equal_segment))
c_k_array[k] = (-1) ** (equal_segment - k) / (
equal_segment * factorial(k) * factorial(equal_segment - k)) * integral
return c_k_array
3.复合梯形公式
3.1 定义
将区间 [ a , b ] 划分为 n 等份 , 分点 x k = a + k h , h = b − a n , k = 0 , 1 , … , n , 将区间[a,b]划分为n等份,分点x_k=a+kh,h=\dfrac{b-a}{n},k=0,1,\ldots,n, 将区间[a,b]划分为n等份,分点xk=a+kh,h=nb−a,k=0,1,…,n, 在每个子区间 [ x k , x k + 1 ] ( k = 0 , 1 , … , n − 1 ) 上 在每个子区间[x_k,x_{k+1}](k=0,1,\ldots,n-1)上 在每个子区间[xk,xk+1](k=0,1,…,n−1)上
采用梯形公式 ∫ a b f ( x ) d x ≈ b − a 2 [ f ( a ) + f ( b ) ] , 则得 采用梯形公式\int_a^b\!f(x)\mathrm{d}x\approx\dfrac{b-a}{2}[f(a)+f(b)],则得 采用梯形公式∫abf(x)dx≈2b−a[f(a)+f(b)],则得
T n = h 2 ∑ k = 0 n − 1 [ f ( x k ) + f ( x k + 1 ) ] = h 2 [ f ( a ) + 2 ∑ k = 1 n − 1 f ( x k ) + f ( b ) ] , T_n=\frac{h}{2}\sum_{k=0}^{n-1}[f(x_k)+f(x_{k+1})]=\frac{h}{2}\left[f(a)+2\sum_{k=1}^{n-1}f(x_k)+f(b)\right], Tn=2hk=0∑n−1[f(xk)+f(xk+1)]=2h[f(a)+2k=1∑n−1f(xk)+f(b)],
称为复合梯形公式
3.2 Python实现复合梯形公式
def com_trapz(a, b, equal_segment, intergrand):
"""
实现复合梯形求积公式
:param a: 区间左端点即起点a
:param b: 区间右端点即终点b
:param equal_segment: 区间等分数n
:param intergrand: 被积函数f(x)
:return: 复合梯形求积积分
"""
step_h = (b - a) / equal_segment
f_x_k_array = np.array([intergrand.subs(x, a + k * step_h) for k in range(1, equal_segment)])
return step_h / 2 * (intergrand.subs(x, a) + 2 * np.sum(f_x_k_array) + intergrand.subs(x, b))
4.复合辛普森公式
4.1 定义
将区间 [ a , b ] 划分为 n 等份 , 在每个子区间 [ x k , x k + 1 ] ( k = 0 , 1 , … , n − 1 ) 上 将区间[a,b]划分为n等份,在每个子区间[x_k,x_{k+1}](k=0,1,\ldots,n-1)上 将区间[a,b]划分为n等份,在每个子区间[xk,xk+1](k=0,1,…,n−1)上
采用辛普森公式 , 若记 x k + 1 / 2 = x k + 1 2 h , 则得 采用辛普森公式,若记x_{k+1/2}=x_k+\frac{1}{2}h,则得 采用辛普森公式,若记xk+1/2=xk+21h,则得
S n = h 6 ∑ k = 0 n − 1 [ f ( x k ) + 4 f ( x k + 1 / 2 ) + f ( x k + 1 ) ] = h 6 [ f ( a ) + 4 ∑ k = 0 n − 1 f ( x k + 1 / 2 ) + 2 ∑ k = 1 n − 1 f ( x k ) + f ( b ) ] , \begin{aligned} S_n&=\frac{h}{6}\sum_{k=0}^{n-1}[f(x_k)+4f(x_{k+1/2})+f(x_{k+1})]\\ &=\frac{h}{6}\left[f(a)+4\sum_{k=0}^{n-1}f(x_{k+1/2})+2\sum_{k=1}^{n-1}f(x_k)+f(b)\right], \end{aligned} Sn=6hk=0∑n−1[f(xk)+4f(xk+1/2)+f(xk+1)]=6h[f(a)+4k=0∑n−1f(xk+1/2)+2k=1∑n−1f(xk)+f(b)],
称为复合辛普森公式
4.2 Python实现复合辛普森公式
def com_simpson(a, b, equal_segment, intergrand):
"""
实现复合辛普森求积公式
:param a: 区间左端点即起点a
:param b: 区间右端点即终点b
:param equal_segment: 区间等分数n
:param intergrand: 被积函数f(x)
:return: 复合辛普森求积积分
"""
step_h = (b - a) / equal_segment
f_x_k1_array = np.array([intergrand.subs(x, a + (k+0.5) * step_h) for k in range(equal_segment)],
dtype=np.float64)
f_x_k2_array = np.array([intergrand.subs(x, a + k * step_h) for k in range(1, equal_segment)],
dtype=np.float64)
return step_h / 6 * (
intergrand.subs(x, a) + 4 * np.sum(f_x_k1_array) + 2 * np.sum(f_x_k2_array) + intergrand.subs(x, b))
5.测试
if __name__ == '__main__':
# 辛普森公式及其余项表达式测试成功,来源详见来源详见李庆扬数值分析第5版P135,e.g.4
# 0.632333680003663
inter_grand = exp(-x)
print("辛普森公式积分为:{}".format(newtown_cotes_integrate(2, 0, 1, x, inter_grand)))
print("辛普森公式为:{}".format(quadrature_reminder(a=0, b=1, equal_segment=2, m=3, intergrand=exp(-x), a_k=cotes_coefficient(2, x))[0]))
# 复合梯形公式和复合辛普森公式测试成功,来源详见来源详见李庆扬数值分析第5版P135,e.g.2(1)
f_x = x / (4 + x ** 2)
print("复合梯形公式积分:{}".format(com_trapz(a=0, b=1, equal_segment=8, intergrand=f_x))) # 0.111402354529548
print("复合辛普森公式积分:{}".format(com_simpson(a=0, b=1, equal_segment=8, intergrand=f_x))) # 0.111571813252631