离散傅里叶级数DFS与离散傅立叶变换DFT及MATLAB实现

离散傅里叶级数：DFS
离散时间序列x(n)满足x(n)=x(n+rN)，称为离散周期序列，其中N为周期，x(n)为主值序列。
周期序列可用离散傅里叶级数表示成
n=0,1,…,N-1
其中，X ̃(k)是周期序列离散傅里叶级数第K次谐波分量的系数，也称为周期序列的频谱，可表示为
k=0,1,…,N-1
上面两式是周期序列的一对傅里叶级数变换对。
令 WN=e^(-j 2π/N)，以上两式可简写为：
例如，xn={…0,1,2,3,0,1,2,3,0…}，可见其基本周期为N=4，WN=e^(-jπ/2)= - j，
因此有

$$X\left(0\right)=\sum _0^3\tilde{x}(n)=\tilde{x}(0)+\tilde{x}(1)+\tilde{x}(2)+\tilde{x}(3)=6$$

$$X\left(1\right)=\sum _0^3\tilde{x}(n)(-j{)}^n=-2+2j$$

$$X\left(2\right)=\sum _0^3\tilde{x}(n)(-j{)}^{2n}=-2$$

$$X\left(3\right)=\sum _0^3\tilde{x}(n)(-j{)}^{3n}=-2-2j$$

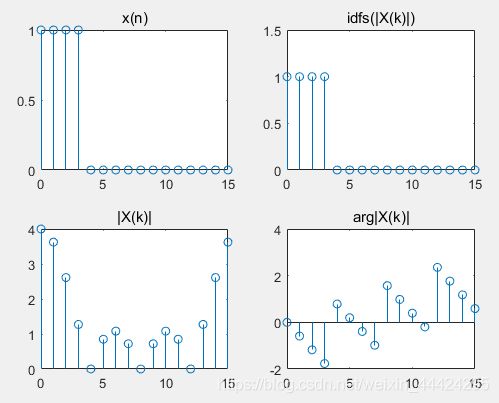
利用上述原理进行MATLAB编程，取一个周期性矩形序列的脉冲宽度占整个周期的1/4，一周期的采样点为16点。绘出用傅里叶级数求得的信号的幅度和相位频谱及傅里叶级数逆变换的图形如下：

function xk=dfs(xn,N)
       n=[0:1:N-1];        %n的行向量 
       k=n;               %k的行向量  
       WN=exp(-j*2*pi/N);  %WN因子
       nk=n'*k;            %产生一个含nk值的N乘N维矩阵
      WNnk=WN.^nk;       %DFS矩阵
      xk=xn* WNnk;        %DFS系数行向量

function xn=idfs(xk,N)
       n=[0:1:N-1];        %n的行向量 
       k=n;               %k的行向量  
       WN=exp(-j*2*pi/N);  %WN因子
      nk=n'*k;             %产生一个含nk值的N乘N维矩阵
      WNnk=WN.^(-nk);    %DFS矩阵
      xn=xk* WNnk/N;      %DFS系数行向量

N=16;
xn=[ones(1,N/4),zeros(1,3*N/4)];
n=0:N-1;
xk=dfs(xn,N);
xn1=idfs(xk,N);
subplot(2,2,1); stem(n,xn); title('x(n)');
subplot(2,2,2); stem(n,abs(xn1));  title('idfs(|X(k)|)');
subplot(2,2,3); stem(n,abs(xk));  title('|X(k)|');
subplot(2,2,4); stem(n,angle(xk));  title('arg|X(k)|');

离散傅里叶变换：DFT
对于非周期序列，在实际中常常使用有限长序列。x(n)是非周期序列，但可以理解为某一周期序列的主值序列。由离散傅立叶级数DFS和IDFS引出有限长序列的离散傅立叶正、逆变换关系式。如下：

DFT与DFS的关系
比较两者的变换对，可以看出两者的区别仅仅是将周期序列换成了有限长序列。
有限长序列x(n)可以看作是周期序列 的一个周期；反之周期序列 可以看作是有限长序列x(n)以N为周期的周期延拓。
由于公式非常相似，在程序编写上也基本一致。
已知周期序列的主值x(n)=[0,1,2,3,4,5]，对x(n)周期重复4次得xn1，利用MATLAB绘出其频谱图像观察DFT与DFS的关系如下：

xn=[0,1,2,3,4,5];   
N=length(xn);
n0=0:N-1;k0=0:N-1;
n=0:4*N-1;    k=0:4*N-1;
xn1=xn(mod(n,N)+1);
xk=xn*exp(-j*2*pi/N).^(n0'*k0);
xk1=xn1*exp(-j*2*pi/N).^(n'*k);
subplot(2,2,1);   stem(xn);            title('原主值信号x(n)');
subplot(2,2,2);   stem(n,xn1);         title('周期序列信号');
subplot(2,2,3);   stem(k0,abs(xk));     title('|X(k)|');
subplot(2,2,4);   stem(k,abs(xk1));   title('|X1(k)|');

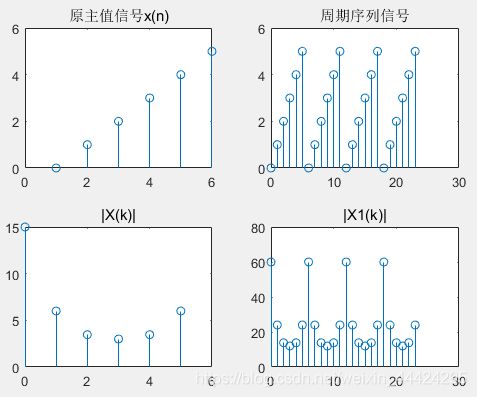
可见，有限长序列x(n)可以看成是周期序列的一个周期，反之，周期序列可以看成是有限长序列以N为周期的周期延拓。频域上的情况也是相同的。从这个意义上说，周期序列只是有限个序列值有意义。