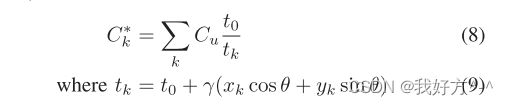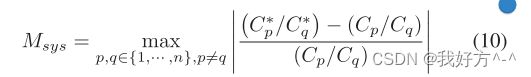有源和无源设备的共质心布局:回顾和未来之路
摘要
本文概述了在模拟设计中用于克服系统变化影响的共质心 (CC) 布局样式。 CC 布局必须仔细设计,以尽量减少失配的影响。 CC 版图的算法必须了解布线寄生效应、版图相关效应(对于有源器件)以及版图选择对性能的影响。 最佳 CC 布局还取决于诸如单元器件的选择以及不相关和系统变化的相对影响等因素。 本文还研究了非 CC 布局可能比 CC 布局更可取的场景。
本文对用于晶体管和无源器件的 CC 布局技术进行了调查。 尽管过去在构建 CC 布局方面进行了大量工作,但仍有许多工作要做。 构建低功耗解决方案的能力在很大程度上取决于开发构建具有低寄生效应的匹配良好的低电容结构的能力,而这仍然是一个悬而未决的问题。 早期的工作是了解 CC 布局何时优于非 CC 布局,反之亦然,但需要进一步研究。
新技术的出现——FinFET 和栅极环绕 FET(GAAFET/纳米带)——为 CC 布局带来了许多新挑战。 例如,在较低的金属层中,可能要求所有导线都在网格上,具有恒定的间距和宽度; 较低金属层中的所有导线必须是单向的; 从水平方向“转向”到垂直方向或反之亦然的成本会产生高过孔电阻。 此外,MOM 电容器比 MIM 结构更受青睐,因为从较低金属层移动到较高金属层的成本同样会在通孔堆叠上产生高电阻。 器件结构易受应力影响,需要放置假体以保持应力 [15]、[60]。
调研
在模拟/混合信号 (AMS) 电路中,工艺变化会导致电路性能参数的不可预测性。 AMS 电路的构建使其对器件或无源器件(难以控制)的过程引起的可变性的绝对值不太敏感,但仍对器件之间的差异可变性敏感(更易控制)。 例如,在运算跨导放大器 (OTA) 中的差分对 (DP) 等差分结构中,使用匹配可有效减少 OTA 性能的变化。 其他几种模拟结构,例如平面和 FinFET 技术中的有源器件(例如电流镜)和无源器件(例如电阻器/电容器阵列),需要匹配。 本文概述了共质心布局 [1],这是用于减少模拟布局中由工艺引起的差分失配的最广泛使用的技术之一。 公共质心 (CC) 技术为一组 k 个元素创建布局,每个设备 i 由 si 个单位组成。 CC 布局确保每个设备的单元的质心重合。
一般来说,CC 布局被认为比其他替代方案(例如叉指图案)更适合匹配工艺引起的变化,并且广泛用于匹配电路元件。 然而,应该注意的是,CC 布局可能涉及比其他替代方案更复杂的布线和更大的布线寄生效应。
本文概述了共质心布局 [1],这是用于减少模拟布局中由工艺引起的差分失配的最广泛使用的技术之一。 公共质心 (CC) 技术为一组 k 个元素创建布局,每个设备 i 由 si 个单位组成。 CC 布局确保每个设备的单元的质心重合。
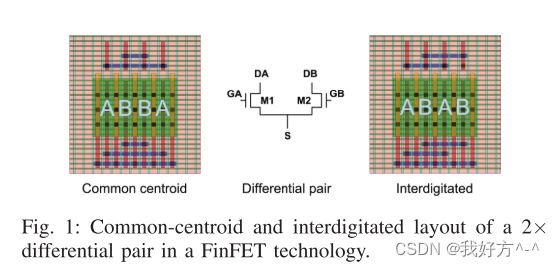
图 1 中 DP 的布局可以组织成两个元素的阵列,即设备 A 和 B(即 k = 2),每个元素由 sA = sB =2 个单位单元 [1] 组成。 CC 技术以 1D 或 2D 阵列布置设备,以便在阵列的每个维度中,质心匹配。 鉴于器件 j 的单元 i 的位置为 (xj i ,yj)对于如图 1 所示的一维布局,CC 标准为:
![]()
在图中,这是使用“ABBA”序列来满足的。 2D CC 布局图案围绕 X 轴和 Y 轴对称。 在一般的二维数组中,可类比得到。
相比之下,叉指布局交替放置 k 个器件中的每一个的指状物(或 FinFET 单位单元),例如,图 1 中显示的序列“ABAB”中的一维布局。叉指布局没有共同的质心 设备:在图中,A 细胞的质心位于 B 细胞的质心左侧。 一般来说,CC 布局被认为比其他替代方案(例如叉指图案)更适合匹配工艺引起的变化,并且广泛用于匹配电路元件。 然而,应该注意的是,CC 布局可能涉及比其他替代方案更复杂的布线和更大的布线寄生效应。
使用 CC 布局的基本原理是它们抵消了由于一阶工艺梯度引起的线性系统变化。 过程参数 p 的变化 Δp 会在电路性能参数 P 中引起小的扰动 ΔP。这可以使用线性泰勒级数展开来建模,其中 Sp = ∂P/∂p 是标称点的灵敏度。 使用质心作为原点,变化由平面 Δp = α · x 建模,其中 α 是变化的(可能未知的)梯度。 在水平维度 x 中,ΔP = αSp · x。对于线性变化,即常数 α,性能 P 是 x(每个设备的位置)的线性函数。
![]()
在这种线性假设下,CC 标准确保所有设备的变化之和相互抵消。 在图 1 中,假设 p 代表阈值电压,P 代表漏极电流。 由于 Δp = α · x,器件 A 的参数 p 相对于质心处的值移动了最左边的晶胞 -2α 和最右边的晶胞 +2α。 从方程式。 (5) 漏极电流偏移 -2αSp,A 和 +2αSp,A,净偏移加起来为零。 使用类似的符号,B 器件中的电流偏移电流偏移 -αSp,B 和 αSp,B,也产生零净偏移。 类似的论点证明 2D 布局中的 CC 是合理的。
一个类似的论点证明 2D 布局中的 CC 是合理的 此外,CC 布局的纵横比通常接近正方形 [2],其与原点的最大距离小于任何其他矩形,因此限制了系统变化的幅度 布局。
全局变化:这些同样影响芯片上的所有元件,不会导致模具上元件之间的不匹配,并使用工艺角很好地建模。
局部变化:这些包括基于梯度的系统变化和局部随机变化,它们可以使用空间相关模型 [3]-[5] 进行建模,从而在芯片上彼此更接近的元素具有较低的不匹配。 这些变化不会显着影响小型阵列 [6]-[8]。
- 工艺梯度建模
- 版图相关效应:在先进的技术节点中,版图相关效应 (LDE) [14]-[16] 会引起晶体管性能参数的变化。 这种转变取决于布局中要素的相对位置。 如图 2 所示,最常见的 LDE 包括:在纳米级 CMOS 节点中可以看到井邻近效应 (WPE),其中高能离子用于创建深逆行井剖面 [16]。 然而,高能离子会在光刻胶边缘散射并改变掺杂分布,从而改变器件的阈值电压 Vth 基于其与阱边缘的距离(如图 2(b)中的器件 B 所示)。 这种效应通常被称为 WPE [16],WPE 引起的失配可以通过使阱边缘远离器件或保持匹配器件的相等阱间距来最小化。扩散长度 (LOD) [17] 由于扩散区域长度的变化,会导致晶体管上的应力变化,从而导致其 Vth 变化。 LOD 的影响由两个参数 SA 和 SB 描述,即从多晶硅栅到器件两侧的扩散/有源边缘的距离。 对于栅极长度为 Lg 和 n 个单位单元的器件 [18]。氧化物定义 (OD) 间距和宽度 [14],也称为氧化物间距效应 (OSE),如图 2(b) 所示。 由于 OD 区(有源区)之间的间距变化,这种效应会改变晶体管中的应力,从而改变 Vth。 此外,在晶体管中产生的应力随 OD 宽度(有源区宽度)而变化。 通过保持相同的 OD 宽度和间距可以避免不匹配。栅极间距变化导致晶体管中感应的应力发生偏移 [14],如图 2(b) 中器件 A 所示。随着栅极间距增加,多晶硅周围的应力源材料的体积增加,导致应力增加 扰动 Vth 的晶体管通道。 在模拟单元中,通过使用相同的多晶硅间距,可以最大限度地减少失配。对匹配的设备使用相同的单位单元可用于抵消除 LOD 和 WPE 之外的所有 LDE [19]。 具体来说,CC 模拟块的栅极/多晶硅间距是统一的; 通过构造,单元格方法确保OD宽度是均匀的; 由于使用了基于行的单位单元放置方法,每个晶体管的 y 方向 OD 间距 (OSE) 是均匀的,并且由于扩散共享,x 方向的间距是均匀的。 因此,重点必须放在通过使用虚拟对象和使用放置技术来优化 LOD 和 WPE 不匹配上。
CC 电容器布局对于许多 AMS 集成电路中的电容器网络至关重要,例如电荷缩放数模转换器 (DAC)、逐次逼近寄存器模数转换器 (SAR ADC)、开关电容器滤波器和其他电路 需要电荷存储元件。 例如,CC 布局适用于图 4 中电荷缩放 DAC 中的二进制加权电容器网络,以实现高度匹配的电容比,同时减少不需要的寄生效应。 CC 电容器布局的质量取决于单元电容器结构、布局方式和单元电容器之间的布线。 变化的影响必须转化为电路性能指标,例如非线性和功耗。
电荷缩放数模转换器 [26]、[27] 的电容器网络中的寄生电容器 CTB、CTS、CBS,可能对整体电路性能和功耗有很大影响。
(DNL) 和积分非线性 (INL)。 DNL 量化了每个输出步距与理想步长的差异程度,可以通过方程式计算。 (22),而 INL 描述了 DAC 的理想输出和实际输出电平之间的最大偏差,可以通过公式计算。 (23)式中,VLSB是任意两个相邻数字码对应的理想输出电压差,称为最低有效位(LSB)。 如果 DAC 的 DNL 或 INL 差于 ±1 LSB,则可能导致非单调传递函数或丢失代码。 为了设计更强大的 DAC,DNL 和 INL 都被限制在 ±0.5 LSB 以内。
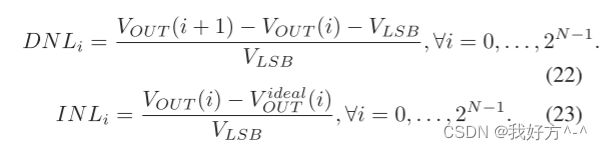
在这两个等式中,输出电压 VOUT 可能与理想值 Videal OUT (i) 相差甚远,如果没有匹配良好的 CC 布局。 功耗是另一个关键指标,因为许多 AMS 电路用于移动电池供电设备。 较大的单位电容器可以减少由于工艺变化和布线寄生引起的失配的影响,但可能会导致功耗和芯片面积显着增加。 因此,对于 CC 电容器布局,必须考虑在电容器失配和功耗之间进行更好的权衡。 林等人。 [26]、[27] 表明,最小化布线寄生不匹配可以导致所需的单位电容更小,从而降低功耗和面积。
建模 对片上变化进行建模
工艺引起的片上变化可以分为系统变化,可以预测的建模,或随机变化,只能用统计方法表示。 偏差也可以分为:
全局偏差:这些变化会类似地影响芯片上所有相似的元素,并且不会导致芯片上的元素之间的不匹配,并且使用工艺角进行了很好的建模。
局部变化:这些包括基于梯度的系统变化和局部随机变化,它们可以使用空间相关模型 [3]-[5] 进行建模,从而在芯片上彼此更接近的元素具有较低的不匹配。 这些变化不会显着影响小型阵列 [6]-[8]。
局部系统变化通常使用线性或非线性模型 [8] 表示,而随机变化使用分布建模。 局部随机变化可以通过它们的空间相关性来表征[5],[9]:不相关的变化甚至独立地影响相邻的元素,而空间相关的变化显示出一种相关趋势,该趋势随着元素之间的距离而衰减。 这可以通过称为相关距离 [10]、[11] 的度量来捕获(不相关变化的相关距离为零)。 工艺参数的总变化由下式给出:ΔP = g + u + s,其中 g、u 和 s 分别是全局、局部不相关和局部空间相关变化,方差为 σ2 g、σ2 u 和 σ2 s。 ΔP 的均值为零,其方差为σ2P = σ2g + σ2u + σ2s
系统偏差建模
工艺梯度 电容阵列
版图相关效应 晶体管
在先进的技术节点中,版图相关效应 (LDE) [14]-[16] 会引起晶体管性能参数的变化。 这种转变取决于布局中要素的相对位置。 如图 2 所示,最常见的 LDE 包括:
- 井邻近效应 (WPE):在纳米级 CMOS 节点中可以看到井邻近效应 (WPE),其中高能离子用于创建深逆行井剖面 [16]。 然而,高能离子在光刻胶边缘散射并改变掺杂分布,从而根据器件与阱边缘的距离修改器件的阈值电压 Vth(如图 2(b)中器件 B 所示)。 这种效应通常被称为 WPE [16],WPE 引起的失配可以通过使阱边缘远离器件或保持匹配器件的相等阱间距来最小化。
- 扩散长度 (LOD) [17] 由于扩散区域长度的变化,会导致晶体管上的应力变化,从而导致其 Vth 变化。 LOD 的影响由两个参数 SA 和 SB 描述,即从多晶硅栅到器件两侧的扩散/有源边缘的距离。 对于栅极长度为 Lg 和 n 个单位单元的器件 [18]:
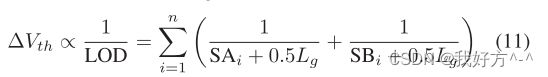
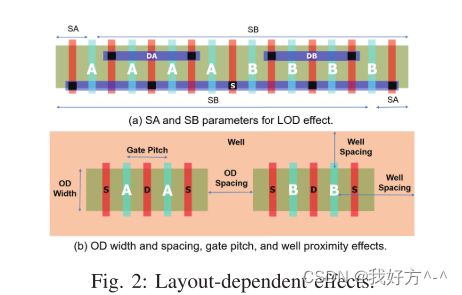 图 2(a) 说明了器件 A 和 B 的单位单元的 SA 和 SB。匹配的器件必须具有相同的 SA 和 SB 值,以匹配它们的阈值电压偏移 ΔVth。
图 2(a) 说明了器件 A 和 B 的单位单元的 SA 和 SB。匹配的器件必须具有相同的 SA 和 SB 值,以匹配它们的阈值电压偏移 ΔVth。 - 氧化物间距效应 (OSE) 氧化物定义 (OD) 间距和宽度 [14],也称为氧化物间距效应 (OSE),如图 2(b) 所示。 由于 OD 区(有源区)之间的间距变化,这种效应会改变晶体管中的应力,从而改变 Vth。 此外,在晶体管中产生的应力随 OD 宽度(有源区宽度)而变化。 通过保持相同的 OD 宽度和间距可以避免不匹配。
- 栅极间距变化导致晶体管中感应的应力发生偏移 [14],如图 2(b) 中器件 A 所示。随着栅极间距的增加,多晶硅周围的应力源材料的体积增加,导致应力增加 扰动 Vth 的晶体管通道。 在模拟单元中,通过使用相同的多晶硅间距,可以最大限度地减少失配。
对匹配的设备使用相同的单位单元可用于抵消除 LOD 和 WPE 之外的所有 LDE [19]。 具体来说,CC 模拟块的栅极/多晶硅间距是统一的; 通过构造,单元格方法确保OD宽度是均匀的; 由于使用了基于行的单位单元放置方法,每个晶体管的 y 方向 OD 间距 (OSE) 是均匀的,并且由于扩散共享,x 方向的间距是均匀的。 因此,重点必须放在通过使用虚拟对象和使用放置技术来优化 LOD 和 WPE 不匹配上。
相关性偏差
相关性模型
无源 整体相关性模型
对于有源设备,[10]、[11] 的空间相关模型使用相距 r 的两个设备之间的以下相关函数对设备变化进行建模:

随机偏差建模
由于随机掺杂剂波动 (RDF) [21] 或线边缘粗糙度 (LER) [22] 导致的不相关随机变化可以通过使用更大的器件来减少。 Pelgrom [23] 提出了模拟设计中使用最广泛的晶体管变分模型之一。 该模型将两个设备的参数 P(例如 Vth)中的不匹配量化为对应于不相关分量 u 和空间相关分量 s 的两个随机变量的总和。 失配的方差由下式给出
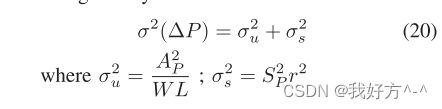
其中,AP 和 SP 是与技术相关的比例常数,r 是设备之间的距离,σ2 表示相应随机变量的方差。 第一个组件取决于晶体管的面积,可以通过使用大尺寸晶体管来稀释,而第二个组件取决于组件之间的距离,并且可以通过减少器件之间距离的布局来减轻。 电容器 [24]、[25] 的类似模型使用
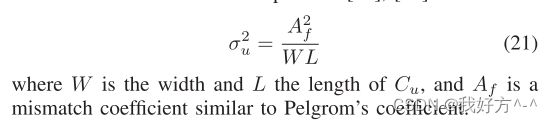
电容结构
| 电容类型 | 结构 | 优缺点 | 引用 |
|---|---|---|---|
| MOM | 手指 | - | [24,29,30] |
| MOM | 三明治 | - | [31] |
| MOM | 柱子 | - | [32-34] |
| MIM | 榫 | - | [35] |
| MIM | 竖条 | - | [36] |
与 MIM 电容器相比,MOM 电容器具有制造成本更低以及由于先进工艺节点中金属层数和金属宽度/间距缩小而具有更高电容密度的优势。
指状结构最容易实现,电容密度最高。 指状结构对 FinFET 技术友好,因为较低的金属层必须以恒定的宽度和间距进行网格化。 然而,在非 FinFET 节点中,它们可能会在布线后产生各种不需要的寄生效应,如图 4 所示,从而导致意外的增益损失或更高的开关能量。 顶板和基板之间的大寄生电容 C T S C^{TS} CTS 可能会导致显着的增益损失 [30]。 除 CTS 外,由于手指与连接不同电容器的金属线之间的耦合,手指结构的布线还可能在 SAR ADC 中不同电容器的顶板和底板之间产生较大的寄生电容 C T B C^{TB} CTB。 【着重考虑解决这个问题】
夹层结构、柱状结构、榫卯结构可以有效减少一些不需要的寄生,使布线更容易。 例如,这些结构中的 CTS 被消除,因为顶板金属形状被底板金属形状包围。 但是,这三种结构都比较复杂,对应的电容密度没有指状结构那么高。 [28] 中引入了考虑各种尺寸和层的参数化榫卯结构,用于快速生成单位电容器,同时实现各种单位电容值的高电容密度。
电容阵列CC
| 分类 | 引用编号 | 优缺点 |
|---|---|---|
| 启发式 | [12,20,37] | [12] 中,使用矩形和圆的概念来开发布局和路由算法。 [20] 的工作表明,两个电容器之间的高色散度可以保证更高的相关系数和更低的变异。在文献 [37] 中,提出了一种启发式非CC布局算法来增加电容器之间的相关性,以牺牲系统变化为代价来改进相关随机变化。 |
| 整数线性规划 | [38] | 约束包括排他性,在每个位置只插入一个单元电容;比率要求,确保单元电容器的数量应该完全等于所需的数量;以及一个路由约束,即每个单元电容器在其四个相邻通道中唯一地选择一个轨道进行路由,其中每个轨道跨越电容器之间的整个通道。 |
| 结构化方法 | [39-44] | 基于 [39] 中提出并在 [40]、[41] 中开发的棋盘布局样式。 该方法侧重于二进制加权电容比。[42] 提出了一种考虑寄生影响的基于分区中心的对称放置算法。 在 [43] 中,棋盘放置方法被推广到基于混合棋盘放置方法的非二进制电容比,该方法旨在获得最低的 DNL,同时将布线长度与电容比值精确匹配。 棋盘布线涉及许多过孔,由于过孔电阻高,可能导致 3dB 频率下降,尤其是在 FinFET 节点中。 在 [44] 中,提出了使用块棋盘方法改进 3dB 频率,该方法将电容器以各种粒度放置在棋盘图案中。 |
| 基于随机优化算法的迭代技术 | [13,45,46,27] | [13] 的工作提出了一个共同的质心放置,以最大化分散,同时尊重非整数电容器比率的邻接约束,以同时减少系统和随机失配。 来自对序列的一对单位电容器相对于放置矩阵的CC点对称放置,从最内圈开始向外方向。 [13] 的工作在对序列的扰动期间提出了三个操作以增加分散程度,并设计了一个程序来保持可行的放置,从而在每次扰动后满足邻接约束。 但是,布局并没有考虑布线复杂性。在 [45] 中提出了一种基于中心角块列表 (C-CBL) 的放置方法,用于 CC 放置,使用基于网格的方法均匀放置器件,以便它们可以平均寄生效应。 在通过改变列数和消除冗余解决方案生成几个可行的位置之后,SA 用于扰动全局序列对,他们重新定义了移动以扰动子设备的位置。 但是,没有考虑路由注意事项。[46] 中基于 SA 的 CC 布局生成方法执行同时布局和全局布线,对 CC 布局的一对序列表示执行搜索。 在每一对 (ui,uj) 中,ui 和 uj 关于 CC 点对称放置,并且 pair 序列以距 CC 点的距离不递增的顺序列出对。 对序列的扰动可能导致具有相同尺寸的不同 CC 布局。 [46] 中的一个核心步骤是可布线性分析,它发现不同连接电容器组之间的重叠通道跨度。 接下来,最小化通道中所需的最大数量的路由轨道,尝试实现每个通道一个轨道。 最后,详细布线(图 7)首先在通道中布线主干线,然后使用广度优先搜索在阵列内布线分支线,最后是对称连接所有主干线的桥接线。在 [27] 中,提出了一种构建最小生成树 (MST) 以连接所有不相交连接组件的顶板的方法。 该方法定义了对单位电容器尺寸、布线拓扑和布线模式进行编码的 CP 序列。 采用遗传算法来找到 CP 序列的最佳配置,用于功率最小化和寄生匹配【在分散电容器的布局方面走极端,导致高寄生开销和布线复杂性。C15-1】 |
晶体管CC
电容器阵列的 CC 布局算法并不直接适用于晶体管阵列,其中必须考虑扩散共享和 LDE 等因素。 在 [2]、[47]-[51] 中研究了 CC 布局以最小化晶体管阵列的系统变化。
| 分类 | 引用编号 | 优缺点 |
|---|---|---|
| 构造算法 | [47,48,48] | [48]、[49] 中的工作提出了构造算法来生成晶体管阵列的 CC 模式。 在 [49] 中,热效应也被考虑用于布局生成。 在 [47] 中,分散的概念,即晶体管的单位单元在整个布局中分布的程度,用于比较布局和生成最大分散布局的方法。 然而,所提出的技术只能应用于具有两个晶体管的阵列。 这些方法都没有解决路由问题,或者晶体管之间的扩散共享问题。 |
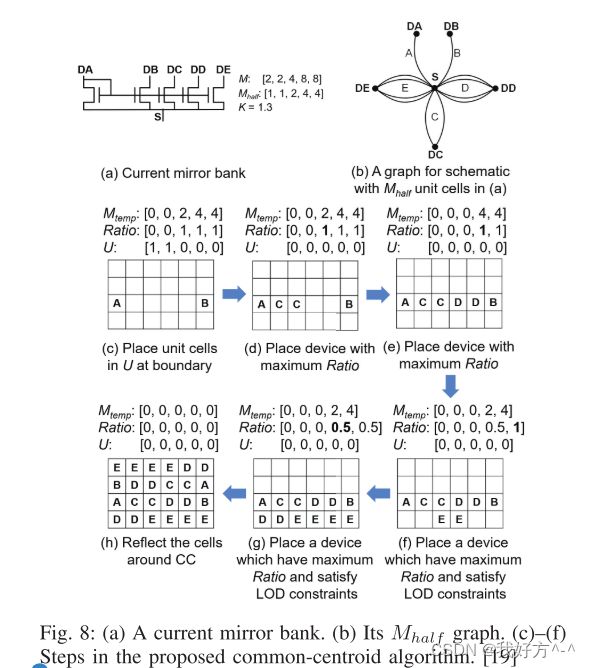
| [2] | 2D CC 阵列以最大化扩散共享的框架,将节点表示为顶点和晶体管指之间的源漏连接作为边,首先通过将顶点之间的边数减半来创建“半扩散图”Mhalf。 图 8(a) 显示了由五个器件 A、B、C、D 和 E 组成的示例电路的示意图,其多重矩阵 M = [2, 2, 4, 8, 8] 表示,在同一个 顺序,这五个设备的单元格数。 电路图如图 8(b) 所示。 [19] 中的扩展认为单位单元的数量是奇数,完全扩散共享是不可能的。 在这种情况下,一个单元格被放置在布局的边缘。 然后在该图上找到欧拉路径(在 [2] 中,这是通过昂贵的枚举完成的)以创建一半的布局:然后将其反映在 CC 点上以创建完整的布局。 | |
| [19] | [19] 中的工作,并入 ALIGN [52]-[54],引入了对先前方法的一些改进。 首先,它改进了 [2] 中昂贵的欧拉路径枚举。 其次,它解释了构建 CC 布局时的 LDE 和寄生不匹配。 第三,通过创建优化线宽的鱼骨结构,使布线方法具有电迁移感知和 IR 压降感知。 该方法如图 8©-(f) 所示。 在每个步骤中,将具有最大比例(比率)未放置单元的器件单元添加到布局矩阵中。 为了改善分散,单元格交替放置在 CC 点的左侧和右侧。 如果设备已被放置在列中(在不同的行中),为了最大限度地减少 LOD 不匹配,另一个设备被优先考虑。 | |
| [50] | 在 [50] 中,研究了考虑栅极错位影响的 FinFET 技术的 CC 布局。 由于栅极未对准,FinFET 的印刷栅极位置可能会偏离预期位置,从而增加阈值电压并降低 FinFET 漏极电流。 通过仔细安排电流镜或差分对内所有 FinFET 的方向,可以完美匹配电流镜或差分对中不同晶体管之间的漏极电流比 [55]。 提出了一种新的质量指标,用于评估电流镜中晶体管之间的电流比匹配,这些晶体管在栅极未对准和 CC 阵列中的寄生电阻下。 专注于电流镜结构的布局算法具有扩散共享意识,并最大限度地提高晶胞色散,以优化电流比,同时最大限度地提高色散度。 使用基于最小生成树方法的寄生感知技术执行路由。 |
数据集
实验指标
电容,晶体管,FinFET是晶体管的一种类型。MOM电容也有finger
总结
- 有源空间相关性模型[10][11]
- 随机掺杂剂波动 (RDF) [21] 或线边缘粗糙度 (LER) [22]
Nibedita Karmokar, Meghna Madhusudan, Arvind K. Sharma, Ramesh Harjani, Mark Po-Hung Lin, Sachin S. Sapatnekar, “Common-Centroid Layout for Active and Passive Devices: A Review and the Road Ahead”, 2022 27th Asia and South Pacific Design Automation Conference (ASP-DAC), pp.114-121, 2022.