2022年认证杯SPSSPRO杯数学建模C题(第二阶段)污水流行病学原理在新冠疫情防控方面的作用求解全过程文档及程序

2022年认证杯SPSSPRO杯数学建模

C题 污水流行病学原理在新冠疫情防控方面的作用

原题再现：

  2019 年新型冠状病毒肺炎疫情暴发至今已过两年，新型冠状病毒历经多次变异，目前已有 11 种变异毒株，包括阿尔法、贝塔、德尔塔、奥密克戎等。其中变异株奥密克戎已在世界上多个国家和地区流行。相比此前流行的变异株，奥密克戎具有大量关键突变，其传播力和隐匿性更强，且存在免疫逃逸，更容易多点散发或集中暴发。截至 2021-12-08，全球共有 57 个国家和地区报告奥密克戎变异株，截至 2022-01-20，奥密克戎已经波及我国 14 个省。虽然可以通过区域全员核酸检测的方式快速发现感染者并进行有效隔离。但是大规模核酸检测成本较高，而且对于经济、生活都会产生较大的影响，使用频率有限。为了解决这个问题，2020 年 8 月，世界卫生组织（WHO）发布了名为“新冠病毒环境监测的现状（Status of environmental surveillance forSARS-CoV-2 virus）”的科学简报。文中总结了通过市政污水进行新冠病毒监测的背景、方法和用途，为全球抗击疫情提供了一份指导方案。污水监测是以污水流行病学（Wastewater-Based Epidemiology，WBE）的原理为手段，通过分析市政污水处理厂进水中的污染物或者生物标记物浓度，结合人体代谢机理、进水流量和服务人群数量等信息，反推该物质在污水集水区内的状况，这一方法或在未来新冠疫情的大规模防控上发挥重要的作用。
  所谓污水流行病学便是基于污水中蕴藏的丰富信息，通过分析污水处理厂进水中的化学物质浓度，根据人体代谢机理、进水流量和服务人口数量估算该地区人群消费某类化学物质的规律，调查与之相关的疾病、消费、健康等公众信息，从而预防和控制相关疾病，提高公众健康水平的科学。当前正在全球范围内流行的新冠疫情，更是将污水流行病学的应用扩展到对疫情的定性早期预警、对疾病流行率的定量估计以及疾病突发的定量警报，进一步拓展了污水流行病学的内涵。该方法有如下几个优点：1、监测的范围大、覆盖面广，可以评估大规模的社区总体的感染情况。市政污水厂通过污水管网承接了城市千家万户排放的污水，污水集水区域的人口数量少则千人，多则上百万人，覆盖的人口非常广泛，包括不能及时或者未发现症状而不进行核酸检测的感染者，因此能够更好的对疫情进行评估和预测。2、可预知病毒社区感染的重新爆发。由于污水新冠病毒的检测结果比临床患者出现早，因此会有预警作用。3、可作为疾病传播动态监测的辅助手段。对卫生监督结果进行有效的补充，这一点在中低收入的国家尤为重要。
  第二阶段问题：
  1. 污水流行病学（WBE）方法用于新冠疫情估计的的主要挑战之一是有很多变量的取值存在不确定性，这些不确定性主要源于样品采集、物质稳定性、人口数量估算、物质的人体代谢比例、物质的浓度测定、污水厂进水流量等方面。校正因子（CF）是将污水中测定的生物标记物质量转化为人群最终消费量的一个重要参数，CF 被认为是一个不确定性的来源，对最终消费量估计的准确性有显著影响。然而，大多数 CF 的估计值来源于一些旧的药代动力学研究，这里需要你们的团队根据数据，建立合理的模型对 CF 进行重新的估计和改进，以提高 WBE 方法的准确性。
  2. 请选取美国的几个主要城市中心（总人口相当于 300 万以上）进行研究，通过对污水中 SARS-CoV-2 RNA 的流行率进行纵向分析来评估该地区的疫情防控措施的主要作用，并给出合理化建议。

整体求解过程概述(摘要)

  突发的新型冠状病毒肺炎（COVID-19）已蔓延至全球几乎所有的国家，累计确诊病例已超过 1 亿例。污水中含有大量基于人类消费的药物，校正因子（CF）是将污水中测定的生物标记物质量转化为人群最终消费量的一个重要参数，对最终消费量估计的准确性有显著影响。然而，大多数 CF 的估计值来源于一些旧的药代动力学研究，该方法过程复杂、可实施性不强、成本高。基于此，本文主要针对污水监测数据和搜集到的美国疫情相关数据建立 Rayleigh 模型、多元回归模型、随机森林、BP 神经网络和 DEA 综合效率评价模型，估计 CF 并研究污水监测在新冠疫情防控方面的应用。
  针对问题一，要求建立合理的模型对 CF 进行重新的估计和改进，以提高WBE 方 法 的 准 确 性 。 基 于 此 问 题 ， 本 文 主 要 利 用 污 水 中 监 测 到 的SARS-CoV-2 RNA 浓度（cvl）、15 天内变化浓度（pc）分别对污水采样样本中监测出含有病毒的样本比例（pws）建立 Rayleigh 模型，利用该模型推算出校正方 程 ， 并 在 线 性 和 平 方 检 测 器 下 分 别 估 计 出 校 正 因 子 CF ， 然 后 利 用Monte Carlo 仿真模拟证明该方法的有效性，最后根据估计出的校正因子，合理的推断人体消费量，从而达到对新冠病毒的一个预警。结果显示：在线性监测器下，常数校正因子 A1=1.464243，斜率校正因子 B1=7.930901，由此可推出，在1 单位的 SARS-CoV-2 RNA 病毒浓度下，可推算出 B1+A1 单位的真实病毒浓度存在于当地。同样，在平方检测器下，1 单位的 7 天平均 SARS-CoV-2 RNA 病毒变化浓度下，有 B2+A2 单位的病毒浓度变化量。
  针对问题二，要求选取美国的几个主要城市中心（总人口相当于 300 万以上）进行研究，通过对污水中 SARS-CoV-2 RNA 的流行率进行纵向分析来评估该地区的疫情防控措施的主要作用，并给出合理化建议。基于此问题，本文主要针对搜集到的数据建立随机森林、BP 神经网络分析了在本次疫情中各种因素对美国新增新冠病例的重要影响作用；选取人口数高于 300 万的纽约和洛杉矶各个指标数据建立 DEA 综合效率评价模型，综合分析了污水中 SARS-CoV-2 RNA 的流行率与其他因素间的关系，并评估该地区的疫情防控措施的主要作用。
  最后，本文研究了所建立的模型优缺点、综合分析了研究结果，给当地政府提供了了对疫情防控的预判信息，并给出一定的防控建议。

问题分析：

  大多数 CF（校正因子） 的估计值来源于一些旧的药代动力学研究，药物代谢动力学（Pharmacokinetic）是定量研究药物在生物体内吸收、分布、代谢和排泄规律，并运用数学原理和方法阐述血药浓度随时间变化的规律的一门学科。其过程复杂、可实施性不强、成本高。在此背景下，本文主要利用污水中监测到的SARS-CoV-2 RNA 浓度（cvl）、15 天内变化浓度（pc）分别对污水采样样本中监测出含有病毒的样本比例（pws）建立 Rayleigh 模型，利用该模型推算出校正方程，并在线性和平方检测器下分别估计出校正因子 CF，然后利用 Monte Carlo仿真模拟证明该方法的有效性，最后根据估计出的校正因子，合理的推断人体消费量，从而达到对新冠病毒的一个预警。
  针对问题二，本文首先根据搜集到的美国疫情相关数据建立随机森林、BP神经网络分析各种因素对美国新增新冠病例的影响作用。为研究各城市疫情防控措施的作用，本文对问题一中的指标进行“再提取”，加上新增的综合反映该城市医疗资源的利用效率和该城市 SARS-CoV-2 RNA 的流行率、医疗资源分配有效性以及防控能力的投入指标：污水病毒监测点服务人口数、该城市施用疫苗剂量和疫苗有效性数据等，产出指标：该城市疫苗接种覆盖率、该城市医院住院率等，最后根据提取的指标和题目要求美国总人口大于300 万的主要城市数据建立 DEA-BCC 模型和 DEA-CCR 模型进行研究分析，计算出该城市医疗设备和资源的利用率，研究该城市医疗设备和资源投入与产出是否存在冗余和不足的现象。最后根据所计算的结果给出合理的疫情防控建议。

模型假设：

  （1）假设搜集整理的数据真实可靠，与实际相符。
  （2）假设人群产生的代谢产物全部通过下水道，不存在其他方式排放生活污水。
  （3）假设污水中的病毒 SARS-CoV-2 RNA 主要来源于人类的消费，与其他次要来源无关。
  （4）假设数据预处理过程中无有效数据的丢失。

模型的建立与求解

  污水流行病学（WBE）方法用于新冠疫情估计的的主要挑战之一是有很多变量的取值存在不确定性，这些不确定性主要源于样品采集、物质稳定性、人口数量估算、物质的人体代谢比例、物质的浓度测定、污水厂进水流量等方面。校正因子（CF）是将污水中测定的生物标记物质量转化为人群最终消费量的一个重要参数，CF 被认为是一个不确定性的来源，对最终消费量估计的准确性有显著影响。
  然而，大多数 CF 的估计值来源于一些旧的药代动力学研究，药物代谢动力学（Pharmacokinetic）是定量研究药物在生物体内吸收、分布、代谢和排泄规律，并运用数学原理和方法阐述血药浓度随时间变化的规律的一门学科。其过程复杂、可实施性不强、成本高。下面本文将利用新的估计方法对 CF 进行估计，并利用Monte Carlo 仿真模拟证明该方法的有效性。

校正因子（CF）估计公式推导

基于 Rayleigh 模型的校正因子估计

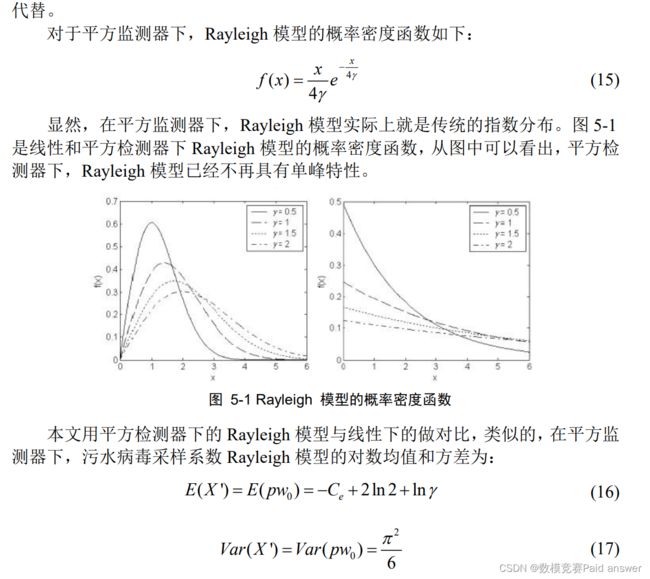
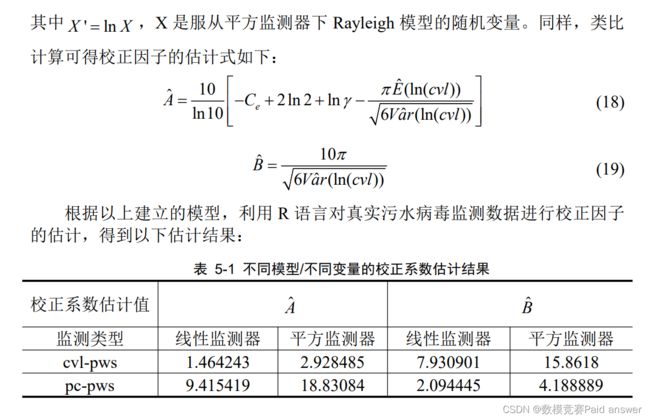
  污水流行病学（WBE）方法用于新冠疫情估计的的主要挑战之一是有很多变量的取值存在不确定性，这些不确定性主要源于样品采集、物质稳定性、人口数量估算、物质的人体代谢比例、物质的浓度测定、污水厂进水流量等方面，正是因为这些变量存在着不确定性，导致了在测量污水中的病毒含量并推算人体消费量时存在着很大的偏差。解决此类偏差的一个有效的方法是使用校正方程对变量进行校正，而校正方程的关键在于合理的估计出校正因子[4]。
  本文就官网提供的污水检测数据，利用污水测量病毒浓度与测量病毒样本占比建立 Rayleigh 模型，利用该模型推算出校正方程[5]，只需要知道病毒在污水中的测量浓度和测量病毒样本占比，就能合理的推算估计出校正因子具体的值。如上表所示，在线性监测器下，常数校正因子 A1=1.464243，斜率校正因子B1=7.930901，由此可推出，在 1 单位的 SARS-CoV-2 RNA 病毒浓度下，可推算出 B1+A1 单位的人体消费量。同样，在平方检测器下，1 单位的 7 天平均SARS-CoV-2 RNA 病毒变化浓度下，有 B2+A2 单位的人体消费量。

Monte Carlo 仿真模拟

  Monte Carlo 仿真[6]的一个重要问题就是如何产生服从特定分布的样本。本文使用 Rayleigh 模型描述病毒浓度，产生服从 Rayleigh 模型的样本，然后获得 cvl的样本值。对于一组 cvl 的样本值，使用 5.1.1 节提出的方法估计出校正因子，这就完成了一次仿真实验。由于样本产生的随机性，往往需要独立运行多次仿真实验，并把多次仿真实验结果的均值和标准差作为最终估计的结果，这就是Monte-Carlo 仿真[7]的一般步骤。总值，基于病毒浓度的 Rayleigh 模型的校正因子估计的软件编程实现方法可以归纳为以下五步：
  （1）产生服从 Rayleigh 模型的样本;
  （2）生成 cvl 的样本值;
  （3）根据公式（7）（8）计算 cvl 的对数的样本均值和样本方差;
  （4）根据公式（18）（19），获得校正因子的一次估计值;
  （5）重复 Monte-Carlo 仿真，计算多次估计值的平均值和标准差，获得校正因子的最终估计结果。
  为了精确评价所提方法的估计性能[8]，本文采用仿真数据进行实验，即先仿真产生服从 Rayleigh 模型的样本，然后再生成 cvl 的样本值。为了克服样本产生随机性的这一缺陷，采用 Monte-Carlo 模拟的方法，即使用多次仿真结果的平均值作为最终的估计值。校正因子估计首先要计算 cvl 样本对数的均值和方差的估计值，因此，样本数量是影响校正因子估计性能的重要因素。



  我们在网站上找到新增死亡人数、新增病例、入院人数、未参保认识、疫苗接种量等变量，我们以新增病例为 SARS-CoV-2 RNA 流行率指标进行建模，研究影响流行率的一些主要的因素。以新增病例为因变量，其余变量为自变量，如下所示：

  然后，我们选用了回归分析、BP 神经网络、随机森林三种方法，通过对这三种方法进行比较，选择拟合效果最好的模型，对影响 SARS-CoV-2 RNA 流行率的各个因素进行分析。

  如表 6-2 所示，我们可以看到随机森林的拟合效果比较好，其 R^2 为 0.832224，且明显高于神经网络和随机森林算法，所以我们选择用随机森林对流行率进行分析。下面我们对影响流行率的七个因素进行分析，得到各个因素对合格率的影响程度，结果如下所示：

  从表 6-3 中可以看出对流行率影响最大的是社会脆弱性指数，其权重值达到了 0.437402，七天平均新增以及未参保人数对流行率也有着很大的影响，其重要性权重为 0.212474 和 0.191110，疫苗接种情况也对流行率有着明显的影响，至于住院人数和死亡病例对流行率的影响很小。

  从图 6-3 中可以看到，社会脆弱性指数对流行率的影响最大，其标准差的波动也比较大，表明社会脆弱性指数对流行率的影响波动也比较大，七天平均新增、未参保人数对流行率也有着显著的影响，其标准差也非常大，表明其对流行率的影响的波动也比较大。完全接种疫苗数虽然对流行率没有太大的影响，但是其标准差较大，表明其对流行率影响的波动也会去较大，同样，住院人数和死亡病例对流行率的影响很小。

基于随机森林模型的结论与建议

  （1）从模型结果我们可以看到，社会脆弱指数对病毒的影响非常的大，针对新冠肺炎的流行，首先应该从社会角度出发，创造一个好的社会秩序，创建一个能够抵御病毒的社会环境，会大大降低病毒的传播，能够对国家消除病毒产生极大的帮助。
  （2）根据随机森林模型我们可以得出结论，未参保的人数也对病毒的传播有着显著的影响，参保可以降低病毒带来的意外伤害，使人们的生活水平不会很大程度的受影响，以至于生活困难，所以说提升人们的生活水平，加强人们的参保意识，能够使人们有低于病毒的意识，从而可以降低病毒的流行率。
  （3）疫苗的接种情况对病毒的流行率也有着很大程度的影响，政府方面应该加大医疗资源的投入，使疫苗免费普及，全面的组织人们进行疫苗的接种，从而去阻止病毒的流行，降低病毒的流行率。

论文缩略图：

程序代码：

问题一程序

data.wushui <- read.delim("clipboard")
names(data.wushui) <- c("Sewershed ID","Reporting Jurisdiction","County","Populat
ion Served", "Current virus levels","Percent change ","Percent of wastewater samples ")
cvl <-data.wushui[,6]
pws <-data.wushui[,8]
cvl[which(cvl==0)] <- 0.01
pws[which(pws==0)] <- 0.01
l_cvl<- log(cvl)
l_pws<- log(pws)
ce <- 0.5772
lamda <- exp(2*(mean(l_pws)+ce/2-log(2)))
a <- 10/log(10)
A.hat <- a*(-ce+2*log(2)+log(lamda)-pi*mean(l_cvl)/sqrt(6*var(l_cvl)))
B.hat <- 10*pi/sqrt(6*var(l_cvl))
A.hat0 <- a*(-ce/2+log(2)+log(lamda)/2-pi*mean(l_cvl)/sqrt(24*var(l_cvl)))
B.hat0 <- 10*pi/sqrt(24*var(l_cvl))
pc <- data.wushui[,7]
which.min(pc)
pc[64]
pc <- pc+100
pc[which(pc==0)] <- 0.01
l_pc <- log(pc)
A.hat1 <- a*(-ce+2*log(2)+log(lamda)-pi*mean(l_pc )/sqrt(6*var(l_pc )))
B.hat1 <- 10*pi/sqrt(6*var(l_pc ))
A.hat10 <- a*(-ce/2+log(2)+log(lamda)/2-pi*mean(l_pc)/sqrt(24*var(l_pc)))
B.hat10 <- 10*pi/sqrt(24*var(l_pc))
#MCMC 模拟
library(dplyr)
library(tidyverse)
library(ggplot2)#
data.mcmc<- read.delim("clipboard")
attach(data.mcmc)
x11()
plot(校正因子 A 的估计值~运行次数,data =data.mcmc,type = "l",col="red")
abline(h = 10)
legend(80, 12.8, c("真实值", "估计值"), col = c("black","red"), text.col = "green4", lty = c(1,1), merge = TRUE, bg = "gray90")
names(data.mcmc) <- c("运行次数","校正因子 A 的估计值","校正因子 B 的估计值
")
plot(校正因子 B 的估计值~运行次数,data =data.mcmc,type = "l",col="blue")
abline(h = 12)
legend(80, 15.5, c("真实值", "估计值"), col = c("black","blue"), text.col = "green4", lty = c(1,1), merge = TRUE, bg = "gray90")

问题二程序

import numpy as np
import scipy
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV
from sklearn.metrics import roc_curve, auc, roc_auc_score
import matplotlib.pyplot as plt
df=pd.read_csv('C:\\Users\\86187\\Desktop\\.csv')
df.head()
df.nunique()
y=df.y
y.head()
x=df.drop('y', axis=1) #dataframe.drop('isrun', axis=1)
x=x.drop('Date', axis=1)
x.head()
xtrain, xtest, ytrain, ytest = train_test_split(x, y, test_size=0.3, random_state=seed)
rfc = RandomForestRegressor() #实例化
rfc = rfc.fit(xtrain,ytrain) #用训练集数据训练模型
result = rfc.score(xtest,ytest)
result
model = MLPRegressor(hidden_layer_sizes=(2,2), activation='relu', solver='adam', alpha=0.0001, batch_size='auto&apos
learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=5000, shuffle=True
early_stopping=False,beta_1=0.9, beta_2=0.999, epsilon=1e-08
)
model.fit(X,Y)
display("神经网络 R2：%f"%(r2_score(Y,model.predict(X))))
model = LinearRegression()
model.fit(X,Y)
display("线性回归 R2：%f"%(r2_score(Y,model.predict(X))))
model = DecisionTreeRegressor()
model.fit(X,Y)
display("决策树 R2：%f"%(r2_score(Y,model.predict(X))))
modelY = RandomForestRegressor()
modelY.fit(X,Y)
display("随机森林 R2：%f"%(r2_score(Y,model.predict(X))))
XGBmodelY = xgb.XGBRegressor()
XGBmodelY.fit(X,Y)
display("XGBoost R2：%f"%(r2_score(Y,XGBmodelY.predict(X))))
model = GradientBoostingRegressor()
model.fit(X,Y)
print ('所有的树:%s' % rfc.estimators_)
print ('判定结果：%s' % rfc.predict(xtest))
#print rfc.predict_proba(feature_test[0])
print ('各 feature 的重要性：%s' % rfc.feature_importances_)
importances = rfc.feature_importances_
std = np.std([tree.feature_importances_ for tree in rfc.estimators_], axis=0)
indices = np.argsort(importances)[::-1]# Print the feature ranking
print("Feature ranking:")
for f in range(min(20,xtrain.shape[1])):
print("%2d) %-*s %f" % (f + 1, 30, xtrain.columns[indices[f]], importances[indices[f]]))# Plot the feature importances of the forest
plt.figure()
plt.title("Feature importances")
plt.bar(range(xtrain.shape[1]), importances[indices], color="r", yerr=std[indices], align="center")
plt.xticks(range(xtrain.shape[1]), indices)
plt.xlim([-1, xtrain.shape[1]])
plt.show()
tuple(xtrain.columns[indices])
f, ax = plt.subplots(figsize=(7, 5))
ax.bar(range(len(rfc.feature_importances_)), rfc.feature_importances_)
ax.set_title("Feature Importances")
plt.show()
predictions_validation = rfc.predict_proba(xtest)[:,1]
fpr, tpr, _ = roc_curve(ytest, predictions_validation)
roc_auc = auc(fpr, tpr)
plt.title('ROC Validation')
plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % roc_auc)
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()