【OpenGL学习】transform

视图变换

进行视图变换的学习之前，首先需要明白为什么需要视图变换，一个模型在某种第三方软件（blender，maya，3Dmax…）被创建出的的时候，其顶点都是对应于自身所在的空间的，也就是模型空间（物体空间），但是最终显示在屏幕上对应的是屏幕空间，如果直接吧物体空间对应的坐标绘制到屏幕空间上，显然是不正确的，因此要通过变换将物体空间的坐标一步步变换到屏幕空间，才能得到正确的绘制结果。

一、坐标空间与空间转化

一个顶点从物体空间转化到屏幕空间，一般会经历下面几个空间坐标系：

• 模型（物体）空间(Object Space)

  局部空间是指物体所在的坐标空间，即对象最开始所在的地方。想象在一个建模软件（比如说Blender）中创建了一个立方体。创建的立方体的原点有可能位于(0, 0, 0)，即便它有可能最后在程序中处于完全不同的位置。甚至有可能创建的所有模型都以(0, 0, 0)为初始位置（译注：然而它们会最终出现在世界的不同位置）。所以，你的模型的所有顶点都是在局部空间中：它们相对于你的物体来说都是局部的。

• 世界空间(World Space)

  如果我们将我们所有的物体导入到程序当中，它们有可能会全挤在世界的原点(0, 0, 0)上，因为其顶点都是模型空间所对应的顶点。世界空间(world space)是一个宏观的特殊坐标系，其代表了我们关心的最大坐标系，每一个模型在世界空间中都对应着自己的位置，所以需要通过模型变换将模型的顶点转化到世界空间当中。一般包括：缩放，旋转，平移。

• 观察空间(View Space）

  观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。一般的操作是将摄像机移动到世界坐标的坐标原点，然后将摄像机的坐标和世界空间的坐标重合，注意要对所有的物体均做和相机相同的变化，这样才能保证物体和相机的相对位置不变。

• 裁剪空间(Clip Space)

  在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个特定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略，所以剩下的坐标就将变为屏幕上可见的片段。这也就是裁剪空间(Clip Space)名字的由来。通过投影变换，可以将观察空间对应的的坐标转化到裁剪空间当中，需要定义一个投影矩阵(Projection Matrix)，它指定了一个范围的坐标，比如在每个维度上的-1000到1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间，所以会被裁剪掉。

  一旦所有顶点被变换到裁剪空间，最终的操作——透视除法(Perspective Division)将会执行，在这个过程中我们将位置向量的x，y，z分量分别除以向量的齐次w分量；透视除法是将4D裁剪空间坐标变换为3D标准化设备坐标的过程。这一步会在每一个顶点着色器运行的最后被自动执行。

• 屏幕空间(Screen Space)

  屏幕空间（屏幕坐标Screnn Space）：就是屏幕的2d空间，大小就是屏幕的大小，以像素作为单位，可以设定屏幕大小，如常见的1024*768等等，0点在左上角，向右为x正向，向下为y正向

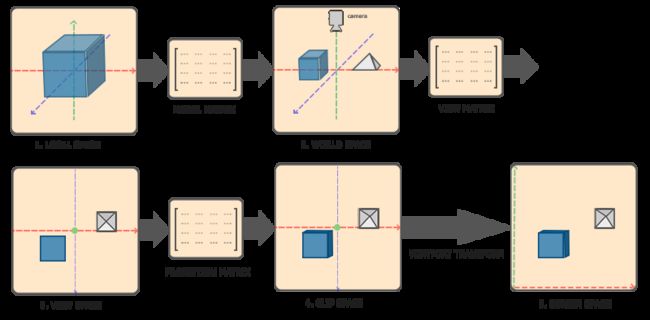
下面这幅图展示了顶点变化的整个过程：

其中从模型空间转化到世界空间对应的变换矩阵为 模型矩阵（Model Matrix） ，从世界空间转化到观察空间对应 视图矩阵（View Matrix） ，从观察空间转化到裁剪空间对应 投影矩阵（Projection Matrix），三个矩阵共同组成了我们熟悉的 MVP 矩阵。一个位于模型空间的顶点坐标，乘上这个矩阵之后，将会转化到裁剪空间。有关投影和变换，可以看这篇文章：图形学基础 - 变换 - 投影，大佬讲解的非常详细。

二、创建MVP矩阵

首先创建一个模型矩阵。这个模型矩阵包含了位移、缩放与旋转操作，它们会被应用到所有物体的顶点上，以变换它们到全局的世界空间。让我们变换一下我们的平面，将其绕着x轴旋转，使它看起来像放在地上一样。这个模型矩阵看起来是这样的：

//model
	glm::mat4 model = glm::mat4(1.0f);
	model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));

接着需要创建一个观察矩阵。我们想要在场景里面稍微往后移动，以使得物体变成可见的（当在世界空间时，我们位于原点(0,0,0)）。

我们自然不可能在场景中真的去移动摄像机，因为摄像机在场景中一般是没有实体的，但是将摄像机向后移动，和将整个场景向前移动是一样的，所以，观察矩阵所做的，以相反于摄像机移动的方向移动整个场景，因为最终的矩阵是作用在场景中的所有顶点上的。

OpenGL是一个右手坐标系(Right-handed System)，要沿着z轴的正方向移动是通过将场景沿着z轴负方向平移来实现。它会给我们一种我们在往后移动的感觉。

观察矩阵定义如下：

//view
	glm::mat4 view = glm::mat4(1.0f);
	view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));

然后定义一个透视投影矩阵：

//projection
	glm::mat4 projection = glm::mat4(1.0f);
	projection = glm::perspective(glm::radians(45.0f), (float)screen_width / (float)screen_height, 0.1f, 100.0f);

glm 中的 perspective 矩阵会帮我们创建并返回一个透视投影矩阵，该函数需要我们传入视场角FOV，屏幕的宽高比，以及近平面和远平面的距离。

然后计算得到我们的 MVP 矩阵，注意矩阵结合的顺序为从右到左：

glm::mat4 mvp = projection * view * model;

然后把该矩阵传入顶点着色器当中，在shader中添加 uniform 变量，并进行设置：

uniform mat4 u_mvp;
gl_Position = u_mvp * vec4(a_Position, 1.0);

triangle_shader.set_mat4("u_mvp", mvp);

这样传入片元着色器中的顶点就位于屏幕空间当中了。

运行一下看看结果：

看起来像一个斜躺着的木板，静止在一个虚构的地板上。

三、绘制3D图形

接下来绘制一个箱子来展示3D效果，首先准备好用于绘制箱子的顶点数组：

//Box vertices
	float box_vertices[] = {
	-0.5f, -0.5f, -0.5f,  0.0f, 0.0f,
	 0.5f, -0.5f, -0.5f,  1.0f, 0.0f,
	 0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
	 0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
	-0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
	-0.5f, -0.5f, -0.5f,  0.0f, 0.0f,

	-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
	 0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
	 0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
	 0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
	-0.5f,  0.5f,  0.5f,  0.0f, 1.0f,
	-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,

	-0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
	-0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
	-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
	-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
	-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
	-0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

	 0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
	 0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
	 0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
	 0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
	 0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
	 0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

	-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
	 0.5f, -0.5f, -0.5f,  1.0f, 1.0f,
	 0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
	 0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
	-0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
	-0.5f, -0.5f, -0.5f,  0.0f, 1.0f,

	-0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
	 0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
	 0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
	 0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
	-0.5f,  0.5f,  0.5f,  0.0f, 0.0f,
	-0.5f,  0.5f, -0.5f,  0.0f, 1.0f
	};

然后这次我们使用glDrawArrays来进行36个顶点的绘制（注意要重新指定顶点的布局，现在我们的顶点属性当中没有颜色了！）：

glDrawArrays(GL_TRIANGLES, 0, 36)

运行之后大概可以达到这样的效果：

为了更直观的观察绘制的效果，我们让这个箱子转起来，在Render Loop中加入：

		model = glm::rotate(model, glm::radians(0.5f), glm::vec3(0.5f, 1.0f, 0.0f));

在每一帧中都使这个箱子进行旋转，得到的结果如下：

很明显这个绘制结果是不正确的，这是因为绘制顺序不对的原因，正常情况应该先绘制后面的部分，再绘制前面的部分，要实现正常的效果，则需要打开深度测试，使用函数glEnable(GL_DEPTH_TEST); 开启深度测试，然后每次循环的时候将深度缓冲清空：

		glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

现在的结果就正确了：

现在可以在一个渲染循环中绘制多个箱子，首先先准备一个位置数组，为每个立方体定义一个位移向量来指定它在世界空间的位置。在一个glm::vec3数组中定义10个立方体位置：

//cube position
	glm::vec3 cube_position[] =
	{
		glm::vec3( 0.0f,  0.0f,  0.0f),
		glm::vec3( 2.0f,  5.0f, -15.0f),
		glm::vec3(-1.5f, -2.2f, -2.5f),
		glm::vec3(-3.8f, -2.0f, -12.3f),
		glm::vec3( 2.4f, -0.4f, -3.5f),
		glm::vec3(-1.7f,  3.0f, -7.5f),
		glm::vec3( 1.3f, -2.0f, -2.5f),
		glm::vec3( 1.5f,  2.0f, -2.5f),
		glm::vec3( 1.5f,  0.2f, -1.5f),
		glm::vec3(-1.3f,  1.0f, -1.5f)
	};

然后在 Render Loop 中，循环绘制10个立方体：

	rectangle_vertex_array->bind();
		for (unsigned int i = 0; i < 10; i++)
		{
			model = glm::mat4(1.0f); //必须每次还原model变量，不然最后的model还是根据原先的基础上变换的
			model = glm::translate(model, cube_position[i]);
			float angle = 20 * i;
			model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
			glm::mat4 mvp = projection * view * model;
			triangle_shader.set_mat4("u_mvp", mvp);
			glDrawArrays(GL_TRIANGLES, 0, 36);
		}
		

绘制结果如下：