全排列的非递归算法

利用堆栈消除递归练习二
从1~n这n个整数中取m个整数的全排列的递归算法很容易写出来，下面研究如何用堆栈消除递归。首先我们分析一下递归算法的思路：

//全排列递归算法
void perm(int flag[], int a[], int k, int n, int m)  /*递归算法*/ 
{ int i;
  if(k==m)
   { for(i=0;i<m;i++) printf("%d ", a[i]);
     printf("\n");
     return;
  }
  for(i=0;i<n;i++)
   if(flag[i]==0)
     { a[k]=i+1;
       flag[i]=1;
       perm(flag, a, k+1, n, m);
       flag[i]=0;
     }
}

从图中我们可以看出，解决全排列的问题关键就是将问题不断分解为小问题，当确定第一位时，只需要考虑后面n-1位的全排列，以此类推。

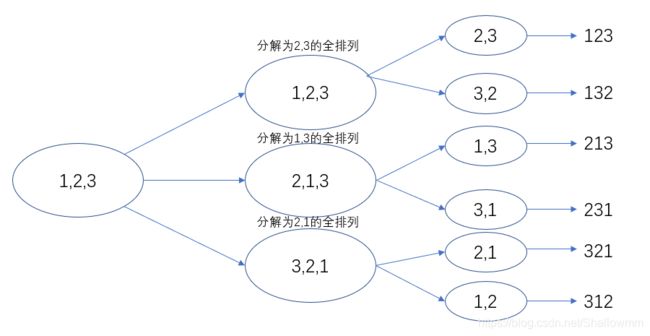
使用堆栈解决就没有这么简单了，但基本思路还是类似的，我们需要设置一个flag数组来存放每个元素是否可用的标志。当flag[i] = 1,代表可以使用，将其入栈。每次入栈需要将flag[i]设为0并将i置为-1，从头开始扫描是否有可用的元素。

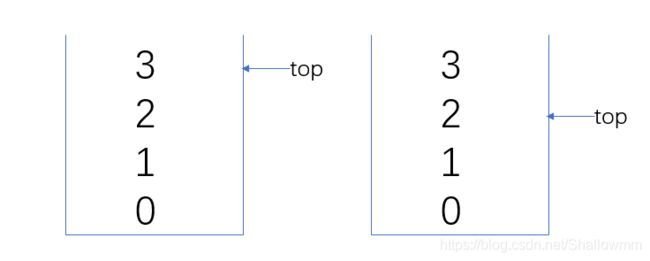
情况一：当top= m时，说明栈满。如图所示，此时将元素2弹出，变得重新可用，此时设i = 2，flag[i] = 1。

情况二：当i=n时，没有元素可以使用，此时需要进一步判断

1. top = 0, 此时栈是空的，则退出循环。
2. 由于没有元素可以使用了，所以这条路走到尽头了，我们需要再退一次栈，比方说123这个排列，之前由于栈满将3弹出，但是3后面已经没有元素可以使用，我们就要将2也弹出来，接下来要输出的就是132了。

情况三：i != n，flag[i] = 1，这种情况我们只需要将i元素入栈 ，然后flag置为0，i置为-1，从头扫描。

经过上面的分析，我们已经将非递归算法的思路解决了。

最后附上实现代码：

#include 
using namespace std;

void printStack(int stack[], int n){
  for (int i = 0; i < n; i++){
    cout << stack[i] + 1;  //因为i是从零开始的 所以每个都要加一
  }
  cout << endl;
}

void perm(int flag[], int n, int m){  //排列数的非递归算法
  int stack[20];  
  int top = 0;  //栈顶指针 指向栈顶下一个元素
  int i = -1;  

  while(1){
    ++i;
    if(i == n){  //当i=n时 没有元素可以再用 
      if(top == 0) break;  //栈为空时 退出循环
      else{
        top--;
        i = stack[top];
        flag[i] = 1;
      }
    }
    else if(flag[i] == 1){  //flag=1 则可用 入栈
      stack[top] = i;
      top++;
      flag[i] = 0; //元素已经不可用
      i = -1;
    }
    if(top == m){  //栈满 输出元素
      --top;  //退栈
      i = stack[top];  //将弹出的栈顶元素赋给i
      flag[i] = 1;  //元素被弹出 所以此时可用 flag置为1
      printStack(stack, m);  //输出一种排列
    }
  }
}

int main()
{
  int flag[20];
  for (int i = 0; i < 20; i++){
    flag[i] = 1;
  }
  perm(flag, 3, 3);
}