基于matlab数据线性拟合回归
1 选题背景及意义
在统计学中,线性回归是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。线性回归分析主要用来分析观测值x与y并拟合出一个合理的模型,当出现一个新的数值时,可以通过这个模型来预测出其对应数值。在高层次的运用时,线性回归分析可以用来量化y与大量x之间相关性的强度,推测与y不相关的x及部分冗余信息。
线性回归有很多实际用途。分为以下两大类:如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。另外,给定一个变量y和一些变量X1,.. . ,Xp,这些变量有可能与y相关,线性回归分析可以用来量化y与Xj之间相关性的强度,评估出与y不相关的Xj,并识别出哪些Xj的子集包含了关于y的冗余信息。线性回归模型经常用最小二乘法来拟合,但他们也可能用别的方法来拟合,比如用最小绝对误差回归,或者在桥回归中最小化最小二乘损失函数的惩罚
为此,具体问题中认识线性回归分析非常重要,注意比较与观测值之间的联系与区别,探索参数之间的联系,全面的辨证地分析问题,不为假想所迷惑,寻求问题的内在联系,从对实际问题的分析中学会利用图形分析、解决问题及用具体的数量来衡量两个变量之间的联系,线性回归模型能正确的用图形、数据和函数来描述变量的关系,在现实生活中的重要作用和实际价值。
2 总体设计思路
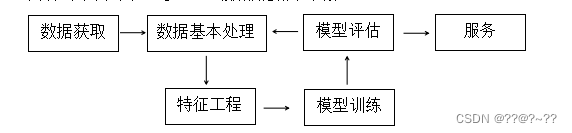
对于基本的模型的建立流程如下框图,首先就是进行数据获取,然后进入模型建立的第一步数据基本处理,第一步通常与第二步的特征工程相混淆,其实两步是不一样的,然后就是进行模型训练,最后进行模型评估,主要就是通过评估参数进行评价,如果评估合格后就可以进行工作了。否则就会重新进行数据处理再重新进行循环。拟合函数就是进行一个最基本的模型训练,然后为人所用。
在MATLAB中对于线性拟合的函数有很多种,其中regress最为常见而且函数的使用不仅方便还很准确。在b=regress(y,X)表达中;根据输入参数y与X,用最小二乘法求线性回归系数b,得到回归方程,值得说明的是X可以是一项和多项,一项的话得出的b就是两相,拟合方程就是一元线性方程,多项的话就会变成多元线性拟合方程。两者的不同对于regress函数都能精准求解。
文章通过两部分分别对regress函数的一元和多元进行拟合,并且对所采集的数据集进行模型评估。另外通过机器学习的方法进行拟合并且对数据集进行预测。机器学习的方法在matlab中有很好的应用,软件的模型库多种多样,我们把数据添加到软件的模块中,系统就能计算出最优的拟合模型,并且建立属于给定数据的模型,我们只需要把想要预测的数据添加到模型中就能进行预测十分方便。
3各模块设计方案与实验结果
一、一元拟合
一元线性拟合下b=regress(y,X)函数,X的变量只有一列,得出的b只有两个,b(1)为常数,b(2)为系数。表达式为Y=b(1)+b(2)X。另外regress函数还可以表达成下面的形式。[b,bint,r,rint,stats]=regress(y,X):意思是得到参数b的95%置信区间bint,残差r以及残差95%置信区间rint,stats有三个分量的向量,分别是决定系数R平方、F值以及回归的p值。
基于上面的理论基础进行代码编写,如下图所示,一组数据共有30个变量,需要对此数据做一元线性回归分析y=b1+b2*x,若只想得出线性回归模型,而不做其他分析只需调用b=regress(y,X);程序代码如下
图1 变量输入和数据处理
在对此部分进行运行后就可以在工作区找到b[],其中得出b=[27.2305 1.0220],但是我们并不能直观的看见拟合线和数据进行对比,所以根据b建立一元线性方程,在把数据的散点添加在图像中进行直观对比。代码如下
图2 输出图像
在下面的图像中可以直观的看见散点和曲线,显然散点都是均匀的分布在直线的周围,感觉拟合的准确率会很高,为了验证曲线的拟合优劣就可以用stats函数。stats中R平方来说明其拟合优劣,R平方越大拟合程度越高。
图3 散点图和回归曲线
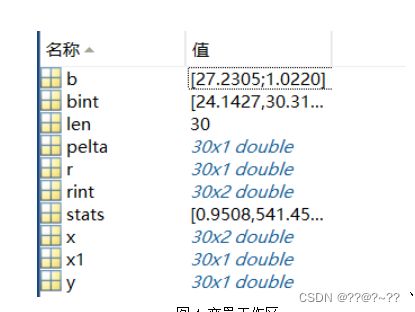
在regress函数中,按照需要调用[b,bint,r,rint,stats]=regress(y,X);返回更为复杂的数据,用来分析模型。因为在第一张代码图片中就已经调用了上面的写法,所以stats函数值在工作区中就已经能看见结果了,如图拟合优度为95%。很准确了。
图4 变量工作区
还有另一种方法,就是使用rcoplot(r,rint)函数做残差分析图,以及画出预测及回归线图,结果如图所示。从图中可以看出回归方程的拟合程度,还是非常好的。
图5 残差图
- 多元拟合
还是应用于regress函数,多元线性拟合下b=regress(y,X)函数,X的变量有多列,得出的b有多个,b(1)为常数,b(2)....为系数。表达式为Y=b(1)+b(2)X+...。在这里我们选取了三组单向打分成绩和综合打分成绩对应。对数据进行处理并且进行预测,代码如下图。
为了对拟合线和数据点进行直观的对比,我们也用代码对数据点和拟合线进行图像输出,代码如下,得到图像8。
图8 拟合曲线和数据变量图
同上在工作区中,其中stats中的第一个数是拟合优度,在这个模型中拟合优度为0.94903。拟合数据准确。
三、机器学习拟合
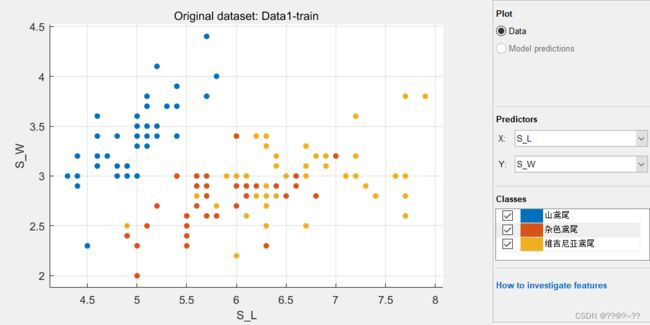
MATLAB中也有许多成型的模块可以进行数据拟合和预测,主要是通过机器学习的算法进行预测,经典的是对鸢尾进行预测,在这部分应用MATLAB APP中的Classification Learner进行训练拟合,首先将Data数据导入工作区,Data数据的输入可以是在工作区或者文件输入,注意的是五列数的表头应明确,作为学习值,第五列的数作为响应值,得出下面的数据图。
然后进行模型训练,为了对比所有的模型的结果,我选择的全部模型进行训练,如下图。
图10 选择所有模型训练
在训练完成后,各个模型的训练结果如下图,我只截取了一部分,在图中linear SVM的训练结果最高,准确率为97%,接下来选择这个模型进行数据分析。
图11 各个模型的准确率
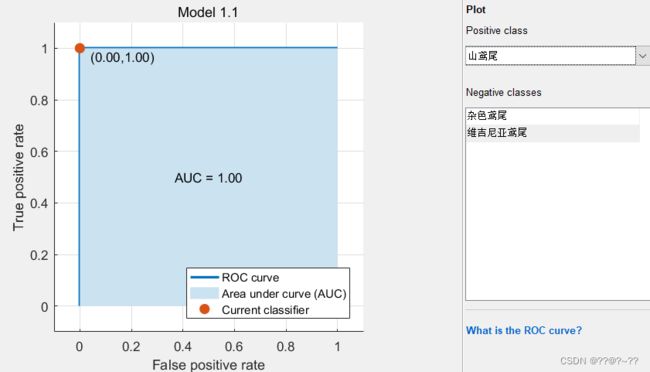
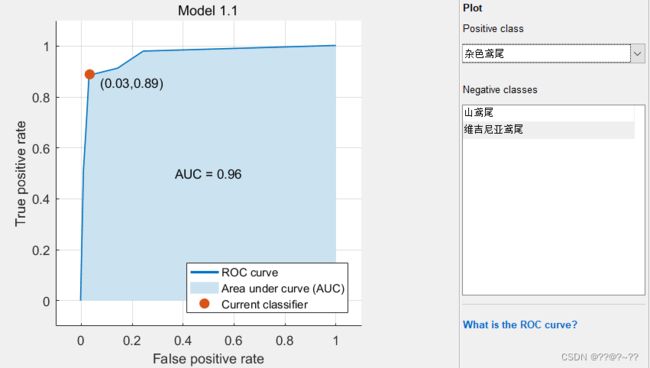
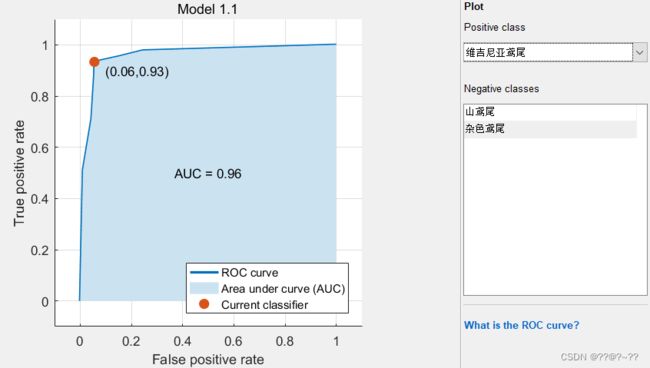
在linear SVM模型中,下三图中表示的是三个变量的ROC曲线图,表达的含义是对这个变量预测的准确率,图是山鸢尾的预测准确率, 图和图表示模型对他的预测准确率为100%,另外的两个杂色鸢尾和维吉尼亚鸢尾的准确率都为96%
图12 山鸢尾
此时MATLAB已经将训练的模型建立起来了,可以通过模型进行新数据的预测,选择最优的函数,把测试数据输入得出预测结果。
图15 命令行输入
将预测数据Data1输入进模型中按下回车后得到如下预测结果,值得说明的是Data1数据需要在工作区中为列表形式并且需要和Data的数据表的表头一致。
图16 结果输出
4总结
MATLAB具有强大的数据处理能力,在这三种方法对数据的拟合中都表现了良好的拟合优度,例如多元线性拟合和机器学习拟合的优度分别为95%和97%,已经十分准确了。证明两者的方法和模型建立的都是十分准确的,对数据处理有很大的帮助。但是在上述的模型中所选的数据很规整,而在实际的工程应用中数据不是这样的,所以如果想做好模型还需要在训练前做好数据处理和特征工程这两项工作。
5心得体会
在此次对MATLAB的学习中,感谢老师的耐心讲解。我了解matlab的强大,可以用于数据分析、无线通信、深度学习、图像处理等等的工程应用中,并且通过上面的三种数据拟合方法的操作,明白了一元线性拟合,多元线性拟合和机器学习拟合三种线性拟合的方式,对数据进行了拟合处理基本原理,了解了三种方法的准确率,方便性,主要是熟悉了MATLAB的工作流程和实际操作方法,能做到了为自己使用。学了本门课程之后对我的学习也有很大的帮助,不仅可以进行复杂的数学计算,还帮助我在阅读文献时遇到不懂得地方可以动手操作,加深理解。
clc;clear;close all;
x1=[17 16 21 20 25 25 26 27 29 28 29 30 31 32 34 35 35 36 37 38 38 39 39 40 42 41 41 46 48 51]';
y=[38.7 41.4 51.5 51.8 52.3 53.9 54.7 56.6 57.1 55.2 57.5 56.5 58.5 59.4 60.2 61.5 62.4 63.8 65.8 66.4 66.9 67.9 65.9 69.1 70.9 71.9 72.7 74.6 72.8 76.9]';
len = length(y);
pelta = ones(len,1);
x = [pelta, x1];
[b,bint,r,rint,stats]=regress(y,x); %调用回归函数求模型参数
plot(x1,y,'rp');%原始数据散点图
title('原始散点图');
rcoplot(r,rint);
title('残差图');
xlable('数据');
ylable('残差');
z=b(1)+b(2).*x1;%回归模型
figure;
plot(x1,y,'rp',x1,z,'b');%散点图和回归线
title('散点图和回归线');
%%
%多元回归分析
clc;clear;close all;
x1 = [180 201 205 208 213 217 218 222 226 230 233 238 240 242 253]'; % 跳高成绩
x2 = [280 240 226 224 220 217 225 221 211 213 199 198 195 186 183]'; % 1000m成绩
x3 = [153 170 162 160 162 165 170 168 169 179 172 172 175 181 176]'; % 跳绳个数
Y = [60 75 70 70 75 75 85 80 80 85 90 90 90 95 95]'; % 综合打分
% 因为用的3是维拟合,则 x 应该为 3*15 的矩阵,第一列为 1 ,第二列为 x1 ,第三列为 x2 , 第四列为 x3
% 15代表的是 样本个数
len = length(Y);
pelta = ones(len,1);
x = [pelta, x1, x2, x3];
[b,bint,r,rint,stats]=regress(Y,x); % 95%的置信区间
% b回归系数估计值 bint的置信区间 r 残差 rint的置信区间
%检验回归模型的统计量 拟合优度 R2,对方程整体显著性检验的F检验 p值 误差方差的估计值s^2
Y_NiHe = b(1)+b(2).*x1+b(3).*x2+b(4).*x3 ;%非线性
figure(1);
hold on;
plot(x1,'bo-');
plot(x2,'ro-');
plot(x3,'go-');
plot(Y,'mo-');
plot(Y_NiHe,'kx-','LineWidth',1);
legend('跳高成绩(cm)','1000m成绩(s)','跳绳个数','去年的综合分数(100分制)','多元线性回归拟合曲线')
str = num2str(stats(1,1));
disp(['拟合优度为:',str])