【深度学习常见问题——NMS】

用途

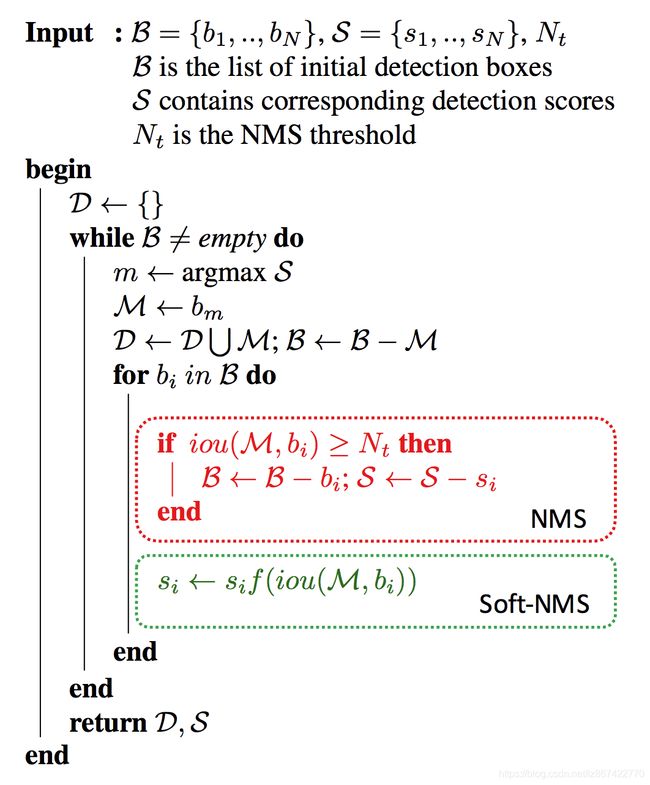
目标检测网络中，不论one-stage还是two-stage，都会产生超量的目标检测框，很多都指向了同一个目标，因此需要通过极大值抑制(Non Maximum Suppression)算法来筛选掉多余的检测框，找到每个目标最优的检测框

NMS

具体步骤

1. 设置一个IOU阈值，通常为0.5
2. 按照置信度将候选框进行降序排列
3. 将候选框中置信度最高的框A移除，并添加到输出结果列表中
4. 将候选框中与A的IOU超过阈值的框都删掉不考虑
5. 重复3，4两步，直到候选框列表为空

实现代码

def nms(bboxes, iou_thr):
    """
    Steps:
    1. 按照score排序bbox
    2. 选择最大score的bbox，放入predict_bboxes中
    3. 将bboxes中IOU>iou_thr的bbox删掉
    
    Args: 
    bboxes(list): (n, x1,y1,x2,y2,conf)-[n, left, top, right, bottom, score]
    iou_thr(int): step3中筛选IOU的标准
    
    Returns:
    predict_bboxes(list): (m, x1, y1, x2, y2, conf)筛选后的bbox
    """
    if len(bboxes) == 0:
        return []
    
    predict_bboxes = []
    bboxes = np.array(bboxes)
    
    # 计算bbox各自的面积
    x1 = bboxes[:, 0]
    y1 = bboxes[:, 1]
    x2 = bboxes[:, 2]
    y2 = bboxes[:, 3]
    scores = bboxes[:, 4]
    areas = (x2-x1+1) * (y2-y1+1)
    
    # Step1 按照score排序bbox
    order = np.argsort(scores) #np.argsort默认从小到大
    
    while order.size > 0:
        # Step2 选择当前置信度最高的bbox
        index = order[-1]
        predict_bboxes.append(bboxes[index])
        
        # Step3 计算选中的bbox与其他bbox的IOU，进行筛选
        # 计算IOU
        x11 = np.maximum(x1[index], x1[order[:-1]])
        y11 = np.maximum(y1[index], y1[order[:-1]])
        x22 = np.minimum(x2[index], x2[order[:-1]])
        y22 = np.minimum(y2[index], y2[order[:-1]])
        inter_w = np.maximum(0.0, x22-x11+1)
        inter_h = np.maximum(0.0, y22-y11+1)
        inters = inter_w * inter_h
        ious = inters / (areas[index] + areas[order[:-1]] - inters)
        
        # 筛选
        left = np.where(ious < iou_thr)
        order = order[left]
    return predict_bboxes

缺点

如果两个目标是交叠的，甚至是包含关系的，那NMS会把其中一个目标的bbox筛掉而导致漏检测。

Soft-NMS

针对于两目标交叠的情况做出了改进，在IOU大于阈值时不是直接将框删除，而是通过衰减其置信度的方式让其优先级靠后，但是保留了其被输出的可能性。

具体步骤

1. 设置一个IOU阈值，通常为0.5
2. 按照置信度将候选框进行降序排列
3. 将候选框中置信度最高的框A移除，并添加到输出结果列表中
4. 将候选框中与A的IOU超过阈值的框都删掉不考虑 进行置信度衰减，衰减方式为：
   $s_i=s_i(1-IOU(A,b_i)),iou(A,b_i)<threshold$
5. 重复3，4两步，直到候选框列表为空

于原版NMS方法的比对伪代码如下：

实现代码

def soft_nms(bboxes, Nt=0.3, sigma2=0.5, score_thresh=0.3, method=2):
    # 在 bboxes 之后添加对于的下标[0, 1, 2...], 最终 bboxes 的 shape 为 [n, 5], 前四个为坐标, 后一个为下标
    res_bboxes = deepcopy(bboxes)
    N = bboxes.shape[0]  # 总的 box 的数量
    indexes = np.array([np.arange(N)])  # 下标: 0, 1, 2, ..., n-1
    bboxes = np.concatenate((bboxes, indexes.T), axis=1)  # concatenate 之后, bboxes 的操作不会对外部变量产生影响
    # 计算每个 box 的面积
    x1 = bboxes[:, 0]
    y1 = bboxes[:, 1]
    x2 = bboxes[:, 2]
    y2 = bboxes[:, 3]
    scores = bboxes[:, 4]
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)

    for i in range(N):
        # 找出 i 后面的最大 score 及其下标
        pos = i + 1
        if i != N - 1:
            maxscore = np.max(scores[pos:], axis=0)
            maxpos = np.argmax(scores[pos:], axis=0)
        else:
            maxscore = scores[-1]
            maxpos = 0
        # 如果当前 i 的得分小于后面的最大 score, 则与之交换, 确保 i 上的 score 最大
        if scores[i] < maxscore:
            bboxes[[i, maxpos + i + 1]] = bboxes[[maxpos + i + 1, i]]
            scores[[i, maxpos + i + 1]] = scores[[maxpos + i + 1, i]]
            areas[[i, maxpos + i + 1]] = areas[[maxpos + i + 1, i]]
        # IoU calculate
        xx1 = np.maximum(bboxes[i, 0], bboxes[pos:, 0])
        yy1 = np.maximum(bboxes[i, 1], bboxes[pos:, 1])
        xx2 = np.minimum(bboxes[i, 2], bboxes[pos:, 2])
        yy2 = np.minimum(bboxes[i, 3], bboxes[pos:, 3])
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        intersection = w * h
        iou = intersection / (areas[i] + areas[pos:] - intersection)
        # Three methods: 1.linear 2.gaussian 3.original NMS
        if method == 1:  # linear
            weight = np.ones(iou.shape)
            weight[iou > Nt] = weight[iou > Nt] - iou[iou > Nt]
        elif method == 2:  # gaussian
            weight = np.exp(-(iou * iou) / sigma2)
        else:  # original NMS
            weight = np.ones(iou.shape)
            weight[iou > Nt] = 0
        scores[pos:] = weight * scores[pos:]
    # select the boxes and keep the corresponding indexes
    inds = bboxes[:, 5][scores > score_thresh]
    keep = inds.astype(int)
    return res_bboxes[keep]
    

Softer-NMS

大体思路

NMS和Soft-NMS的默认前提都是：置信度最高的bbox就是最精确的，但是实际上可能不成立。本文关注两个问题：

1. 所有bbox都足够精确，无法确定哪一个
2. 具有高置信度的bbox不够精确

参考资料

1.非极大值抑制(nms)算法详解[python_CSDN_智能血压计的博客]