【车间调度】 FJSP的析取图模型
本系列为自己学习调度相关知识的记录,如有误请指出,也欢迎调度方向的小伙伴加我好友共同交流。
在FJSP中,存在循环排列的特性,即同一个工件的多道工序可以在同一台机器上连续或间隔加工。当FJSP中每道工序确定了加工机器之后,即转变为一般的作业车间调度问题。而析取图(disjunctive graph)模型是描述车间调度问题的一种重要形式。
析取图模型定义
G=(N,A,E)
- N是所有工序组成的节点集,其中0和*表示两个虚设的起始工序和终止工序,每个节点的权值等于此节点工序在对应机器上的加工时间
- A是连接同一个工件的邻接工序间的有向弧集,表示工序之间的先后加工顺序约束
- E是连接在同一台机器上相邻加工工序间的析取弧集。
下图是三个工件、三台机器和九道工序。
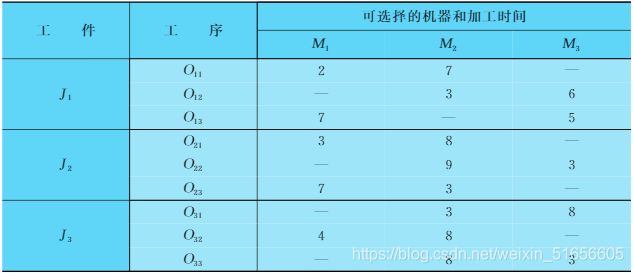
在此图中:节点集 N = { 0 , O 11 , O 12 , O 13 , O 21 , O 22 , O 23 , O 31 , O 32 , O 33 , ∗ } N=\{0,O_{11},O_{12},O_{13},O_{21},O_{22},O_{23},O_{31},O_{32},O_{33},*\} N={0,O11,O12,O13,O21,O22,O23,O31,O32,O33,∗}
有向弧集 A = { ( O 11 , O 12 ) , ( O 12 , O 13 ) , ( O 21 , O 22 ) , ( O 22 , O 23 ) , ( O 31 , O 32 ) , ( O 32 , O 33 ) } A=\{(O_{11},O_{12}),(O_{12},O_{13}),(O_{21},O_{22}),(O_{22},O_{23}),(O_{31},O_{32}),(O_{32},O_{33})\} A={(O11,O12),(O12,O13),(O21,O22),(O22,O23),(O31,O32),(O32,O33)}
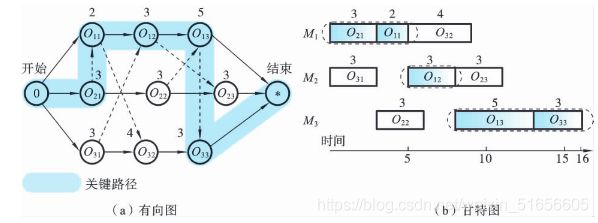
上图是一个可行调度方案,机器1上的选择 S 1 = { O 21 O 11 , O 32 S_1=\{O_{21}\,O_{11},O_{32} S1={O21O11,O32 机器2上的选择 S 2 = { O 31 , O 12 , O 23 } S_2=\{O_{31},O_{12},O_{23}\} S2={O31,O12,O23} 机器3上的选择 S 2 = { O 22 , O 13 , O 33 } S_2=\{O_{22},O_{13},O_{33}\} S2={O22,O13,O33}
在非循环有向图DS中,从起点0到终点*的最长路径称为关键路径(critical path),其长度等于该调度的最大完工时间。用析取图描述调度问题,就是为了找到此关键路径,并使之最小。属于关键路径上的每道工序称为关键工序。在同一台机器上紧邻的几个关键工序的组合称为关键块,同一个机器上可能有多个关键块,其中每个关键块的第一个工序为块首工序,每个关键块的最后工序称为块尾工序,其他称为内部工序.
O 21 , O 11 , O 12 , O 13 , O 33 O_{21},O_{11},O_{12},O_{13},O_{33} O21,O11,O12,O13,O33表示关键工序。
有两个关键块: { O 21 , O 11 } , { O 13 , O 33 } \{O_{21},O_{11}\},\{O_{13},O_{33}\} {O21,O11},{O13,O33}
关键路径的长度为16。
需要注意的是同一个调度方案可能存在多条关键路径。