I-BERT: Integer-only BERT Quantization(2021-1-5)
模型介绍
基于Transformer的模型,例如BERT、RoBERTa,在许多的自然语言处理任务中获得最优的结果。由于内存使用、推断延迟、能源损耗,以至于无法有效率的在边缘甚至数据中心进行推断。尽管量化是一个可行的解决方案,但是之前的一些基于Transformer的量化工作在推理阶段还是使用了浮点运算,不能有效地利用整数逻辑单元,比如最近的Turing Tensor Cores,或者传统的仅支持整型的ARM处理器。
I-BERT就是基于Transformer模型的新的量化方案,在整个推理期间都使用整数运算。 基于轻量整数近似方法来进行非线性操作,比如GELU,Softmax和LayerNormalization,I-BERT执行端到端仅整数的BERT推理,而无需进行任何浮点计算。
量化就是指参数或者激活函数用低精度位来表示。目前,所有基于Transformer模型的量化工作都使用的是模拟量化(simulated quantization),又叫做假量化(fake quantization)。这些工作中,部分或者全部的操作执行的还是浮点运算。这需要已经量化的参数或者激活函数通过浮点运算反量化到FP32类型。

如图所示,左边的图所有的操作都执行着浮点运算,参数已经被量化并保存为整型,但是在推理阶段需要反量化为浮点类型;中间的图只有一部分操作是整数运算,由于Softmax在这里执行的是浮点运算,故需要将输入的数据进行反量化且输出的数据需要量化为整型才能进行MatMul。右边就是I-BERT提出的只有整数的量化,可以看到,在整个推理期间既没有浮点运算也没有反量化。
模型改进
Basic Quantization Method
在均匀对称量化方案中,实数 x x x 被统一映射到一个整数 q ∈ [ − 2 b − 1 , 2 b − 1 − 1 ] q \in [-2^{b-1},2^{b-1}-1] q∈[−2b−1,2b−1−1],其中 b b b 指定了量化的位精度。用公式表示为:
q = Q ( x , b , S ) = I n t ( c l i p ( x , − α , α ) S ) q=Q(x,b,S)=Int (\displaystyle\frac {clip(x,-\alpha,\alpha)} S) q=Q(x,b,S)=Int(Sclip(x,−α,α))
其中, Q Q Q 表示量化操作, I n t Int Int 为整数映射(四舍五入到最接近的整数), c l i p clip clip 为截断函数, α \alpha α 为 c l i p clip clip 函数的参数用于控制离群值。 S S S 是一个比例因子,为 α / 2 b − 1 − 1 \alpha/2^{b-1}-1 α/2b−1−1。
相反的映射(又叫做反量化)是将一个量化后的值 q q q 变成实数,表示为:
x ~ = D Q ( q , S ) = S q ≈ x \tilde x=DQ(q,S)=Sq \approx x x~=DQ(q,S)=Sq≈x
其中, D Q DQ DQ 表示反量化操作。这种方法称为均匀对称量化,“均匀”是因为量化后的值和所映射的实数是一个常数。
Non-linear Functions with Integer-only Arithmetic
纯整数量化的关键是用整数算法执行所有运算,而不使用任何浮点计算。与线性操作(例如 MatMul)或分段线性操作(例如 ReLU)不同,这对于非线性操作(例如GELU、Softmax和LayerNorm)来说并不简单。这是因为之前的工作中的仅整数量化算法依赖于算子的线性性质。
例如,对于线性 MatMul 操作的 MatMul ( S q ) (Sq) (Sq) = S ⋅ S \cdot S⋅ MatMul ( q ) (q) (q)。这个性质允许我们将整数 MatMul 应用于量化的输入 q q q,然后将比例因子 S S S 相乘,得到与将浮点 MatMul 应用于去量化的输入 S q Sq Sq 相同的结果。但是,这个属性不适用于非线性操作,例如,GELU ( S q ) (Sq) (Sq) != S S S · GELU ( q ) (q) (q)。
一个简单的解决方案是计算这些操作的结果,并将它们存储在一个查找表中。然而,这种方法部署在芯片内存有限的芯片上可能会产生开销,并将产生与查找表执行速度成正比的瓶颈。另一种解决方案是将激活进行去量化,并将其转换为浮点运算,然后用单精度逻辑计算这些非线性操作。然而,这种方法并不只是集成的,也不能在不支持浮点运算的专门高效硬件上使用,例如,ARMCortex-M(ARM,2020)。
为了解决这一挑战,I-BERT 近似的非线性激活函数,GELU和Softmax,与多项式,可以用仅整数算术计算。计算多项式只包括加法和乘法,这可以用整数算法来完成。因此,如果能找到对这些操作的良好的多项式近似,那么就可以用仅使用整数的算术来执行整个推理。
例如,一个表示为 a ( x + b ) 2 + c a(x+b)^2+c a(x+b)2+c 的二阶多项式可以用仅整数算法有效地计算出来:
Polynomial Approximation of Non-linear Functions
关于用多项式近似一个函数有大量的工作。比如使用一类插值多项式,这里用一组函数值用于 n+1 个不同数据点 { ( x 1 , f 1 ) , . . . , ( x n , f n ) } \{(x_1,f_1),...,(x_n,f_n)\} {(x1,f1),...,(xn,fn)},然后试图找到一个最多 n 的多项式,在这些点上的函数值完全匹配。众所周知,存在一个唯一的多项式的次数最多为n,它通过所有的数据点。我们用 L 来表示这个多项式,定义为:
L ( x ) = ∑ i = 0 n f i l i ( x ) , l i ( x ) = ∏ 0 ≤ j ≤ n j ≠ i x − x j x i − x j \operatorname {L} (x)=\displaystyle \sum^n_{i=0}f_il_i(x) ,l_i(x)=\prod_{\substack {0 \le j \le n \\ j \ne i}} \frac {x-x_j} {x_i-x_j} L(x)=i=0∑nfili(x),li(x)=0≤j≤nj=i∏xi−xjx−xj
有趣的是,对于上面的问题,可以有两个旋钮来改变,以找到最好的多项式近似。由于知道实际的目标函数,并且可以查询任何输入的精确值,所以可以选择插值点 ( x i , f i ) (x_i,f_i) (xi,fi) 作为函数上的任何点。
第二个旋钮是选择多项式的次数。当选择一个高阶多项式会导致更小的误差时,在这方面有两个问题。
- 首先,高阶多项式具有更高的计算量和内存开销。
- 其次,用低精度的仅整数算法来计算它们是具有挑战性的,因为当将整数值相乘时可能会发生溢出。
对于每一个乘法,我们都需要使用双精度,以避免溢出。因此,挑战是找到一个好的低阶多项式,可以非常接近于在 Transformer 中使用的非线性函数。
Integer-only GELU
GELU是一个用于Transformer模型的非线性激活函数,用公式可以表示为:
GELU ( x ) : = x ⋅ 1 2 [ 1 + \operatorname {GELU} (x):=x \cdot \displaystyle\frac 1 2[1+ GELU(x):=x⋅21[1+erf ( x 2 ) ] , (\displaystyle\frac x {\sqrt 2})], (2x)], erf ( x ) : = 2 π ∫ 0 x exp ( − t 2 ) d t (x):=\displaystyle \frac 2 {\sqrt \pi} \int^x_0\exp(-t^2)dt (x):=π2∫0xexp(−t2)dt
这里 erf 是一个误差函数。

上图展示了GELU函数的表现,在很大的正负值的情况下,GELU和ReLU有相似的表现,但是在接近0时表现不一样。在 erf 函数中直接求积分项效率不高,因为这个原因,提出了一些近似函数来计算GELU。比如,有人用 sigmoid 函数来近似 GELU:
GELU ( x ) ≈ x σ ( 1.702 x ) \operatorname {GELU}(x) \approx x\sigma(1.702x) GELU(x)≈xσ(1.702x)
其中 σ \sigma σ 表示 sigmoid 函数,然而这个近似函数对于仅整数量化来说并不是一个可行的解决方案,因为 sigmoid 函数本身也是一个需要浮点运算的非线性函数。一种方式就是用所谓的 hard-sigmoid(h-sigmoid) 来近似 sigmoid,来获取对 GELU函数的仅整数近似:
h-GELU ( x ) : = x ReLU 6 ( 1.702 x + 3 ) 6 ≈ GELU ( x ) \operatorname {h-GELU}(x):=x \displaystyle \frac {\operatorname {ReLU}6(1.702x+3)} {6} \approx \operatorname {GELU}(x) h-GELU(x):=x6ReLU6(1.702x+3)≈GELU(x)
将这个近似函数称为 h-GELU 函数。尽管 h-GELU 可以用于整数计算,但是在 Transformer 中用 h-GELU 来替代 GELU 会导致结果有很大的精度丢失。这是因为 h-GELU 和 GELU 之间有很大的空隙,从上图(左)中也可以看出。
一种解决办法是使用多项式来近似 GELU 函数,通过解决下面的优化问题:
min a , b , c 1 2 ∥ GELU ( x ) − x 1 2 [ 1 + L ( x 2 ) ] ∥ 2 2 , s . t . L ( x ) = a ( x + b ) 2 + c \displaystyle \min_{a,b,c} \frac 1 2 \| \operatorname{GELU}(x)-x \frac 1 2[1+\operatorname{L}(\frac x {\sqrt 2})] \|^2_2, s.t. \operatorname {L}(x)=a(x+b)^2+c a,b,cmin21∥GELU(x)−x21[1+L(2x)]∥22,s.t.L(x)=a(x+b)2+c
这里,L(x) 是一个用于近似 erf 函数的二次多项式。直接优化上式会导致一个很差的近似,因为 erf 的定义域包含了所有的实数。为了解决这个问题,只优化 L(x) 使函数在一个限定的范围内,因为 erf 函数的 x 很大时,值接近1(-1)。利用 erf 是奇函数的性质(erf(-x) = -erf(x)),只考虑在正数域来近似它。当发现最佳的插值点 ( x i , f i ) (x_i,f_i) (xi,fi) 后,对多项式 L ( x ) (x) (x)进行一些调整,如下所示:
L ( x ) = sgn ( x ) [ a ( clip ( ∣ x ∣ , max = − b ) + b ) 2 + 1 ] \operatorname{L}(x)=\operatorname{sgn}(x)[a(\operatorname{clip}(|x|,\max=-b)+b)^2+1] L(x)=sgn(x)[a(clip(∣x∣,max=−b)+b)2+1]
这里 a = − 0.2888 , b = − 1.769 a = −0.2888,b = −1.769 a=−0.2888,b=−1.769,sgn 表示符号函数(sign)。i-GELU 是 GELU 的仅整数近似使用上述多项式,定义为:
i-GELU ( x ) : = x ⋅ 1 2 [ 1 + L ( x 2 ) ] \operatorname{i-GELU}(x):=x\cdot \displaystyle\frac 1 2 [1+\operatorname{L}(\frac x {\sqrt 2})] i-GELU(x):=x⋅21[1+L(2x)]
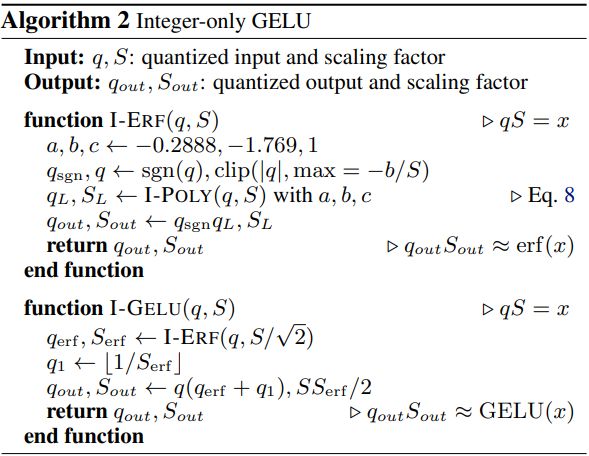
Algorithm 2 概括了使用 i-GELU 来近似计算 GELU 的过程,如下所示:
Integer-only Softmax
Softmax 函数规范化一个输入向量,然后转换成一个概率分布:
Softmax ( x ) i : = exp x i ∑ j = 1 k exp x j , x = [ x 1 , . . . , x k ] \operatorname{Softmax} (x)_i:=\displaystyle \frac {\exp x_i} {\sum^k_{j=1}\exp x_j}, x=[x_1,...,x_k] Softmax(x)i:=∑j=1kexpxjexpxi,x=[x1,...,xk]
用整数运算来近似 softmax 层是一个非常大的挑战,因为用在 softmax 上的指数函数是没有边界的并且改变的非常快。正因为如此,很多的 Transformer 量化技术在这一层还是使用浮点运算。之前的一些工作提出了用插值法查表,但是像之前一样还是要避免查表而应尽可能找一种纯粹的算数运算来近似。尽管有人提出用多项式来近似指数函数,但是这个多项式的次数很高,而且只适用于受限的定义域。
和 GELU 一样,不能使用高次多项式,甚至使用高次多项式来近似softmax函数是无效的。然而,通过限制 softmax 近似的范围可能解决这个问题。首先,从指数中减去输入数据的最大值使数值达到稳定。
Softmax ( x ) i = exp ( x i − x m a x ) ∑ j = 1 k e x p ( x j − x m a x ) \operatorname{Softmax}(x)_i=\displaystyle \frac {\exp(x_i-x_{max})} {\sum^k_{j=1}exp(x_j-x_{max})} Softmax(x)i=∑j=1kexp(xj−xmax)exp(xi−xmax)
这里 x max = max i ( x i ) x_{\max}=\max_i(x_i) xmax=maxi(xi)。注意这里所有的输出到指数函数( x ~ = x j − x m a x \tilde x=x_j-x_{max} x~=xj−xmax)的数都变成了负数。可以分解一些负实数 x ~ \tilde x x~ 为 x ~ = ( − ln 2 ) z + p \tilde x=(-\ln2)z+p x~=(−ln2)z+p,其中除数 z 是一个非负整数,p 是一个在 ( ln 2 , 0 ] (\ln2,0] (ln2,0] 的实数。指数函数 x ~ \tilde x x~ 可以写成如下形式:
e x p ( x ~ ) = 2 − z exp ( p ) = e x p ( p ) > > z exp(\tilde x)=2^{-z}\exp(p)=exp(p)>>z exp(x~)=2−zexp(p)=exp(p)>>z
其中>>是移位操作。因此,我们只需要在 p ∈ ( − l n 2 , 0 ] p∈(−ln2,0] p∈(−ln2,0] 的紧致区间中近似出指数函数。与所有实数的域相比,这是一个要小得多的范围。使用一个二阶多项式来近似在这个范围内的指数函数。为了找到多项式的系数,我们在 ( − l n 2 , 0 ] (−ln2,0] (−ln2,0] 的区间内最小化到指数函数的 L 2 L^2 L2 距离。这就导致了以下近似值:
L ( p ) = 0.3585 ( p + 1.353 ) 2 + 0.344 ≈ exp ( p ) \operatorname{L}(p)=0.3585(p+1.353)^2+0.344\approx\exp(p) L(p)=0.3585(p+1.353)2+0.344≈exp(p)
用这个多项式来替换上式的指数项就得到了 i-exp:
i-exp ( x ~ ) : = L ( p ) > > z \operatorname{i-exp}(\tilde x):=\operatorname{L}(p)>>z i-exp(x~):=L(p)>>z
其中, z = [ − x ~ / ln 2 ] , p = x ~ + z ln 2 z=[−\tilde x/\ln2],p=\tilde x+z\ln2 z=[−x~/ln2],p=x~+zln2。这可以用整数算法来计算。Algorithm 3 描述了使用 i-exp 的仅整数计算的softmax函数。从上面的图中也可以看出, i-exp 函数与指数函数几乎相同。这两个函数之间的最大差距只有1.9×10−3。考虑到单位区间的8位量化引入了1/256=3.9×10−3的量化误差,相对近似误差可以忽略不计,可以纳入量化误差中。
Integer-only LayerNorm
LayerNorm通常用于Transformers中,涉及一些非线性操作,如除法、平方和平方根。此操作用于通过channel维度来规范化输入的激活函数。标准化过程描述如下:
x ~ = x − μ σ , μ = 1 C ∑ i = 1 C x i , σ = 1 C ∑ i = 1 C ( x i − μ ) 2 \tilde x=\displaystyle \frac {x-\mu} {\sigma},\mu=\frac 1 C \sum^C_{i=1}x_i,\sigma=\sqrt {\frac 1 C\sum^C_{i=1}(x_i-\mu)^2} x~=σx−μ,μ=C1i=1∑Cxi,σ=C1i=1∑C(xi−μ)2
这里, µ µ µ 和 σ σ σ 是输入跨通道维度的平均值和标准差。这里的一个微妙挑战是,NLP任务的输入统计信息(即 µ µ µ 和 σ σ σ)变化迅速,这些值需要在运行期间动态计算。虽然计算 µ µ µ 很简单,但计算 σ σ σ 需要平方根函数。通过Algorithm 4中提出的迭代算法,可以用仅整数算法有效地计算平方根函数。该算法基于牛顿法迭代搜索 ⌊ n ⌋ \lfloor \sqrt n\rfloor ⌊n⌋ 的精确值,只需要整数运算。该算法在计算上是轻量级的,因为对于任何INT32输入,它最多可以在4次迭代中收敛,并且每次迭代只包含一个整数除法、一个整数加法和一个位移操作。而 LayerNorm 中的其他非线性运算,如除法和平方运算,则直接用整数算法计算。
模型参考
论文地址:https://arxiv.org/abs/2101.01321
代码地址1:https://github.com/huggingface/transformers/tree/master/src/transformers/models/ibert
代码地址2:https://github.com/kssteven418/I-BERT