stack、queue、priority_queue

容器适配器

适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结)，该种模式是将一个类的接口转换成客户希望的另外一个接口。

其中stack和queue都是容器适配器，其中stack可以封装vector、list以及我们后面要提到的deque，而由于queue是先进先出，所以实现的头删，因此封装的只有list和deque。

具体是怎么实现的我们在模拟实现的时候提一下

---

stack

template
class stack
{
public:
private:
	vector st;
};

想要实现封装，我们可以采用上面的方式，但我们在上面也提到了，stack可以封装的容器不止一种，因此，我们就可以把容器也作为一个模板参数

template
class stack
{
public:
private:
	Container _con;
};

而在源码中，为模板参数Container提供了一个缺省值为deque

template>
class stack
{
public:
private:
	Container _con;
};

 之后就只剩下类成员函数的实现了，stack常用的就那么几个empty、size、top、pop、push，前两个都是容器中现有的函数，而top、pop、push分别对应着back、pop_back以及push_back，而所封装的容器必须要有上面这些函数，这也就是为什么会选择vector、list和后面的deque

template>
	class stack
	{
	public:
		bool empty()
		{
			return _con.empty();
		}
		int size()
		{
			return _con.size();
		}
		const T& top() const
		{
			return _con.back();
		}

		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_back();
		}
	private:
		Container _con;
	};

---

queue

与stack类似，只是top变为了front和back，而push、pop对应push_back、pop_front

template>
class queue
{
public:
	bool empty() const
	{
		return _con.empty();
	}

	size_t size() const
	{
		return _con.size();
	}

	const T& front() const
	{
		return _con.front();
	}

	const T& back() const
	{
		return _con.back();
	}

	void push(const T& x)
	{
		_con.push_back(x);
	}

	void pop()
	{
		_con.pop_front();
	}
private:
	Container _con;

---

deque

deque，其实就是一个vector与list的结合，可以实现头删、头插、尾删、尾插。但说是结合，其实使用场景非常有限，所以我们就简单讲讲原理是什么样的

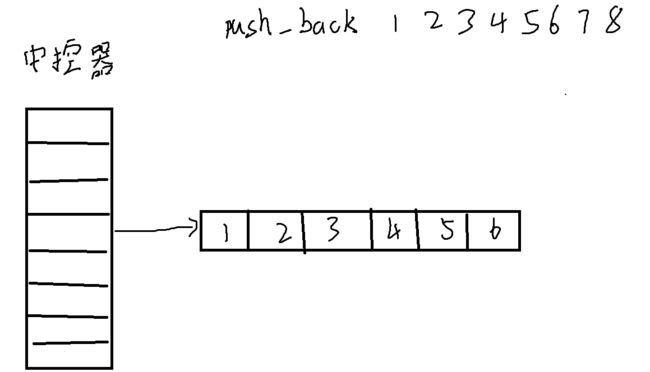
首先呢，deque内部有一个中控器，存放的是众多数组的首元素地址

而这些数组就是用来存放数据的，形式上有点类似于我们动态模拟的二维数组

这些数组的容量大小都是固定的，在一个数组没存满之前尾插依次在后面存放

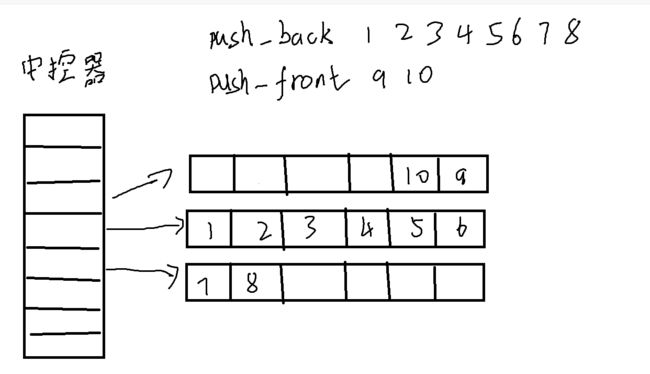
而在存满后，再进行尾插会开辟一个新的数组，地址存放在中控器的尾端的下面

 而若是进行头插，若是头部的数组满了，则开辟一个新的数组，地址存放在头部的上面

而无论满还是没满，都需要从后向前存放

这样，便可以实现头插、头删、尾插、尾删

与vector比较，deque的优势是：头部插入和删除时，不需要搬移元素，效率特别高，而且在扩容时，也不需要搬移大量的元素，因此其效率是必vector高的。

与list比较，其底层是连续空间，空间利用率比较高，不需要存储额外字段。

因此，deque才作为默认类去进行stack和queue的封装

同样，我们上面说了，deque具有很大的局限性：不适合遍历，因为在遍历时，deque的迭代器要频繁的去检测其是否移动到某段小空间的边界，导致效率低下，因此，deque才只适合类似于stack和queue这样的适配器。

---

priority_queue

它也是一种容器适配器，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。说人话就是一个大堆，而其实，它本质是一个堆，只是在模板参数中有一个决定大小比较的仿函数，而它的缺省值（less）决定了它是一个大堆，当然我们也以传入库中的另一个（greater）来使他称为小堆。

首先我们先来简单的使用一下

void test1()
{
	priority_queue heap1;
	heap1.push(1);
	heap1.push(3);
	heap1.push(4);
	heap1.push(2);
	while (heap1.size())
	{
		cout << heap1.top() << ' ';
		heap1.pop();
	}
	cout << endl;
	priority_queue,greater> heap2;
	heap2.push(1);
	heap2.push(3);
	heap2.push(4);
	heap2.push(2);
	while (heap2.size())
	{
		cout << heap2.top() << ' ';
		heap2.pop();
	}
}

其实，接口还是那么几个，size、empty、top、push、pop

而有一点需要注意，当存放自定义类型的数据的时候，由于greater、less内部需要进行大小比较，因此我们需要自己写一个less仿函数来传入特定的自定义类型的数据作比较

模拟实现

在二叉树中，我们已经对堆进行了讲解，所以关于内部接口的实现就稍微一提，我们需要注意的就是仿函数这一概念

堆

而仿函数本质上是一个类，拿less来说，在这个类中进行()的运算符重载（使其在形式上类似于函数），在重载中返回传入的两个数据所比较的结果

template
struct less
{
	bool operator()(const T& left, const T& right)
	{
		return left < right;
	}
};
template
struct greater
{
	bool operator()(const T& left, const T& right)
	{
		return left > right;
	}
};

由于这个类只需要在比较的这一行代码中起作用，因此我们在实例化时可以使用匿名对象

例如在比较父节点和子节点时

Compare()(c[parent], c[child])

之后，我们便只需要将之前堆学过的那些东西封装成接口，并将比较改用仿函数就可以了

namespace szt
{
	template
	struct less
	{
		bool operator()(const T& left, const T& right)
		{
			return left < right;
		}
	};

	template
	struct greater
	{
		bool operator()(const T& left, const T& right)
		{
			return left > right;
		}
	};

	template, class Compare = less>
	class priority_queue
	{
	public:
		priority_queue() : c() {}

		template
		priority_queue(Iterator first, Iterator last)
			: c(first, last)
		{
			int count = c.size();
			int root = ((count - 2) >> 1);
			for (; root >= 0; root--)
				AdjustDown(root);
		}

		void push(const T& data)
		{
			c.push_back(data);
			AdjustUP(c.size() - 1);
		}

		void pop()
		{
			if (empty())
				return;

			swap(c.front(), c.back());
			c.pop_back();
			AdjustDown(0);
		}

		size_t size()const
		{
			return c.size();
		}

		bool empty()const
		{
			return c.empty();
		}

		const T& top()const
		{
			return c.front();
		}
	private:
		void AdjustUP(int child)
		{
			int parent = ((child - 1) >> 1);
			while (child)
			{
				if (Compare()(c[parent], c[child]))
				{
					swap(c[child], c[parent]);
					child = parent;
					parent = ((child - 1) >> 1);
				}
				else
				{
					return;
				}
			}
		}

		void AdjustDown(int parent)
		{
			size_t child = parent * 2 + 1;
			while (child < c.size())
			{
				if (child + 1 < c.size() && Compare()(c[child], c[child + 1]))
					child += 1;

				if (Compare()(c[parent], c[child]))
				{
					swap(c[child], c[parent]);
					parent = child;
					child = parent * 2 + 1;
				}
				else
					return;
			}
		}
	private:
		Container c;
	};
}