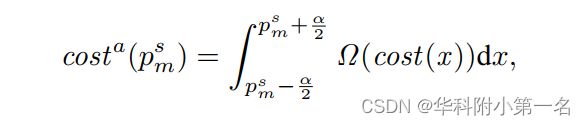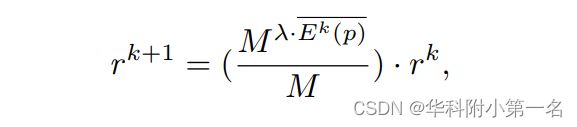【论文简述】EPP-MVSNet: Epipolar-assembling based Depth Prediction for Multi-view Stereo（ICCV 2021）

一、论文简述

1. 第一作者：Xinjun Ma、Yue Gong

2. 发表年份：2021

3. 发表期刊：ICCV

4. 关键词：MVS、极线、级联、可见性图、伪3D卷积

5. 探索动机：自MVSNet提出以来，基于正平扫(front-to-parallel)+可微单应性形变(differentiable homography)构建多视图对cost volume的learning-based方法在越来越多的公开数据集上证明了其优势。但是这类方法的预测精度和效率会极大地受到深度假设的影响，在深度范围较大的场景下难以达到计算量和精度之间的良好平衡。后续的CasMVSNet提出coarse-to-fine的结构范式，在小尺度特征上进行粗粒度全局深度范围下的预测，将refine的任务交给大尺度特征。coarse-to-fine的范式在一定程度上控制了整体的深度假设数量，因此能够在不过多增长计算量的情况下提升深度预测精度，但是依旧没有对深度假设的设置问题进行过多探讨。

• They still suffer from high memory and computation requirement for constructing and regularizing cost volumes, which make them unable to make fully usage of high resolution images.
• The memory and computation requirement of MVSNet is determined by the spatial resolution of the image and the depth resolution of the scene and the regularization network of multiple 3D convolution layers.

6. 工作目标：针对上述问题，华为MindSpore团队提出了一种针对深度假设进行合理设置的高精高效稠密重建算法EPP-MVSNet。

7. 核心思想：EPP-MVSNet继承了coarse-to-fine思想，在此基础上分别对于coarse阶段和fine阶段的深度假设分别提出了对应的EAM(epipolar assembling module)和ER(entropy refining strategy)模块进行优化。同时，通过对3D正则网络进行精简，进一步提升了整个模型的计算效率。

• We introduce an epipolar-assembling module for assembling high-resolution information into cost volumes with limited size.
• We propose an entropy-based process that adjusts depth range for reducing redundancy and information loss.
• We apply a light-weighted 3D regularization network which dramatically increases learning and inference efficiency.

8. 实验结果：SOTA

We have conducted extensive experiments on challenging datasets Tanks & Temples(TNT), ETH3D and DTU. As a result, we achieve promising results on all datasets and the highest F-Score on the online TNT intermediate benchmark.

9.论文&代码下载：

https://openaccess.thecvf.com/content/ICCV2021/papers/Ma_EPP-MVSNet_Epipolar-Assembling_Based_Depth_Prediction_for_Multi-View_Stereo_ICCV_2021_paper.pdf

http://https: //gitee.com/mindspore/mindspore/tree/m aster/model_zoo/research/cv/eppmvsnet

二、实现方法

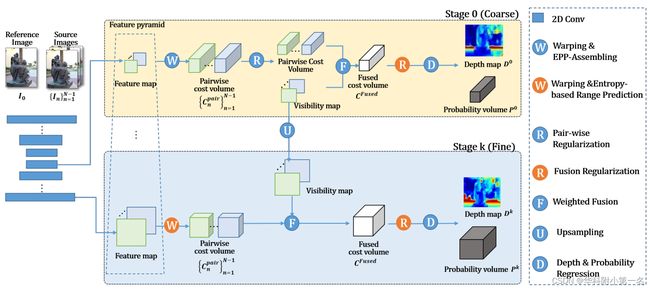
1. EPP-MVSNet概述

网络采用多阶段结构，从粗到细进行深度预测。在每个阶段k，通过特征提取、代价体构造、正则化和回归四个关键步骤推断深度图Dk和相应的概率体Pk。

1. 给定参考图像I0和源图像Ii，应用金字塔特征提取生成粗或细空间分辨率的特征图；
2. 特征图进行单应性变化，构建特征体；
3. 利用极线聚合模块和基于熵的改进策略进行粗阶段和细阶段的相关代价体构建；
4. 使用与伪3D CNN构成的轻量级网络对代价体进行正则化；
5. 对正则化的代价体进行回归，生成深度图和相应的概率图。

​2. 代价体构建

代价体是通过计算参考和源特征之间的相关来构建的。首先利用可微单应性变化构建特征体。然后，利用极线聚合模块（epepola-rassemble）计算参考特征与源特征体之间的匹配代价，并相应地在粗阶段和细阶段进行基于熵的改进，从而构建代价体。

3. 极线聚合模块

深度假设的设置作为大部分coarse-to-fine稠密重建方法的关键步骤，在不同的阶段的设置有着较大差别。其中，coarse阶段需要设置全局深度范围下的若干深度假设，同时为了控制cost volume的大小，该阶段往往只能设置一个相对较小的深度假设数量。这就导致了coarse阶段的深度假设间隔相对较大，具体反映到源视图上，呈现出对极线采样点分布相对稀疏的情况，容易遗漏关键特征点。

针对此问题，EPP-MVSNet提出了EAM(epipolar assembling module)模块，通过提前计算默认深度假设范围情况下辅助视图上原始采样点的分布情况，根据其分布间隔适应性地插入新的采样点。通过这个策略，EPP-MVSNet能够根据主视图和不同辅助视图之间由于空间几何关系不同产生的不同采样点分布情况，自适应地维持采样点的密集程度，减少遗漏关键特征点的可能。

如图3(a)所示，对于每个参考点pr，对应源点ps在不同深度假设dm沿极线离散采样。在粗阶段固定假设范围，可以通过增加假设数m来缩小采样源点之间的间隔，但这不可避免地会导致体的增长和较高的内存和计算成本。为此，通过将自适应区间的特征聚合到沿极极线分布的采样点上，打破利用高分辨率代价体的网络效率约束:

其中α表示采样点psm之间的间隔，Ω(·)表示极线聚合。对方程进行离散化，实现极线聚合模块。

自适应插值虽然增加了采样密度，但是不可避免地导致了cost volume的线性增长，同时也可能出现主视图和不同辅助视图生成的cost volume的形状不一的情况。为了控制cost volume的大小，EAM采用了“深度卷积“对插值后的cost volume进行简单的信息提取，之后根据插值情况选择不同窗口大小和步长设置的max pooling对cost volume进行降采样，使其变回插值之前的形状。同时，EAM的动态pooling还会将cost volume深度维度上插值点的cost信息汇聚到原始点上。

首先，利用深度假设dm的采样源点的位置，然后以半像素的最大间隔作为最优区间，沿极线插值偶数个点，通过测量参考点与密集插值点之间的群相关，构建高分辨率代价体。假设深度是使用逆深度设置生成的，因此采样点之间的间隔相对均匀。然后，通过图3(b)所示的网络聚合由内插点构成的代价体，来缩小代价体。该聚合网络由聚合和池化组成。考虑到高分辨率的代价体，每个体使用3×1×1核的卷积层来聚合邻近的特征，以获得适当的感受野。此外，通过沿深度方向的最大池化操作减小代价体，池化窗口大小自适应插值速率。

经过EAM模块处理后的代价体，依旧维持了原始形状，但是每个cost voxel都汇聚了邻近插值采样点的信息，其感受野要远优于处理之前，从而能够做出更为精准的深度预测。而且不仅充分利用了图像信息，而且不受相机位置多样性引起的深度间隔变化的影响，能自适应地以最优分辨率聚合特征。

4. 基于熵的改进策略

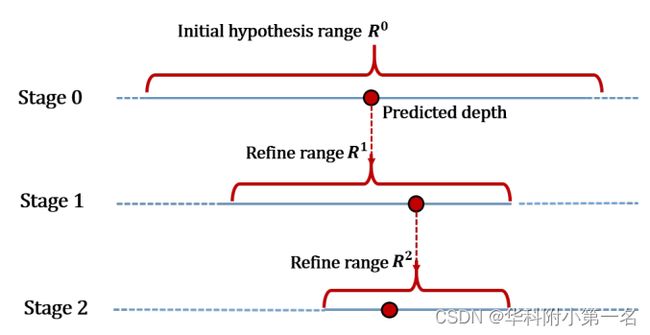
在refine阶段的深度假设一般以上个阶段的深度预测结果为中心，向两边各扩展一定区间作为深度假设范围，假设范围通常由实验确定的固定因素。由于refine阶段的深度预测基于高分辨率的特征，考虑到计算效率无法采用过多的深度假设。如果为了预测精度用一个固定的因子缩小统一缩小深度假设范围，可能导致前置阶段深度预测不准确而将真值排除在外；如果相对保守地放宽深度假设范围，又会引起深度间隔增大，从而导致预测精度下降。从粗至细的假设深度的变化如下：

针对上述问题，EPP-MVSNet提出了ER(entropy refining strategy)模块，可以根据当前阶段的深度预测情况自适应调整下个阶段的深度假设范围。ER模块利用了“熵”的性质，其表达了模型对于预测结果的置信度：熵越大，代表模型对于预测结果越不置信。

给定概率体Pk, k阶段深度预测的置信度由每个假设深度的预测概率熵估计：

如上述所示，E代表熵，k代表当前处于的阶段，M代表当前阶段的深度假设数量，P代表深度预测概率，p代表像素位置，d代表相应的深度假设。熵越大表示Dk的置信度越低，自然需要的假设深度范围越大。k+1阶段的假设深度范围由以下决定：

其中，r代表深度范围。计算得到当前阶段深度图上每个点对应的熵之后，根据上述公式获取下一个阶段的深度假设范围。由于深度图的置信度是通过简单地平均像素的熵来近似的， 因此引入了一个超参数λ来调整假设深度范围的缩小因子。ER模块可以根据每个阶段的深度预测情况自适应地确定下个阶段适宜的深度假设范围，从而进一步改进深度预测精度的同时，减少错误地将真值排除在深度假设范围之外的情况。

5. 轻量级正规化

EPP-MVSNet在代价体聚合上参考Vis-Mvsnet采用了加权聚合的方式，并利用soft argmin从代价体回归得到粗深度。同时为了节省计算量，只在coarse阶段生成作为权重的可见性图，后续阶段通过上采样的方式复用权重。

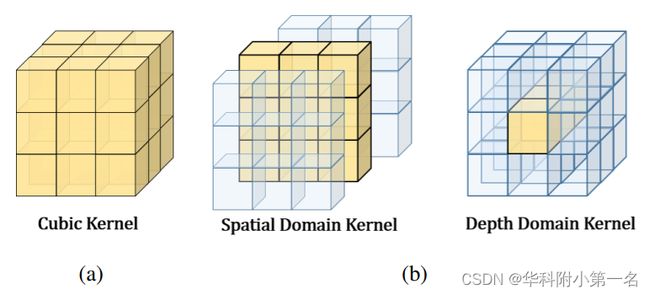
作者认为由正常立方卷积CNN得到的不同深度的相邻像素的代价体相干性差，计算冗余，成本高。因此，采用pseudo-3D卷积代替传统3D卷积。如下图所示，pseudo-3D分别在空间维度和深度维度上用CNN。对于核大小为1×3×3的空间卷积，对相邻像素的代价体进行卷积，在深度域上对不同深度假设下像素的代价体进行3×1×1的卷积。明显地降低了计算量，提高了重建质量。

6. 实验

6.1. 实现

通过PyTorch实现，使用DTU数据集训练，在DTU上测试。在blenddmvs数据集上训练，在Tanks-and-Temples和ETH3D上测试。在训练过程中，设置图像分辨率为512 × 640，源图像数量N = 3，输出深度图大小为256 × 320。采用三阶段结构，用各阶段深度图预测损失L1和粗阶段概率体不确定性损失[27]的总和进行训练。对于每个阶段，假设深度的数量为M1 = 32, M2 = 16, M3 = 8。使用Adam作为优化器，训练网络10个epoch，批处理大小为4。

6.2. 基准结果

为了进行评估，设置粗像素插值的间隔阈值为0.5，采用动态一致性检查方法从深度图生成点云。

DTU数据集基准、Tanks & Temples：SOTA

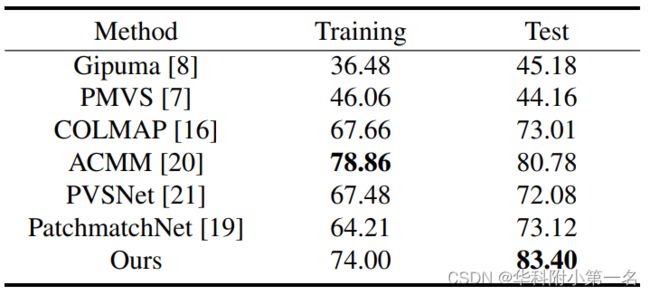
ETH3D：

6.3. 内存和运行时长比较

使用1920 × 1056的固定输入大小和相同的源图像数4