python 多元线性回归_多元统计分析之多元线性回归的R语言实现

多元统计分析之多元线性回归的R语言实现

多元统计分析--multivariate statistical analysis

研究客观事物中多个变量之间相互依赖的统计规律性。或从数学上说， 如果个体的观测数据能表为 P维欧几里得空间的点，那么这样的数据叫做多元数据，而分析多元数据的统计方法就叫做多元统计分析 。

重要的多元统计分析方法有:多重回归分析、判别分析、聚类分析、主成分分析、对应分析、因子分析、典型相关分析、多元方差分析等。

多元线性回归(普通最小二乘法)

用来确定2个或2个以上变量间关系的统计分析方法。多元线性回归的基本的分析方法与一元线性回归方法是类似的，我们首先需要对选取多元数据集并定义数学模型，然后进行参数估计，对估计出来的参数进行显著性检验，残差分析，异常点检测，最后确定回归方程进行模型预测。(1)做个简单线性回归热热身

women#使用自带的woman数据集

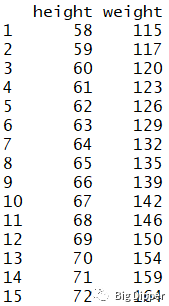
fit

summary(fit)#展示拟合模型的详细信息

women$weight#列出真值

fitted(fit)#列出拟合模型的预测值

residuals(fit)#列出拟合模型的残差值

coefficients(fit)#列出拟合模型的模型参数

confint(fit)#列出拟合模型参数的置信区间

anova(fit)#生成一个拟合模型的方差分析表，或者比较两个或更多拟合模型的方差分析表

vcov(fit)#列出拟合模型的协方差矩阵

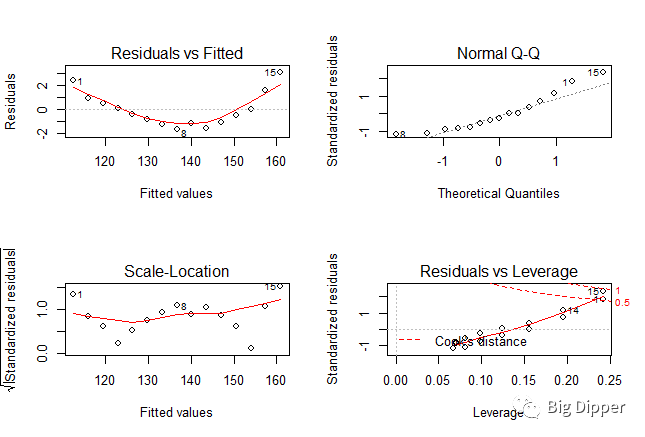
par(mfrow=c(2,2))

plot(fit)

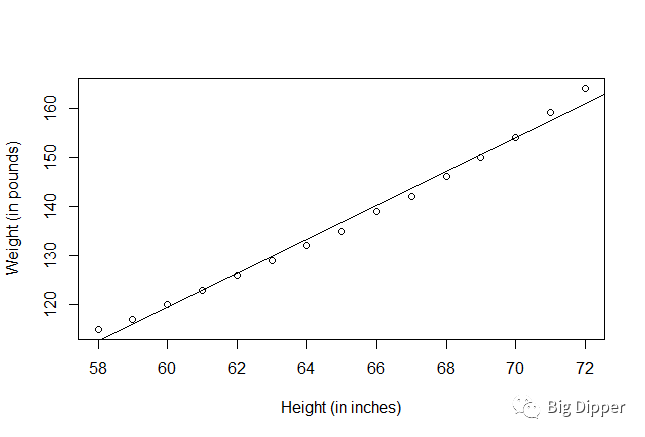
plot(women$height,women$weight,

     xlab="Height (in inches)",

     ylab="Weight (in pounds)")#生成观测，变量散点图

abline(fit)#给散点图加上拟合曲线

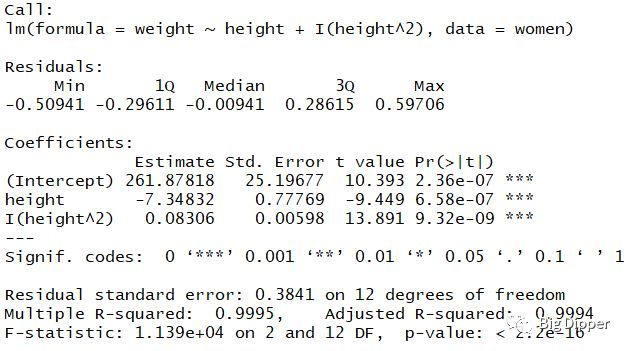
(2)多项式回归

fit2=lm(weight~height+I(height^2),data=women)#I(height^2)表示向预测等式添加一个平方项

summary(fit2)

plot(women$height,women$weight,

     xlab="Height (in inches)",

     ylab="Weight (in pounds)")

lines(women$height,fitted(fit2))

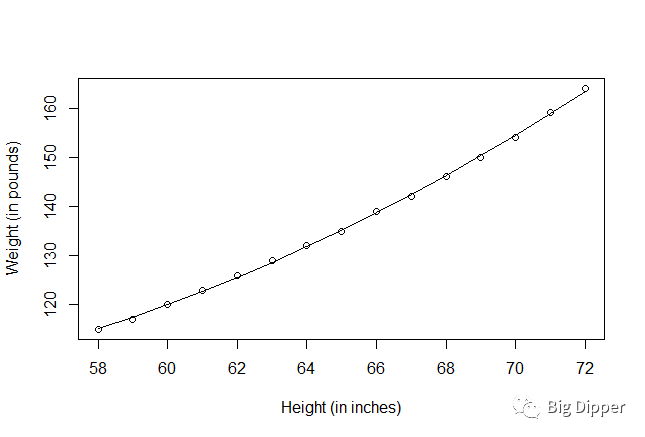
fit3=lm(weight~height+I(height^2)+I(height^3),data=women)

summary(fit3)

lines(women$height,fitted(fit3),col="red")

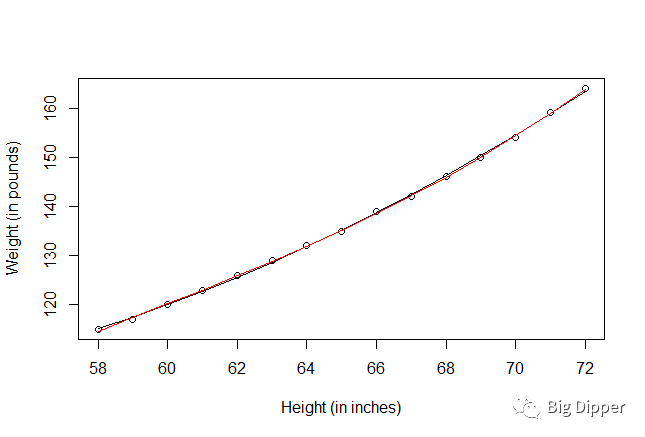
#使用car包的scatterplot()函数

install.packages("car")

library(car)

library(carData)

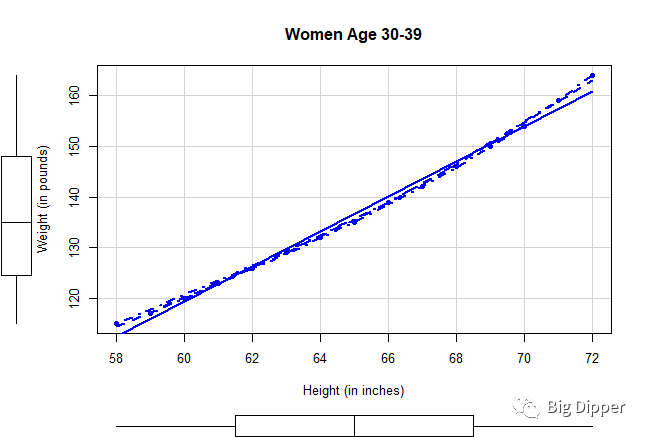
scatterplot(weight~height,data=women,

            spread=FALSE,smooth.args=list(lty=2),pch=19,

            main="Women Age 30-39",

            xlab="Height (in inches)",

            ylab="Weight (in pounds)")

#该函数提供了身高与体重的散点图，线性拟合曲线以及平滑拟合曲线(loess)，每个轴还展示了两个变量的箱线图。

(3)多元线性回归

states

cor(states)#检查一下各变量之间的相关性

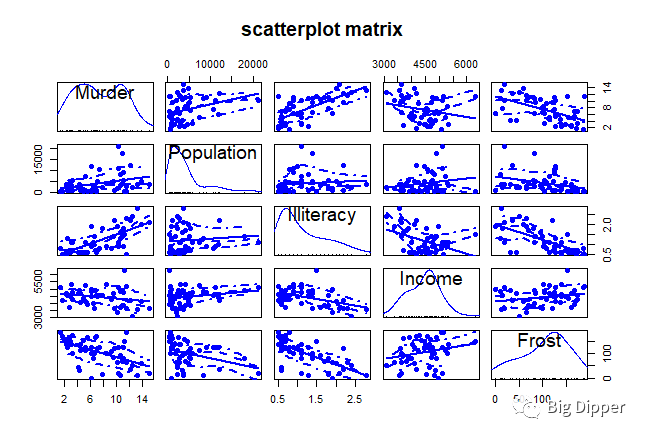
scatterplotMatrix(states,spread=FALSE,smooth.args=list(lty=2),pch=19,main="scatterplot matrix")

#非对角线位置绘制变量间的散点图，并添加平滑和线性回归图

#对角线区域绘制每个变量对应的密度图和轴须图

#使用lm函数进行没有交互项多元线性回归的拟合

states

fit=lm(Murder~Population+Illiteracy+Income+Frost,data=states)

summary(fit)

#使用lm函数进行有交互项多元线性回归的拟合

fit

summary(fit)

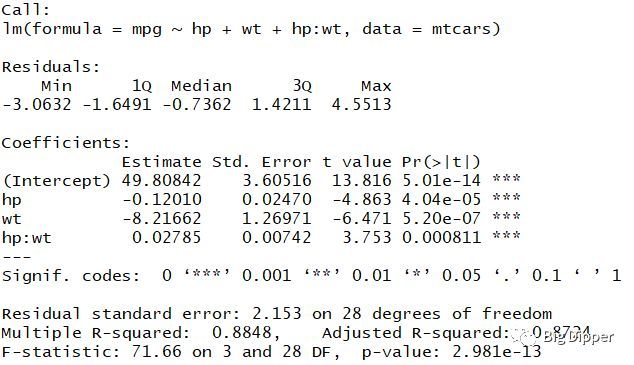
交互项也是显著的，说明相应变量与其中一个预测变量之间的关系依赖于另一个预测变量。

(4)回归诊断--常规方法

fit

par(mfrow=c(2,2))

plot(fit)

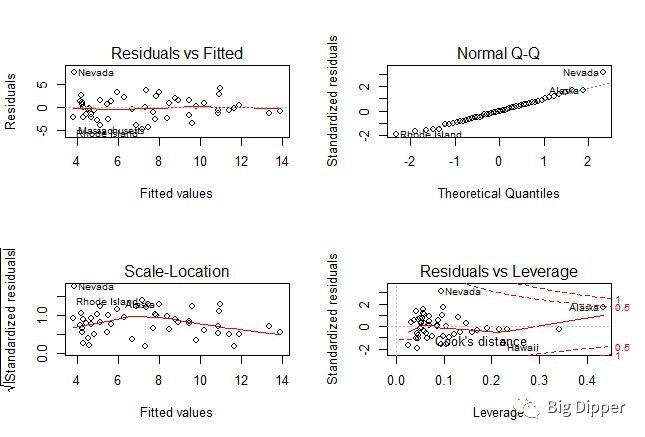
R vs F图：如果自变量和因变量线性相关，残差值和拟合值之间没有任何系统联系，如果是一条清楚的曲线，可能在暗示要在拟合的时候加上多次项

正态QQ图：当自变量的值固定时，因变量应该成正态分布，残差值也应该是一个均值为0的正态分布，如果满足假设，图上的点应该都落在一条45度的直线上

scale-location图:如果满足方差不变的假设，图中水平线周围的点应该随机分布

Residuals vs leverage图：鉴别离群点，高杠杆值点，强影响点。

加上多次项的拟合结果

fit2

par(mfrow=c(2,2))

plot(fit2)

13和15是强影响点，可以去除强影响点。

fit2

再对数据集state.x77进行试验

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit=lm(Murder~Population+Illiteracy+Income+Frost,data=states)

par(mfrow=c(2,2))

plot(fit)

(5)回归诊断--改进方法

library(car)

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit=lm(Murder~Population+Illiteracy+Income+Frost,data=states)

par(mfrow=c(1,1))

qqPlot(fit,labels=row.names(states),id.method="identify",simulate=TRUE,main="Q-Q Plot")

states["Nevada",]

fitted(fit)["Nevada"]

residuals(fit)["Nevada"]

rstudent(fit)["Nevada"]

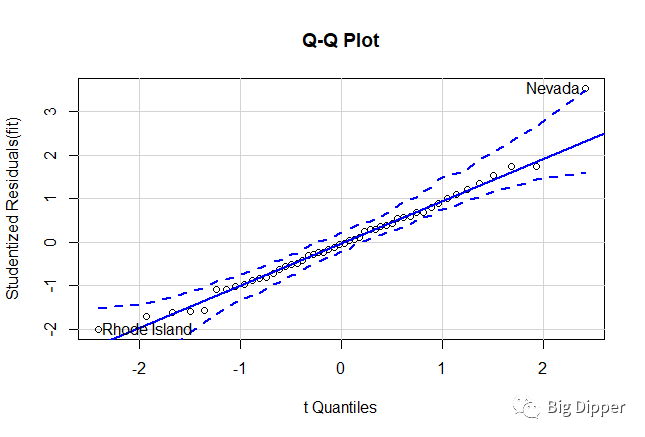
学生化残差

residplot

  z

  hist(z,breaks=nbreaks,freq=FALSE,

       xlab="Studentized Residual",

       main="Distribution of Errors")

  rug(jitter(z),col="brown")

 curve(dnorm(x,mean=mean(z),sd=sd(z)),add=TRUE,col="blue",lwd=2)

  lines(density(z)$x,density(z)$y,

        col="red",lwd=2,lty=2)

  legend("topright",

         legend=c("Normal Curve","Kernel Density Curve"),

         lty=1:2,col=c("blue","red"),cex=.8)

}

residplot(fit)

除了一个很明显的离群点，误差很好地服从了正态分布。

误差的独立性

durbinWatsonTest(fit)

crPlots(fit)

p值显著说明无自相关性，误差项之间独立。滞后项(lag=1)表明数据集中每个数据都是与其后一个数据进行比较。

通过成分残差图可以看因变量和自变量之间是否成非线性关系。

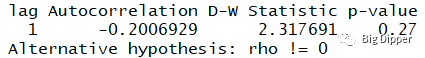
同方差性

ncvTest(fit)

spreadLevelPlot(fit)

分布水平图的点随机分布在直线的周围，如假设不正确，将看到曲线。

下图说明P值不显著，满足方差不变假设

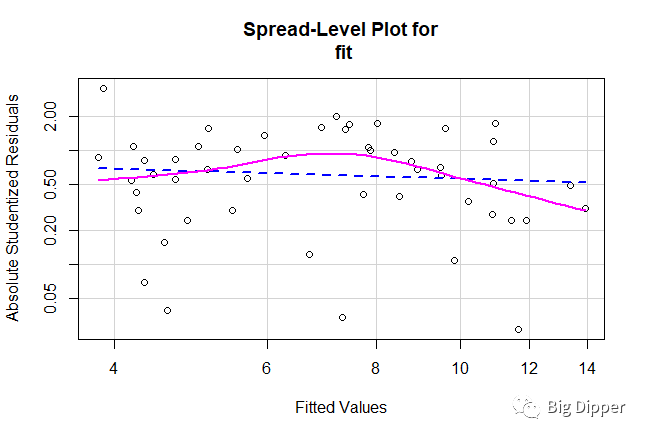
线性模型假设的综合验证

install.packages("gvlma")

library(gvlma)

gvmodel

summary(gvmodel)

下图表示P值都不显著，满足假设条件。

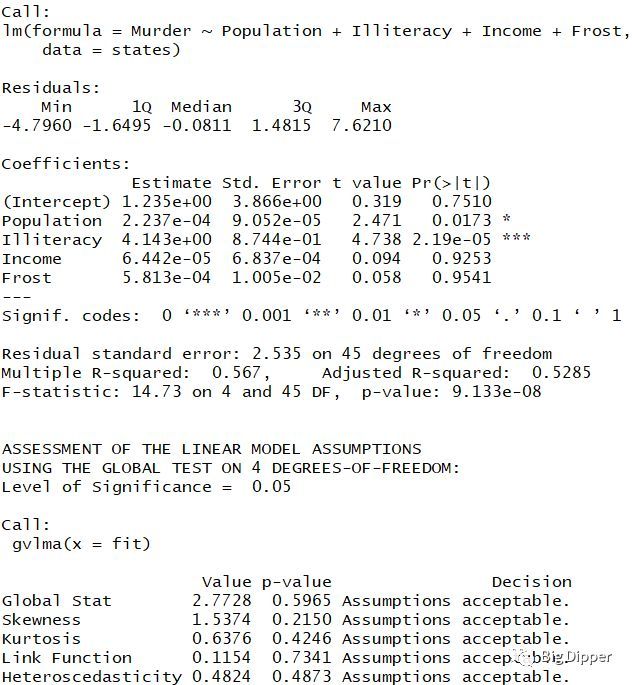
多重共线性

library(car)

vif(fit)

sqrt(vif(fit))#如果>2，表明存在多重共线性问题

(6)异常观测值

a.离群点：预测效果不佳的观测，有很大的或正或负的残差值。正代表模型低估了响应值，负代表模型高估了响应值

library(car)

outlierTest(fit)

返回值Nevada，P值小于0.05，判定为离群点。

       rstudent               unadjusted p-value     Bonferonni p

       Nevada 3.542929         0.00095088     0.047544

b.高杠杆点：与其他变量相关的离群点

hat.plot

  p

  n

  plot(hatvalues(fit),main="Index Plot of Hat Values")

  abline(h=c(2,3)*p/n,col="red",lty=2)

  identify(1:n,hatvalues(fit),names(hatvalues(fit)))

}

hat.plot(fit)

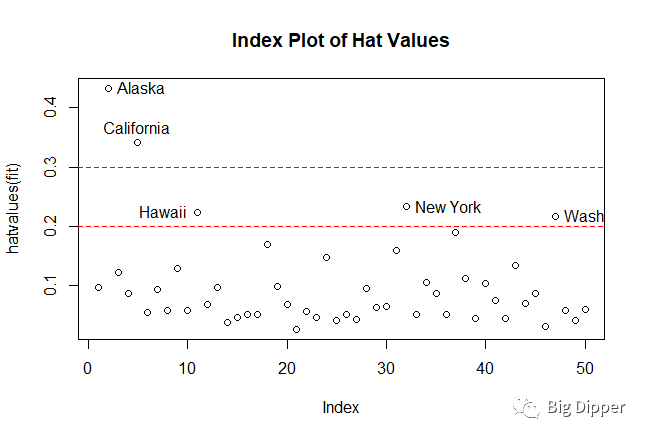
c.强影响点：模型估计参数值影响有些比例失衡的点，方法是测量Cook距离，可通过变量添加图得出。

一般来讲，Cook距离大于4/(n-k-1)，表明是强影响点。

n——样本量大小，K——预测变量数目

cutoff

plot(fit,which=4,cook,levels=cutoff)

abline(h=cutoff,lty=2,col="red")

下图中高于水平线的是强影响点

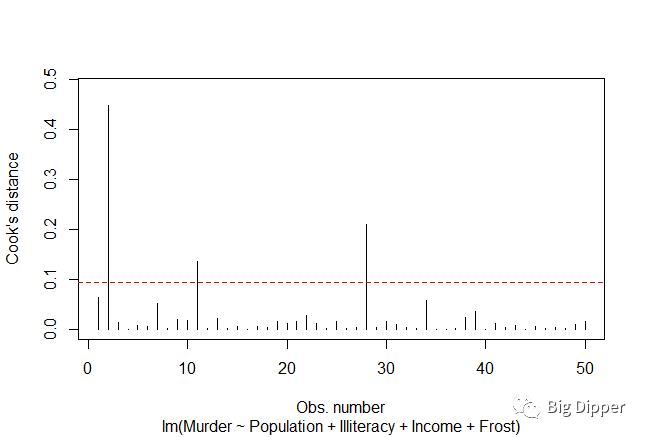
d.变量添加图：三种点都可以显现出来

library(car)

avPlots(fit,ask=FALSE,id.method="identify")

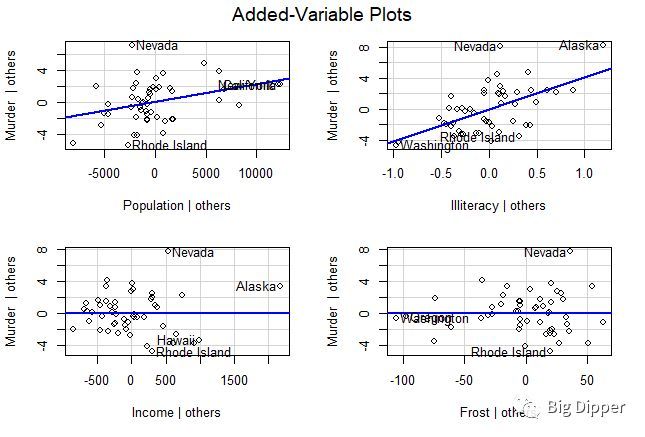
整合到一张图

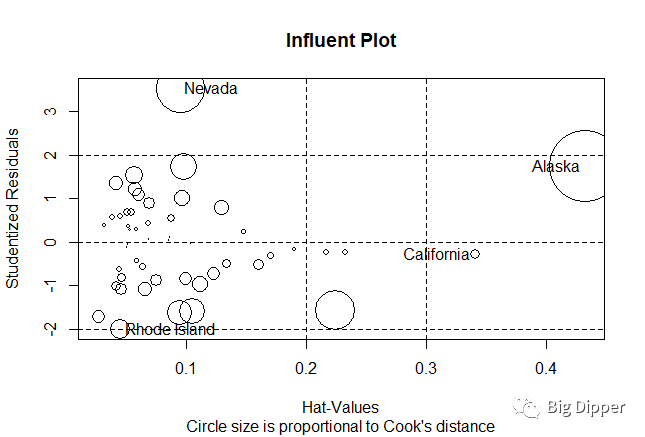
library(car)

influencePlot(fit,id.method="identify",main="Influent Plot",

              sub="Circle size is proportional to Cook's distance")

纵坐标超过正负2的被认为是离群点，水平轴超过0.2或0.3的被认为是高杠杆点，圆圈大的被认为是强影响点。

(7)处理违背回归假设的问题

a.删除变量：离群点和强影响点

b.变量变换：当模型违反正态假设时

library(car)

summary(powerTransform(states$Murder))

结果表明可以用Murder^0.6来正态化Murder，该函数使用极大似然法正态化变量

library(car)

boxTidwell(Murder~Population+Illiteracy,data=states)

           MLE of lambda  Score Statistic (z) Pr(>|z|)

Population   0.86939             -0.3228   0.7468

Illiteracy       1.35812              0.6194   0.5357

iterations =  19 

结果显示使用Population0.86939和Illiteracy1.35812可以大大改善线性关系。但对二者的记分检验又表明不会不需要变换。p值比较大。

c.增删变量：改变模型的变量数目可以影响变量的拟合优度——多重共线的变量要删掉

(8)选择最佳的回归模型

a.模型比较：

a1. anova()函数，需要模型嵌套

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit1=lm(Murder~Population+Illiteracy+Income+Frost,data=states)

fit2=lm(Murder~Population+Illiteracy,data=states)

anova(fit1,fit2)

anova将两个回归模型进行比较,p值(0.9939)不显著，所以不需要加到模型中。

a2. AIC(赤池信息准则)：考虑模型的统计拟合优度，AIC值小的要优先选择。

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit1=lm(Murder~Population+Illiteracy+Income+Frost,data=states)

fit2=lm(Murder~Population+Illiteracy,data=states)

AIC(fit1,fit2)

        df      AIC

fit1  6   241.6429

fit2  4   237.6565

根据AIC值选择fit2,不需要模型嵌套。

b.变量选择:

b1. 逐步回归法：模型每次增加(向前)或者删除(向后)一个变量，直到达到某个判停条件为止。

library(MASS)

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit=lm(Murder~Population+Illiteracy+Income+Frost,data=states)

stepAIC(fit,direction = "backward")

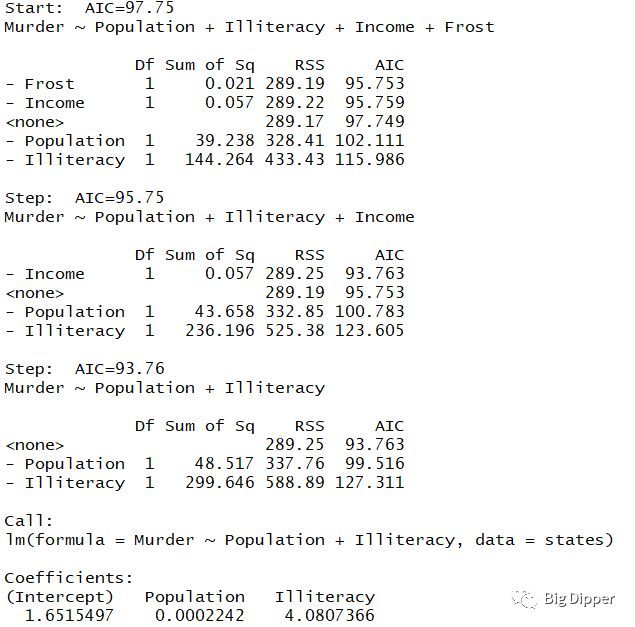
开始模型删除一个变量之后，AIC值降低，再删除一个变量之后，AIC值变低，最后剩下两个变量。弊端：不能找到最佳的

b2. 全子集回归法：所有可能的模型都会被检验。

install.packages("leaps")

library(leaps)

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

leaps=regsubsets(Murder~Population+Illiteracy+Income+Frost,data=states,nbest=4)

leaps

plot(leaps,scale="adjr2")

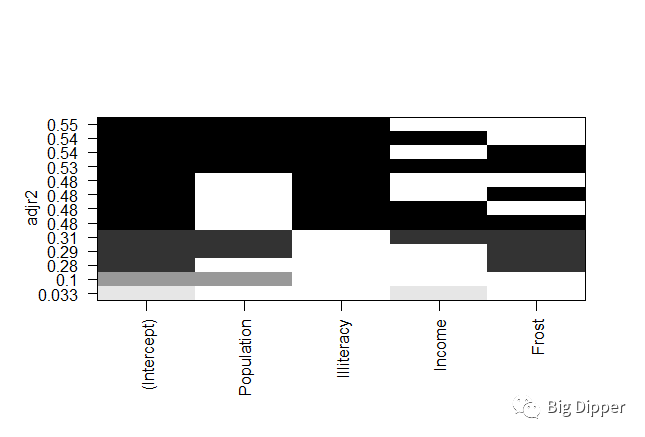
图中的0.33表示截距项与income变量模型调整R平方0.33，可以看出截距项和P和I的调整模型R平方和最大，模型最佳

or:

library(car)

subsets(leaps,statistic="cp",main="Cp Plot for All Subsets Regression")

abline(1,1,lty=2,col="red")

越好的模型离截距和斜率都为1的红线最近。

(9)深层次分析

a.交叉验证：最小二乘法的目的时预测误差(残差)平方和最小，响应变量解释度(R平方)最大化，交叉验证法可以评定该回归模型的泛化能力。

定义：将一定的数据挑选出来作为训练样本，其他的数据作为保留样本，现在训练样本中做回归，再在保留样本中做预测

install.packages("bootstrap")

library(bootstrap)

shrinkage

  require(bootstrap)

  theta.fit

    lsfit(x,y)

  }

  theta.predict

  x

  y

  results

  r2

  r2cv

  cat("Original R-square=",r2,"\n")

  cat(k,"Fold Cross-Validated R-square=",r2cv,"\n")

  cat("Change=",r2-r2cv,"\n")

}

states

fit

shrinkage(fit)

结果：

Original R-square= 0.5669502 

10 Fold Cross-Validated R-square= 0.4642092 

Change= 0.1027411 

验证后的R值更客观，验证前过于乐观,R值较大。

fit2

shrinkage(fit2)

验证前后R方变化不大，说明模型预测较为精确。

b.相对重要性：比较标准化回归系数，表示当其他预测变量不变时，该预测变量一个标准差的变化可yying引起响应值的变化。

在回归分析前，先将数据集用scale函数标准化为均值为0，标准差1的矩阵，再转化为数据框进行回归分析。

states=as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

zstates=as.data.frame(scale(states))

zfit=lm(Murder~Population+Illiteracy+Income+Frost,data=ztates)

coef(zfit)

结果：

  (Intercept)    Population    Illiteracy        Income         Frost 

-2.054026e-16  2.705095e-01  6.840496e-01  1.072372e-02  8.185407e-03 

结果显示：人口和文盲率对谋杀率的影响很大，而Frost的影响率很小。

c.相对权重法：将相对重要性看成是每个预测变量对R平方的贡献大小。

relweight

  R

  nvar

  rxx

  rxy

  svd

  evec

  ev

  delta

  lambda

  lambdasq

  beta

  rsquare

  rawwgt

  import

  import

  row.names(import)

  names(import)

  import

  dotchart(import$Weights,labels = row.names(import),

           xlab="% of R-Square",pch=19,

           main="Relative Importance of Predictor Variables",

           sub=paste("Total R-Square=",round(rsquare,digit=3))

  )

}

states

fit

relweight(fit,col="grey")

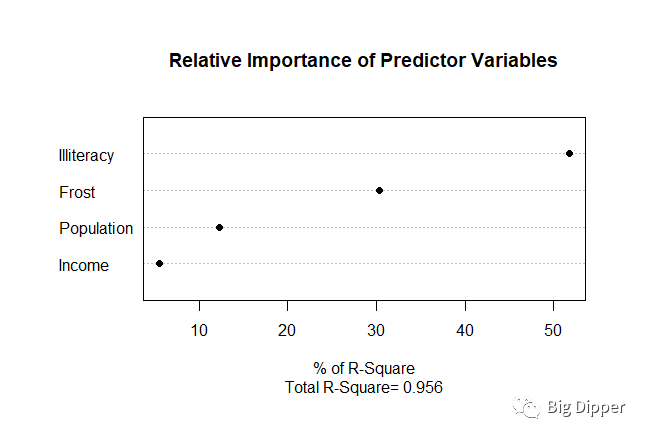
结果显示，文盲率对谋杀率的影响最大，其次是结冰率。