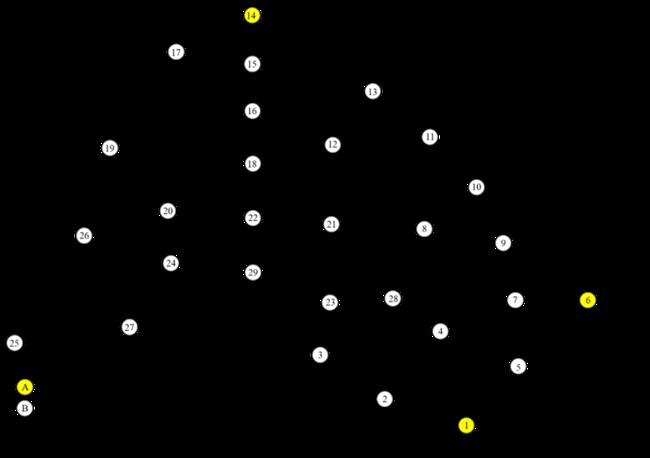
基于多目标优化模型的景区线路优化模型

多目标优化模型

在游线优化设计中考虑了拥挤度、满意度和走行时间三个指标，优化目标方程函数描述如公式

$$Min\{\sum _{i=1}^n{I}_c^i{x}_i\}(1)$$
$$Max\{\sum _{i=1}^n{I}_s^i{x}_i\}(2)$$
$$Min\{\sum _{i=1}^n{I}_t^i{x}_i\}(3)$$

式中，$I_c^i$为游线中第$i$个景点的拥挤度，$I_s^i$为游线中第$i$个景点的满意度，$I_t^i$为游线中从第$i-1$个景点到第$i$个景点之间的走行时间；$x_i=1$表示第$i$个景点在游线上；$x_i=0$表示第$i$个景点不在游线上；$n$为游线中包含的景点个数。
将景点拥挤度感知最低设为第一优化目标，将满意度最大设为第二优化目标，将景点间走行时间最小设为第三优化目标。多目标优化模型如下：

$$Minz=P_1(d_1^{+})+P_2(d_2^{-})+P_3(d_3^{+})(4)$$

s.t.
$$\sum _{i=1}^n{I}_c^i{x}_i+d_1^{-}-d_1^{+}=E_{max}(5)$$

$$\sum _{i=1}^n{I}_s^i{x}_i+d_2^{-}-d_2^{+}=E_{max1}(6)$$

$$\sum _{i=1}^n{I}_t^i{x}_i+d_1^{-}-d_1^{+}=E_{max2}(7)$$

$$T_{min}\le T\le T_{max}(8)$$

$$n_{min}\le n\le n_{max}(9)$$

$$x_i,d_k^{-},d_k^{+}\ge 0,k=1,2,3;(10)$$

式中：$P_1、P_2、P_3$ 为目标优先因子，$P_1$ 为第一优先因子，表示景点拥挤度最低， $P_2$为第二优先因子，表示景点满意度最高， $P_3$为第三优先分子，表示景点间走行时间最小； $E_{max}$为景点拥挤度最小值， $d_1^{-}$为负偏差变量，表示决策值未达到景点拥挤度最小的值部分， $d_1^{+}$为正偏差变量，表示决策值超过景点拥挤度最小值的部分； $E_{max1}$为景点满意度最大值， $d_2^{-}$为负偏差变量，表示决策值未达到景点满意度最大值的部分， $d_2^{+}$为正偏差变量，表示决策值超过景点满意度最大值的部分； $E_{max2}$为景点间走行时间最小值， $d_3^{-}$为负偏差变量，表示决策值未达到景点间走行时间最小值的部分， $d_3^{+}$为正偏差变量，表示决策值超过景点间走行时间最小值的部分。
公式（8）代表为游客总游览时间约束，公式（9）代表为游览景点个数约束。$T$ 为总游览时间（总游览时间=景点停留时间+景点间走行时间）， $T_{min}$为总游览时间最小值， $T_{max}$为总游览时间最大值； $n$为景点个数，n_{min}$ 为游线最少景点个数， $n_{max}$为游线最多景点个数。

多目标优化模型求解

采用目标规划层次算法求解多目标优化模型，在严格满足刚性约束的条件下，依据实际要求，允许多个目标约束出现偏差，依据目标约束的优先级逐层优化。
第一步：对目标函数中的$P_1$ 层进行优化

$$Min{Z}_1=d_1^{+}(11)$$

第二步：对目标函数中的$P_2$ 层进行优化

$$Min{Z}_2=d_2^{+}(12)$$

第三步：对目标函数中的$P_3$ 层进行优化

$$Min{Z}_3=d_3^{+}(13)$$

定义和计算第$j$条旅游线路的拥挤度偏差指数${\delta }_{cj}$、满意度偏差指数${\delta }_{sj}$和景点间走行时间偏差指数${\delta }_{tj}$，利用偏差分析法，比较三个偏差指数和相应偏差值的标准偏差，筛选出旅游线路的初步可接受解，以拥挤度偏差指数为例：

$${\delta }_{cj}=\frac{d_1^{+}}{E_{max}}(14)$$

$${\eta }_c=\sqrt{\frac{{\sum }_{j=1}^N({\delta }_{cj}-{\overline{\delta }}_{cj}{)}^2}{N}}(15)$$

当 ${\delta }_{cj}=0$ 时，拥挤度达到预期最低值，为理想值；
当 $0\le {\delta }_{cj}\le {\eta }_c$时，拥挤度值为可接受解， ${\eta }_c$为拥挤度偏差值的标准偏差， $N$为线路条数。
当${\delta }_{cj}>{\eta }_c$时，游客对所游览景点的拥挤度较高，需要重新进行游线设计。
第四步：线路优度评价
在利用多目标优化模型求解出可接受解集的基础上，对解集中的线路进行优度评价和排序。基于粒子群算法求解最优解的思路，提出一种改进粒子群适应度的函数，如公式16所示，根据函数计算出的优度值对线路进行评价排序，优度值越大，说明线路越趋于最优解。

$$S_j=100\times \{1-[w_c(\frac{f_c-f_{c,min}}{f_{c,max}-f_{c,min}})+w_s(\frac{f_s-f_{s,min}}{f_{s,max}-f_{s,min}})+w_t(\frac{f_t-f_{t,min}}{f_{t,max}-f_{t,min}})]\}(16)$$

式中，$w_c$ 、$w_s$ 、$w_t$ 分别为线路拥挤度、线路满意度、景点间走行时间的惯性权重；$f_{c,min}$ 、$f_{c,max}$ 分别为所有线路总体拥挤度的最大值和最小值；$f_{s,min}$ 、$f_{s,max}$ 分别为所有线路总体满意度的最大值和最小值；$f_{t,min}$ 、$f_{t,max}$ 分别为所有线路景点间走行时间的最大值和最小值；$f_c$ 、$f_s$ 、$f_t$ 分别为第 条线路的总体拥挤度、总体满意度和景点间走行时间；$S_j$为第$j$ 条线路的优度值，优度值越大，线路越趋于最优解。

案例求解

景点14→6线路优化

各项优化指标（拥挤度、满意度、景点间走行时间) 的偏差值和相应偏差值的标准偏差（${\delta }_{cj}$ 、${\delta }_{sj}$ 、${\delta }_{tj}$ 、${\eta }_c$ 、${\eta }_s$ 、${\eta }_t$ ）
$w_c=0.28$、$w_s=0.36$ 、$w_t=0.36$
优化线路（线路编号、景点及顺序、景点总拥挤度、景点总满意度、景点间走行时间、优度值）

点击matlab代码运行，显示出经3层优化后，所有可选的路径信息。路径信息包括（线路编号、景点及顺序、景点总拥挤度、景点总满意度、景点间走行时间、优度值），下图为其中一条可行路径。

具体MATLAB代码参考
多目标优化模型求解matlab实现