单目视觉(4):SFM之相机模型(二)
SFM之相机标定(二)
- SFM之相机标定(二)
- 成像模型(Imaging Model)
- 坐标系统(Coordinate System )
- 畸变校正
- 相机标定(Camera Calibration)
- 张正友标定法
- 标定图像获取
- Matlab标定源码分析
- OpenCV 标定源码分析
- 参考资料(Reference)
成像模型(Imaging Model)
现代一句城乡模型大致可以分为小孔成像相机和透镜成像相机。 以下分别是两种成像模型的光路图。
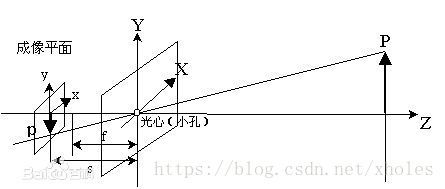

在透镜成像模型中,我们依据物理学知识,已知透镜焦距 f f ,像距m m ,物距 n n ,可以得到:
而在小孔成像模型中,我们将像的位置设置在“焦距” f f 上,因此有:
一般地,由于物距远大于焦距,即 n>>f,所以 m≈f,此时可以用小孔模型代替透镜模型。
坐标系统(Coordinate System )
在相机成像模型中,存在多个坐标系,分别有:像素坐标系,图像坐标系,相机坐标系以及世界坐标系。

为方面分析,如果将像平面转移至物体和相机之间,那么加上定义的三个坐标系,可以得到如下图所示的结构:
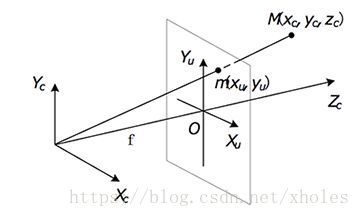
结合成像关系,可以得到相机坐标系和图像坐标系的关系:
相片是由感光元件的作用而来,每个感光元件都有固定的尺寸大小( dx,dy d x , d y ),一个感光元件代表图像中的一个像素。因此图像坐标系和像素坐标系有如下关系:
而世界坐标系与相机坐标系的关系和如何选取世界坐标系有关,通常两个坐标系的变换可以通过旋转和平移来实现变换(也就是常说的刚体变换):
总结所的坐标系关系,可以得到像素坐标系和世界坐标系的关系(实际情况情况可能比这还复杂):
即:
其中, s s 为尺度因子, K K 为相机内参矩阵, R R 为旋转矩阵,T T 为评议矩阵。
畸变校正
在成像时,理论上直线应该投影成为直线。但实际在透镜成像过程中,并非如此,这就是所谓的光学畸变。这种现象在远离像中心的部分畸变程度越大。畸变可以将其分为切向畸变和径向畸变。
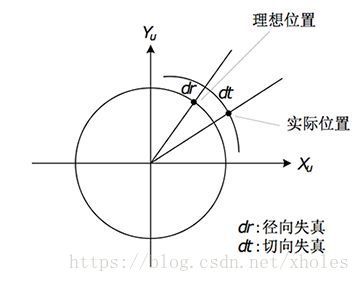
理想的畸变模型下,理想的像素坐标与畸变像素的坐标关系如下:
径向畸变包括枕型畸变和桶型畸变,这主要是由于透镜的不太完美而造成的。其畸变模型可以表示为:
切向畸变包括离心畸变和薄透镜畸变等。薄透镜畸变主要发生在透镜组之中,而薄透镜畸变主要由于透镜倾斜而引发。其畸变模型可以表示为:
那么,可以推导出理想坐标和实际坐标的关系为:
相机标定(Camera Calibration)
相机的标定主要的通过实验的方法来确定前述的一些参数,包括内参数矩阵,外参数矩阵,畸变矩阵等。
- 外参数矩阵:告诉你现实世界点(世界坐标)是怎样经过旋转和平移,然后落到另一个现实世界点(摄像机坐标)上。
- 内参数矩阵:告诉你上述那个点在1的基础上,如何继续经过摄像机的镜头、并通过针孔成像和电子转化而成为像素点。
畸变矩阵。告诉你为什么上面那个像素点并没有落在理论计算该落在的位置上,还产生了一定的偏移和变形。
张正友标定法
设三维世界坐标的点为 [xw,yw,zw,1]T [ x w , y w , z w , 1 ] T ,二维相机平面像素坐标为 [X,Y,1]T [ X , Y , 1 ] T ,所以标定用的棋盘格平面到图像平面的单应性关系为:
s⎡⎣⎢XY1⎤⎦⎥=K[R,T]⎡⎣⎢⎢⎢xwywzw1⎤⎦⎥⎥⎥ s [ X Y 1 ] = K [ R , T ] [ x w y w z w 1 ]
令其中的 K K 为:
K=⎡⎣⎢α00γβ0X0Y01⎤⎦⎥ K = [ α γ X 0 0 β Y 0 0 0 1 ]
当世界坐标系放在标定棋盘上时,此时 zw=0 z w = 0 ,那么代入公式可以得到:
s⎡⎣⎢XY1⎤⎦⎥=K[r1r2r3t]⎡⎣⎢⎢⎢xwyw01⎤⎦⎥⎥⎥=K[r1r2t]⎡⎣⎢xwyw1⎤⎦⎥=H⎡⎣⎢xwyw1⎤⎦⎥ s [ X Y 1 ] = K [ r 1 r 2 r 3 t ] [ x w y w 0 1 ] = K [ r 1 r 2 t ] [ x w y w 1 ] = H [ x w y w 1 ]
即,称 H H 为单应性矩阵:
s⎡⎣⎢uv1⎤⎦⎥=H⎡⎣⎢XY1⎤⎦⎥H=[h1 h2 h3]=λK[r1 r2 t] s [ u v 1 ] = H [ X Y 1 ] H = [ h 1 h 2 h 3 ] = λ K [ r 1 r 2 t ]
H是一个齐次矩阵,有一个元素为1,所以存在8个未知数,因此至少需要8个方程才能解得方程。每一个点对可以提供两个方程,因此至少需要四个对应的点对才能够得到一个解。
标定图像获取
1。图片放置的位置要能覆盖整个测量视场, 在相机所能拍摄到的各个区域尽可能的获取图片。
2。图片的数量通常在15~25张之间,图像数量太少,容易导致标定参数不准确,但是太多容易影响标定时间。
3。标定板的成像尺寸应大致占整幅画面的1/4
4。标定板成像应该清晰,也就是图像质量要尽量好,不要有过曝、虚影、光照不均等情况
5。标定过程,相机的光圈、焦距不能发生改变,改变需要重新标定。
Matlab标定源码分析
主程序如下:
function calibration()
numImages = 5;
files = cell(1, 5);
for i = 1:numImages
files{i} = fullfile('C:\\path\\to\\pics\\', sprintf('IMG_%d.jpg', i));
end
[imagePoints, boardSize] = detectCheckerboardPoints(files);\\检测棋盘格上的点
squareSize = 25; % in millimeters 设置棋盘格各自大小尺寸
worldPoints = generateCheckerboardPoints(boardSize, squareSize);\\生成点的世界坐标
cameraParams = estimateCameraParameters(imagePoints, worldPoints);\\估计出参数
角点检测的核心函数如下:
function [points, boardSize] = detectCheckerboard(I, sigma, peakThreshold)
%#codegen
[cxy, c45, Ix, Iy] = ...
vision.internal.calibration.checkerboard.secondDerivCornerMetric(I, sigma);
[Ix2, Iy2, Ixy] = computeJacobianEntries(Ix, Iy);
points0 = vision.internal.calibration.checkerboard.find_peaks(cxy, peakThreshold);
scores0 = cxy(sub2ind(size(cxy), points0(:, 2), points0(:, 1)));
board0 = growCheckerboard(points0, scores0, Ix2, Iy2, Ixy, 0);
points45 = vision.internal.calibration.checkerboard.find_peaks(c45, peakThreshold);
scores45 = c45(sub2ind(size(c45), points45(:, 2), points45(:, 1)));
board45 = growCheckerboard(points45, scores45, Ix2, Iy2, Ixy, pi/4);
points = [];
boardSize = [0 0];
if board0.isValid && board0.Energy < board45.Energy
board0 = orient(board0, I);
[points, boardSize] = toPoints(board0);
points = vision.internal.calibration.checkerboard.subPixelLocation(cxy, points);
elseif board45.isValid
board45 = orient(board45, I);
[points, boardSize] = toPoints(board45);
points = vision.internal.calibration.checkerboard.subPixelLocation(c45, points);
end
end
世界坐标生成函数:
function worldPoints = generateCheckerboardPoints(boardSize, squareSize)
% 生成标定板上所检测的角点的世界坐标
% 返回一个 M x 2 矩阵,包含格子角点的x-y 坐标。角点 (0,0)对应板上左上方格的右下角点,
% 即该点为定义的世界坐标原点。boardSize 是一个含有2个元素的向量,指明了格子的数量和排布信息。返回的点
% 个数M = (boardSize(1)-1) * (boardSize(2)-1). squareSize 是一个表明格子尺寸(实际大小)的标量
%
%
% % offset the points to place the first point at lower-right corner of the
% % first square.
checkInputs(boardSize, squareSize);
boardSize = double(boardSize) - 1;
worldPoints = zeros(boardSize(1) * boardSize(2), 2);
k = 1;
for j = 0:boardSize(2)-1
for i = 0:boardSize(1)-1
worldPoints(k,1) = j * squareSize;
worldPoints(k,2) = i * squareSize;
k = k + 1;
end
end矩阵计算:
%--------------------------------------------------------------------------
function H = computeHomography(imagePoints, worldPoints)
% Compute projective transformation from worldPoints to imagePoints
H = fitgeotrans(worldPoints, imagePoints, 'projective');
H = (H.T)';
H = H / H(3,3);
%--------------------------------------------------------------------------
function V = computeV(homographies)
% Vb = 0
numImages = size(homographies, 3);
V = zeros(2 * numImages, 6);
for i = 1:numImages
H = homographies(:, :, i)';
V(i*2-1,:) = computeLittleV(H, 1, 2);
V(i*2, :) = computeLittleV(H, 1, 1) - computeLittleV(H, 2, 2);
end
%--------------------------------------------------------------------------
function v = computeLittleV(H, i, j)
v = [H(i,1)*H(j,1), H(i,1)*H(j,2)+H(i,2)*H(j,1), H(i,2)*H(j,2),...
H(i,3)*H(j,1)+H(i,1)*H(j,3), H(i,3)*H(j,2)+H(i,2)*H(j,3), H(i,3)*H(j,3)];
%--------------------------------------------------------------------------
function B = computeB(V)
% lambda * B = inv(A)' * inv(A), where A is the intrinsic matrix
[~, ~, U] = svd(V);
b = U(:, end);
% b = [B11, B12, B22, B13, B23, B33]
B = [b(1), b(2), b(4); b(2), b(3), b(5); b(4), b(5), b(6)];
%--------------------------------------------------------------------------
function A = computeIntrinsics(B)
% Compute the intrinsic matrix
cy = (B(1,2)*B(1,3) - B(1,1)*B(2,3)) / (B(1,1)*B(2,2)-B(1,2)^2);
lambda = B(3,3) - (B(1,3)^2 + cy * (B(1,2)*B(1,3) - B(1,1)*B(2,3))) / B(1,1);
fx = sqrt(lambda / B(1,1));
fy = sqrt(lambda * B(1,1) / (B(1,1) * B(2,2) - B(1,2)^2));
skew = -B(1,2) * fx^2 * fy / lambda;
cx = skew * cy / fx - B(1,3) * fx^2 / lambda;
A = vision.internal.calibration.constructIntrinsicMatrix(fx, fy, cx, cy, skew);
if ~isreal(A)
error(message('vision:calibrate:complexCameraMatrix'));
end
function [rotationVectors, translationVectors] = ...
computeExtrinsics(A, homographies)
% Compute translation and rotation vectors for all images
numImages = size(homographies, 3);
rotationVectors = zeros(3, numImages);
translationVectors = zeros(3, numImages);
Ainv = inv(A);
for i = 1:numImages;
H = homographies(:, :, i);
h1 = H(:, 1);
h2 = H(:, 2);
h3 = H(:, 3);
lambda = 1 / norm(Ainv * h1); %#ok
% 3D rotation matrix
r1 = lambda * Ainv * h1; %#ok
r2 = lambda * Ainv * h2; %#ok
r3 = cross(r1, r2);
R = [r1,r2,r3];
rotationVectors(:, i) = vision.internal.calibration.rodriguesMatrixToVector(R);
% translation vector
t = lambda * Ainv * h3; %#ok
translationVectors(:, i) = t;
end
rotationVectors = rotationVectors';
translationVectors = translationVectors';
OpenCV 标定源码分析
opencv标定相机的过程如下:
1. 准备标定图片
2. 对每一张标定图片,提取角点信息
3. 对每一张标定图片,进一步提取亚像素角点信息
4. 在棋盘标定图上绘制找到的内角点(非必须,仅为了显示)
5. 相机标定
6. 对标定结果进行评价
7. 查看标定效果——利用标定结果对棋盘图进行矫正
角点提取
CV_EXPORTS_W bool findChessboardCorners( InputArray image, Size patternSize,
OutputArray corners,
int flags = CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE );参数Image,传入拍摄的棋盘图Mat图像,必须是8位的灰度或者彩色图像;
参数patternSize,每个棋盘图上内角点的行列数,一般情况下,行列数不要相同,便于后续标定程序识别标定板的方向;
参数corners,用于存储检测到的内角点图像坐标位置,一般用元素是Point2f的向量来表示:vector;
参数flage:用于定义棋盘图上内角点查找的不同处理方式,有默认值。
角点亚像素化
为了提高标定精度,需要在初步提取的角点信息上进一步提取亚像素信息,降低相机标定偏差,常用的方法是cornerSubPix,另一个方法是使用find4QuadCornerSubpix函数。
//! adjusts the corner locations with sub-pixel accuracy to maximize the certain cornerness criteria
CV_EXPORTS_W void cornerSubPix( InputArray image, InputOutputArray corners,
Size winSize, Size zeroZone,
TermCriteria criteria ); 参数image,输入的Mat矩阵,最好是8位灰度图像,检测效率更高;
参数corners,初始的角点坐标向量,同时作为亚像素坐标位置的输出,所以需要是浮点型数据,一般用元素是Pointf2f/Point2d的向量来表示:vector
//! finds subpixel-accurate positions of the chessboard corners
CV_EXPORTS bool find4QuadCornerSubpix(InputArray img, InputOutputArray corners, Size region_size); 参数img,输入的Mat矩阵,最好是8位灰度图像,检测效率更高;
参数corners,初始的角点坐标向量,同时作为亚像素坐标位置的输出,所以需要是浮点型数据,一般用元素是Pointf2f/Point2d的向量来表示:vector;
参数region_size,角点搜索窗口的尺寸;
相机标定
获取到棋盘标定图的内角点图像坐标和相应的世界坐标后,可以使用calibrateCamera函数计算相机内参和外参系数。标定的结果是生成相机的内参矩阵cameraMatrix、相机的5个畸变系数distCoeffs,另外每张图像都会生成属于自己的平移向量和旋转向量。
//! finds intrinsic and extrinsic camera parameters from several fews of a known calibration pattern.
CV_EXPORTS_W double calibrateCamera( InputArrayOfArrays objectPoints,
InputArrayOfArrays imagePoints,
Size imageSize,
CV_OUT InputOutputArray cameraMatrix,
CV_OUT InputOutputArray distCoeffs,
OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs,
int flags=0, TermCriteria criteria = TermCriteria(
TermCriteria::COUNT+TermCriteria::EPS, 30, DBL_EPSILON) );
参数objectPoints,为世界坐标系中的三维点。在使用时,应该输入一个三维坐标点的向量的向量,即vector。需要依据棋盘上单个黑白矩阵的大小,计算出(初始化)每一个内角点的世界坐标。
参数imagePoints,为每一个内角点对应的图像坐标点。和objectPoints一样,应该输入vector形式的变量;
参数imageSize,为图像的像素尺寸大小,在计算相机的内参和畸变矩阵时需要使用到该参数;
参数cameraMatrix为相机的内参矩阵, 输入一个Mat cameraMatrix即可 ;
参数istCoeffs为畸变矩阵, 输入一个Mat distCoeffs 即可;
参数rvecs为旋转向量;应该输入一个Mat类型的vector,即vector;
参数tvecs为位移向量,和rvecs一样,应该为vector;
参数flags为标定时所采用的算法。有如下几个参数:
CV_CALIB_USE_INTRINSIC_GUESS:使用该参数时,在cameraMatrix矩阵中应该有fx,fy,u0,v0的估计值。否则的话,将初始化(u0,v0)图像的中心点,使用最小二乘估算出fx,fy。CV_CALIB_FIX_PRINCIPAL_POINT:在进行优化时会固定光轴点。当CV_CALIB_USE_INTRINSIC_GUESS参数被设置,光轴点将保持在中心或者某个输入的值。CV_CALIB_FIX_ASPECT_RATIO:固定fx/fy的比值,只将fy作为可变量,进行优化计算。当CV_CALIB_USE_INTRINSIC_GUESS没有被设置,fx和fy将会被忽略。只有fx/fy的比值在计算中会被用到。CV_CALIB_ZERO_TANGENT_DIST:设定切向畸变参数(p1,p2)为零。CV_CALIB_FIX_K1,…,CV_CALIB_FIX_K6:对应的径向畸变在优化中保持不变。CV_CALIB_RATIONAL_MODEL:计算k4,k5,k6三个畸变参数。如果没有设置,则只计算其它5个畸变参数。
参数criteria是最优迭代终止条件设定。
参考资料(Reference)
[1] OpenCV实现SfM(一): 相机模型
[2] 相机的那些事儿 (二)成像模型
[3]相机标定(Camera calibration)原理、步骤
[4] 机器视觉的相机标定到底是什么?
[5] 张正友相机标定Opencv实现以及标定流程&&标定结果评价&&图像矫正流程解析(附标定程序和棋盘图)
[6] 张正友标定算法原理详解