gtsam官方教程学习(doc_gtsam.pdf)
一、创建因子图初始化并优化待求解变量

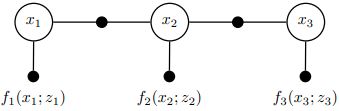
1.使用FactorGraph(NonlinearFactorGraph)类构建因子图模型,不提供求解方案(求解变量的方法以及优化器)。
1// 创建一个空的非线性因子图
2 NonlinearFactorGraph graph;
3
4 // 在位姿1上添加高斯位姿先验
5 Pose2 priorMean(0.0, 0.0, 0.0); // 设置先验位姿
6 noiseModel::Diagonal::shared_ptr priorNoise =
7 noiseModel::Diagonal::Sigmas(Vector3(0.3, 0.3, 0.1)); // 通过对角线元素配置先验的协方差矩阵,此处相当于(x,y,θ)上的标准差为(0.3m, 0.3m, 0.1rad)
8 graph.addPrior(1, priorMean, priorNoise); // 将先验因子添加到因子图中,第一个参数为变量标记,第二个参数为先验位姿,第三个参数为噪声协方差矩阵
9
10 // 添加两个里程计因子
11 Pose2 odometry(2.0, 0.0, 0.0); // 设置帧间里程计信息
12 noiseModel::Diagonal::shared_ptr odometryNoise =
13 noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1)); // 设置里程计观测的协方差矩阵,单位为m和rad
14 graph.add(BetweenFactor<Pose2>(1, 2, odometry, odometryNoise)); // 通过帧间里程计信息和噪声协方差矩阵配置1,2之间的里程计约束因子
15 graph.add(BetweenFactor<Pose2>(2, 3, odometry, odometryNoise)); // 同上
16 // 回环因子的添加方式和里程计因子相同,因为其表达的观测都是相对于两个变量,且观测信息为两个变量的帧间坐标变换
17 // 如在第2个位姿和第5个位姿之间添加回环因子
18 // noiseModel::Diagonal::shared_ptr model = noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
19 // graph.add(BetweenFactor(5, 2, Pose2(2, 0, M_PI_2), model));
2.使用Values类来对变量进行初始化。
1 // 实例化估计变量的变量集合并对变量进行初始化
2 Values initial;
3 initial.insert(1, Pose2(0.5, 0.0, 0.2)); // 为变量添加初值(变量符号和因子图中一致)
4 initial.insert(2, Pose2(2.3, 0.1, -0.2));
5 initial.insert(3, Pose2(4.1, 0.1, 0.1));
3.再根据构建的因子图和变量初始值用LM优化器进行优化求解。
7 // 使用LM优化器,根据因子图和变量集合对变量进行优化
8 Values result = LevenbergMarquardtOptimizer(graph, initial).optimize();
4.可通过marginals.marginalCovariance(变量代号)得到变量优化并边缘化后变量各自的噪声协方差矩阵。
1 // 求解各变量边缘化后的协方差矩阵
2 cout.precision(2);
3 Marginals marginals(graph, result);
4 cout << "x1 covariance:\n" << marginals.marginalCovariance(1) << endl;
5 cout << "x2 covariance:\n" << marginals.marginalCovariance(2) << endl;
6 cout << "x3 covariance:\n" << marginals.marginalCovariance(3) << endl;
二、创建并使用新的因子(以一元因子为例)
1.定义新的因子
通过NoiseModelFactor1定义新的一元因子,该模板类可实现与高斯噪声模型似然的一个观测对应的一元因子,其中T为一元因子所对应变量的类型。
此类因子形式如下,具有高斯噪声分布的形式。

需要针对新因子定义一下几个信息:
(1)有关传感器观测值的私有成员变量。
(2)有关因子初始化的构造函数。
(3)用于计算评估误差的误差函数,功能包括:返回变量和观测值之间的残差信息、计算用于非线性优化的雅克比矩阵。
以定义一元GPS因子为例
(1)定义GPS的x,y向测量值mx_, my_私有成员变量。
(2)定义GPS因子的构造函数,在使用时通过该函数实例化因子。用给定的x,y值初始化mx_, my_观测值,并给定与该因子连接的变量代号j以及观测的噪声协方差矩阵model。
(3)定义用于计算评估误差的函数evaluateError:
第14行给出了残差信息的计算方法:使用变量值减去观测值
![]()
第10-13行给出了雅克比矩阵的计算方法。为将该因子用于非线性优化,当给了参数H(雅克比矩阵存储位置)时,计算h(q)在当前状态q处进行线性化得到的雅克比矩阵。(具体数学计算本人并不理解)
1 class UnaryFactor: public NoiseModelFactor1<Pose2> { // 表明该GPS类继承于模板类NoiseModelFactor1,并且变量为Pose2类型
2 double mx_, my_; // GPS的x,y向测量值
3
4 public:
5 UnaryFactor(Key j, double x, double y, const SharedNoiseModel& model):
6 NoiseModelFactor1<Pose2>(model, j), mx_(x), my_(y) {} // 定义GPS因子的构造函数
7
8 Vector evaluateError(c o n s t Pose2& q, boost::optional<Matrix&> H = boost::none) const
9 {
10 const Rot2& R = q.rotation();
11 if (H) (*H) = (gtsam::Matrix(2, 3) <<
12 R.c(), -R.s(), 0.0,
13 R.s(), R.c(), 0.0).finished();
14 return (Vector(2) << q.x() - mx_, q.y() - my_).finished();
15 }
16 };
1 // 添加GPS因子到因子图中
2 noiseModel::Diagonal::shared_ptr unaryNoise =
3 noiseModel::Diagonal::Sigmas(Vector2(0.1, 0.1)); // x,y方向上标准差均为10cm
4 graph.add(boost::make_shared<UnaryFactor>(1, 0.0, 0.0, unaryNoise)); // 将GPS因子添加到相应的变量节点
5 graph.add(boost::make_shared<UnaryFactor>(2, 2.0, 0.0, unaryNoise));
6 graph.add(boost::make_shared<UnaryFactor>(3, 4.0, 0.0, unaryNoise));
3.初始化变量并根据因子图进行优化
变量初始化和优化操作和基本因子相同。
三、使用iSAM进行优化
iSAM会在优化过程中,根据设定好的处理次数间隔,对变量进行重新线性化和重新排序。在iSAM2中,处理间隔不需要认为规定,它会自动决定何时以及那些变量需要重新线性化及排序。
使用iSAM进行优化的例子
假设已经初始化了变量集合initial_x以及观测集合z,则通过relinearizeInterval参数配置并实例化iSAM优化器,再通过for循环将各个因子添加到因子图中并初始化待优化变量,即可使用isam.update()对变量进行优化,在执行过程中优化器会根据配置重新对变量进行线性化。
1 int relinearizeInterval = 3;
2 NonlinearISAM isam(relinearizeInterval);
3
4 // ... first frame initialization omitted ...
5
6 // Loop over the different poses, adding the observations to iSAM
7 for (size_t i = 1; i < poses.size(); ++i) {
8
9 // Add factors for each landmark observation
10 NonlinearFactorGraph graph;
11 for (size_t j = 0; j < points.size(); ++j) {
12 graph.add(
13 GenericProjectionFactor<Pose3, Point3, Cal3_S2>
14 (z[i][j], noise,Symbol(’x’, i), Symbol(’l’, j), K)
15 );
16 }
17
18 // Add an initial guess for the current pose
19 Values initialEstimate;
20 initialEstimate.insert(Symbol(’x’, i), initial_x[i]);
21
22 // Update iSAM with the new factors
23 isam.update(graph, initialEstimate);
24 }