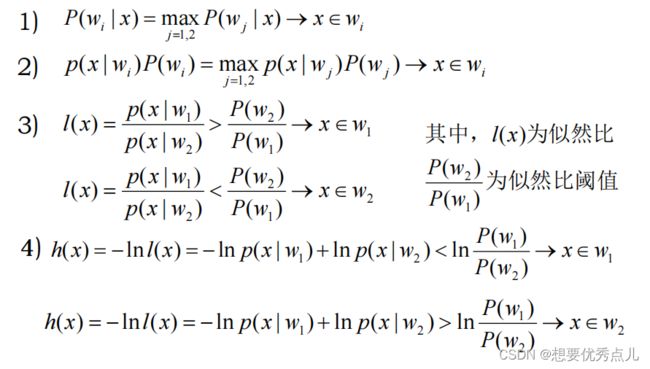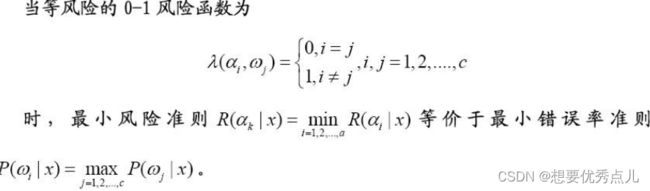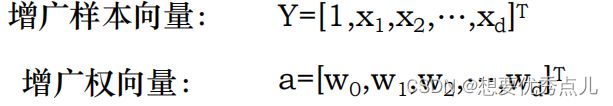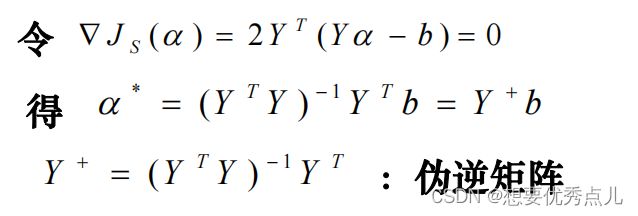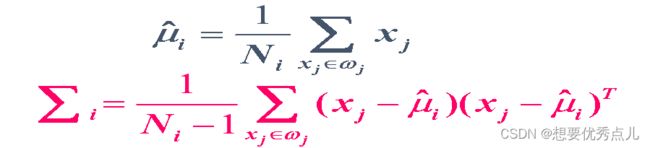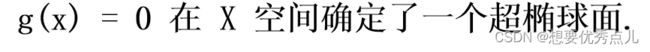模式识别期末复习问题合集
1.什么是模式?监督模式识别和非监督模式识别的典型过程分别是什么?
模式:指需要识别且可测量的对象的描述
2.基本的基于最小错误率的贝叶斯决策规则是什么?
4.多类问题中基于最小错误率的贝叶斯决策规则是什么?
例题:
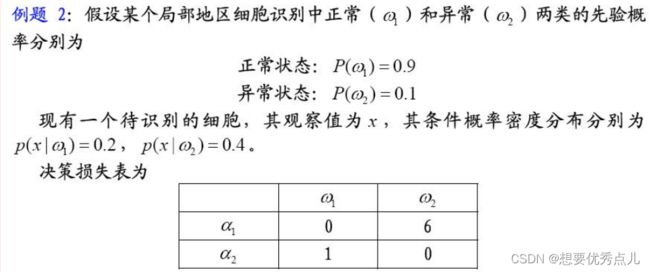
5.基于最小风险的贝叶斯决策规则是什么?
例题:
6. 基于最小错误率的贝叶斯决策与最小风险的贝叶斯决策是什么关系?
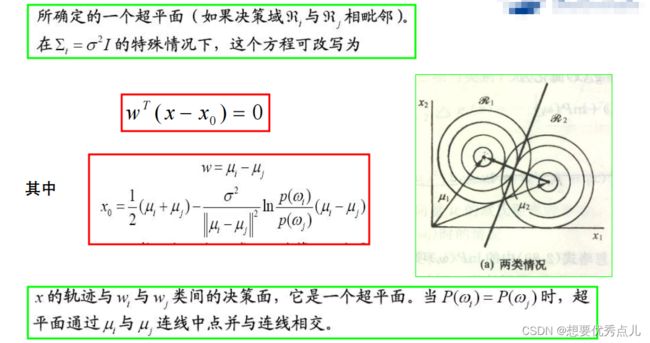
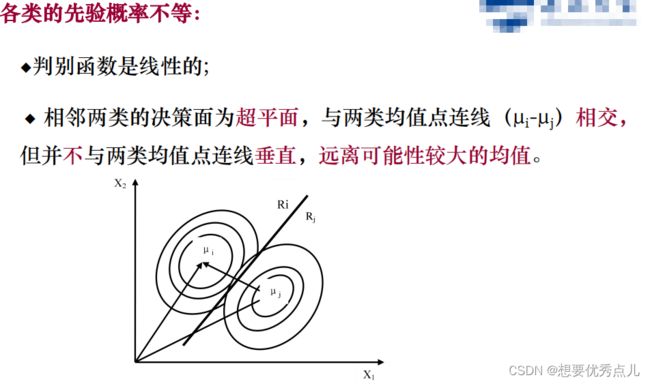
7.在正态分布概率模型下,当各类的协方差矩阵相等,并且都是对角阵时,各类的判别函数形式是什么?其分类面有什么特点?各类别的先验概率是否相等对分类面有什么影响?
(1)判别函数
(2)分类面
8.在正态分布概率模型下,当各类的协方差矩阵相等,均值任意,各类的判别函数形式是什么?其分类面有什么特点?各类别的先验概率是否相等对分类面有什么影响?
(1)判别函数
(2)分类面、先验概率
10.参数估计的主要工作是什么?
参数估计中,已知概率密度函数的形式,但其中部分或者全部参数未知,概率密度函数的估计问题就是用样本估计这些参数。
监督参数估计――样本所属类别(标签)已知,样本的类条件概率密度函数的形式已知,但参数未知(例如,已知高斯分布,但参数或未知),即已知规律但未知参数。
非监督参数估计――已知总体概率密度函数的形式,但样本所属类别未知,要求推断出概率密度函数的某些参数,称为非监督参数估计。
11.最大似然估计的基本思想是什么?
从样本中随机抽取n个样本,而模型的参数估计量使得抽取的这n个样本的观测值的概率最大。最大似然估计是一个统计方法,它用来求一个样本集的概率密度函数的参数。
12.什么是似然函数?对数似然函数的形式是什么?
![]()
13.贝叶斯估计的基本思想是什么?
是把待估计的参数本身也看作随机变量,然后根据观测数据对参数的分布进行估计。
14.非参数概率密度估计的原理是什么?
15.最大似然估计和贝叶斯估计的区别是什么?
最大似然估计是把待估计的参数当作未知但固定的参数,要做的是根据观测数据估计这个参数的取值;
贝叶斯估计则是把待估计的参数本身也看作随机变量,要做的是根据观测数据对参数的分布进行估计。
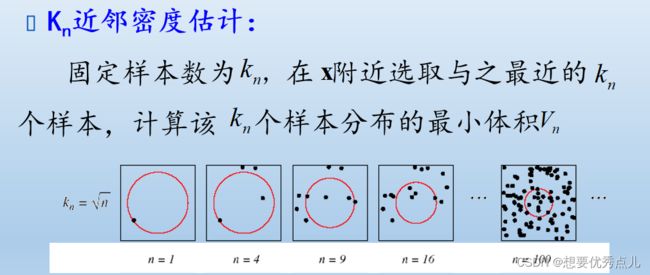
16.非参数的概率密度估计的方法有哪些?如何实现?
(1)Parzen窗估计
(2)kN近邻估计
17.如何根据训练样本直接设计分类器?思想是什么?
18. 线性判别函数的一般表达式是什么?各个参数有什么含义?
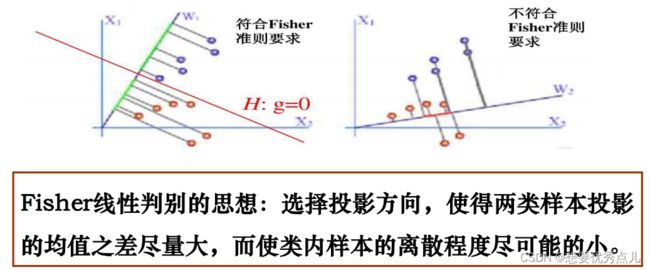
19.Fisher线性判别的基本思想是什么?
20. D维的样本经过投影后得到的是一个什么矢量还是一个标量?为什么?
矢量????
21.Fisher线性判别准则里的两个重要参数是什么?
最佳投影方向W*
22.按照Fisher线性判别准则得到的投影方向和决策面是什么关系?
Fisher判别函数最优的解本身只是给出了一个投影方向,并没有给出我们所关心的分类面,要得到分类面,需要在投影后的方向(一维空间)上确定一个分类阈值w0,过分类阈值并与投影方向垂直的超平面就是决策面。
23.决策面的位置由什么决定?
投影方向W*和分类阈值W0
24.什么是样本的增广化和规范化?
增广化:增加一维
规范化:
25. 在解空间中的解向量应该满足什么条件?
26.感知器准则函数的形式是什么?有什么含义?
27. 梯度下降法求解感知器准则函数的原理是什么?
28.批处理的感知器算法是怎么实现的?
29.单样本修正中的固定增量法和变增量法指的是什么?用变增量法有什么好处?
用变增量发可以根据错分样本改变步长,可以减少迭代次数
在感知器准则中, 要求全部样本是线性可分的 。此时,经 过有限步的迭代梯度下降法就可以收敛到一个解向量a* 。 当样本不是线性可分时,如果仍然使用感知器算法,则算 法不会收敛。
30.最小平方误差判别的准则函数是什么?
这个函数的最小化主要有两类方法:伪逆法求解和梯度下降法求解
①伪逆法求解:Js(a)在机制处对a的梯度应该为0,依次可以得到:
②梯度下降法:
31.widrow-hoff算法的思想是什么?
同样也是梯度下降算法:
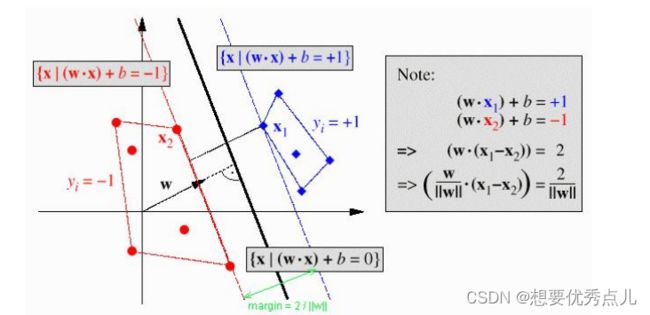
32.什么是最优分类超平面?
34.支持向量机的工作原理?
支持向量机的主要思想是:建立一个最优决策超平面,使得该平面两侧距离该平面最近的两类样本之间的距离最大化,从而对分类问题提供良好的泛化能力。
对于一个多维的样本集,系统随机产生一个超平面并不断移动,对样本进行分类,直到训练样本中属于不同类别的样本点正好位于该超平面的两侧,满足该条件的超平面可能有很多个,SVM正式在保证分类精度的同时,寻找到这样一个超平面,使得超平面两侧的空白区域最大化。
支持向量机中的支持向量是指训练样本集中的某些训练点,这些点最靠近分类决策面,是最难分类的数据点。SVM中最优分类标准就是这些点距离分类超平面的距离达到最大值;“机”是机器学习领域对一些算法的统称,常把算法看做一个机器,或者学习函数。
SVM是一种有监督的学习方法,主要针对小样本数据进行学习、分类和预测,类似的根据样本进行学习的方法还有决策树归纳算法等。
35.分段线性判别函数的基本思想是什么?
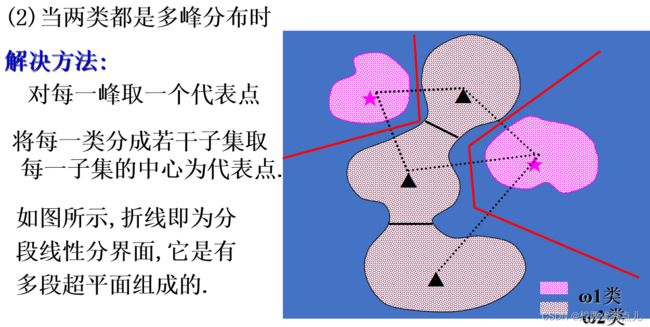
36. 当各类数据是多峰分布时,如何用基于最小距离的分类方法进行分类?
37.在样本每一类的子类数目已知,但是子类具体的划分情况未知的情况下,如何设计分段线性分类器?
38.当样本每一类的子类数量也无法确定时,如何设计分段线性分类器?
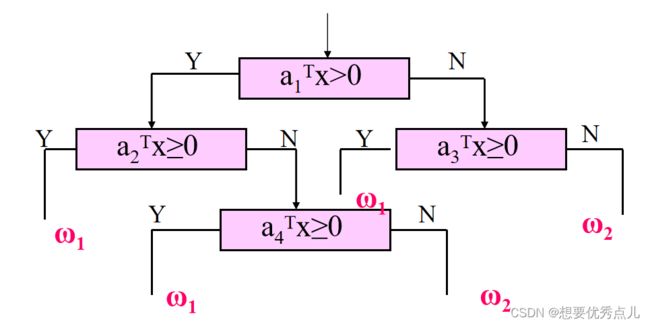
39.在设计二分树线性分类器时,初始权值对结果是否有影响?一般如何确定初始权值?
这种方法对初始权向量的选择很敏感,其结果随初始权向量的不同而大不相同。此外,在每个节点上所用的寻找权向量ai的方法不同,结果也将各异。通常可以选择分属两类的欧氏距离最小的一堆样本,取其垂直平分面的法向量作为a1的初始值,然后求得局部最优就a1*作为第一段超平面的法向量。对包含两类样本的各自类的划分也可以采用同样的方法。
40.二次判别函数确定的决策面是什么曲面?
它确定的决策面是一个超二次曲面,包括超球面、超椭球面、超双曲面等。
41.当两类样本符合正态分布时,
1)如何定义每一类的判别函数?
2)如何确定判别函数中的相关参数?
3)如果是两类问题,其决策面是什么?
4)如果出现错误时,可以采用什么调节方法来减少错误率?
2)确定判别函数中的相关参数
3)如果是两类问题,其决策面是什么?
直线,超平面,双曲线等等二次曲面
4)如果出现错误时,可以采用什么调节方法来减少错误率?
通过选择合适的Ki来减少错误率
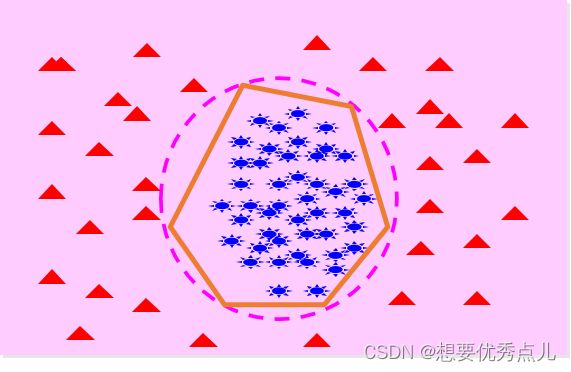
42.如果一类样本呈现团状分布,另外一类样本均匀分布在其周围时,如何进行决策?决策面是什么形状?
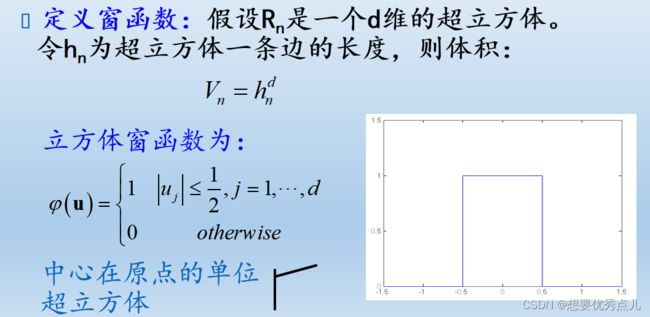
43.使用Parzen窗法进行概率密度函数估计时的方法是什么?(第三章)
计算样本xi是否落到小窗中,定义窗函数,反映了一个观测样本xi对在x处的概率密度估计的贡献,与样本xi与x的距离有关。
44. 非监督模式识别与监督模式识别的区别是什么?
45.非监督模式识别的基本思想是什么?非监督模式识别的方法分为哪两类?
46.聚类的基本思想是什么?
我们认为,所研究的样品或指标(变量)之间存在程度不同的相似性(亲疏关系)。于是根据一批样品的多个观测指标,具体找出一些能够度量样品或指标之间相似程度的统计量,以这些统计量作为划分类型的依据,把一些相似程度较大的样品(或指标)聚合为一类,把另外一些彼此之间相似程度较大的样品(或指标)聚合为另一类......关系密切的聚合到一个小的分类单位,关系疏远的聚合到一个大的分类单位,直到把所有的样品(或指标)都聚合完毕,把不同的类型一一划分出来,形成一个由小到大的分类系统。最后再把整个分类系统画成一张分群图(又称谱系图),用它把所有的样品(或指标)间的亲疏关系表示出来。
47 .动态聚类方法的三个要点是什么?
48.C均值算法的准则函数是什么?
49.C均值算法中确定初始代表点的方法有哪些?
50.C均值算法中如何对样本进行初始分类?
51. C均值算法有什么缺点?
52.K-L变换是如何应用于人脸识别的?