卷积神经网络以及经典网络模型的浅谈
“ML炼丹路上的小学徒”,记录学习过程中的所见所闻,CSDN上佛系更新,要是觉得不错,可以来访我的博客:fangkaipeng.com,第一时间在个人网站上更新,无广告无利益,有更好的阅读和互动体验。
1. 背景知识
1.1 痛点与解决
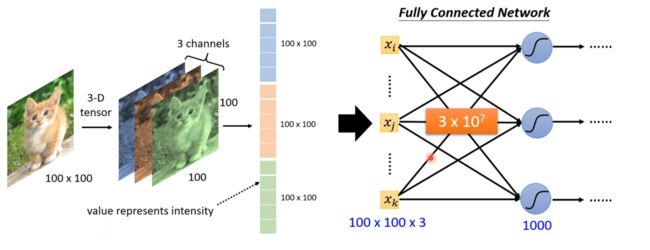
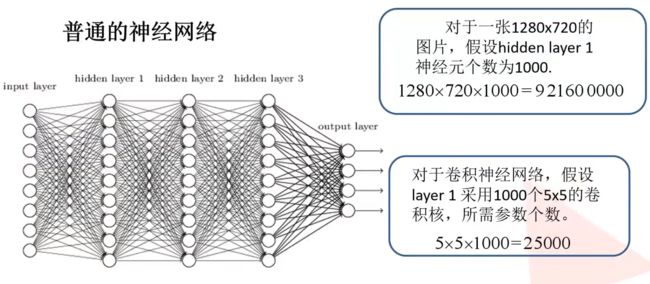
全连接的神经网络已经可以有很好的表现了,那么为什么还需要卷积神经网络呢?卷积神经网络实际就是在进行全连接层之前加入了一些卷积层和池化层,其目的在于特征提起。在图片识别领域,我们知道对于一张100 * 100 的RGB图像,有3个通道,可以表示成一个三维的tensor(可以理解成一个维度分别为长、宽、通道的矩阵),一共有30000个像素,而全连接层能接受的输入是一个一维向量,一种最直观的办法就行将整个tensor拉直,变成一条向量,一共有30000个元素,那么假设隐藏层有1000个神经元,那么单单一层网络就会有 3 e 7 3e^7 3e7 个权重,何况这只是对于一张图片的一层网络。实际运用中,数据集可能有上万张图片,神经网络也可能有好几个隐藏层,如果都是单纯地将矩阵拉成一个向量,那么计算量是无法想象的。并且参数越多,模型也越容易出现过拟合的问题,这也是我们不想看到的。
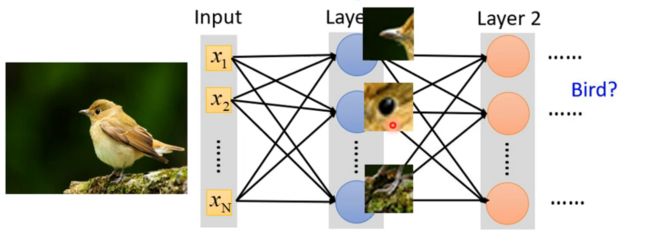
类似于人眼分类物体,我们其实不需要识别整张图片是什么,而是去识别图片中的特征,然后通过多个特征综合判断这是什么物体。比如如果识别下面这只鸟,可以先识别出鸟嘴、鸟眼睛、鸟爪,然后对这些特征进行全连接判读是否是鸟,相比全连接所有像素,全连接特征是一个很好的办法,这也是CNN卷积层所做的事。
举例来说,我们可以每次取图像的一小块区域进行特征识别后,将其作为输入传给全连接层进行训练,在CNN的卷积层中,这样的一小块区域又叫做卷积核,卷积核会在图像上不断移动,然后将其所覆盖的区域进行特征识别然后作为输入传递给下一层。卷积核的大小没有限制,也可以识别不同的通道,并且覆盖的区域可以重叠,这些都是一种超参数,由人为设定。

1.2 发展历史
1986年 Rumelhart和Hinton等人提出反向传播(BP)算法
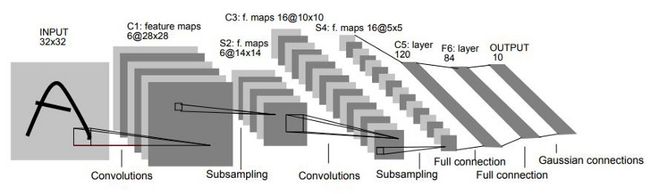
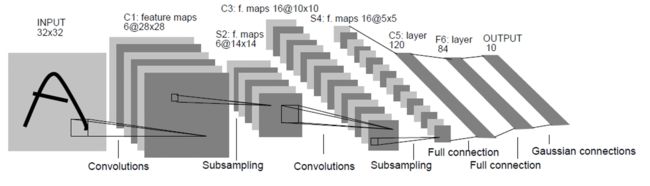
【论文连接】**LeNet:**1998年 LeCun利用BP算法训练LeNet5网络,包括卷积层、pooling层、全连接层,标志CNN真正面世,结构如下:
2006年 Hinton在Science Paper 首次提出Deep Learning的概念
【论文连接】**AlexNet:**2012年 Hinton的学生Alex Krizhevsky 在ImageNet的竞赛中使用AlexNet,刷新了image classification的记录
【论文连接】VGG: 来自 Andrew Zisserman 教授的组 (Oxford),在2014年的 ILSVRC localization and classification 两个问题上分别取得了第一名和第二名。
【论文连接】**GoogLeNet:**提出Inception结构是主要的创新点,其使用使得之后整个网络结构的宽度和深度都可扩大,能够带来2-3倍的性能提升。
【论文连接】**ResNet:**深度残差网络,是由中国广东的何凯明大神在2015年CVPR上提出来的,就在ImageNet中斩获图像分类、检测、定位三项冠军,解决了CNN网络深度的重大问题。
下图展示了一些经典模型的准确率和参数数量。
2. CNN的结构
2.1 全连接层
卷积层其实就是ANN(人工神经网络)的基础上加入了卷积层和池化层,使用先来介绍一下ANN中最核心的部分,全连接层。
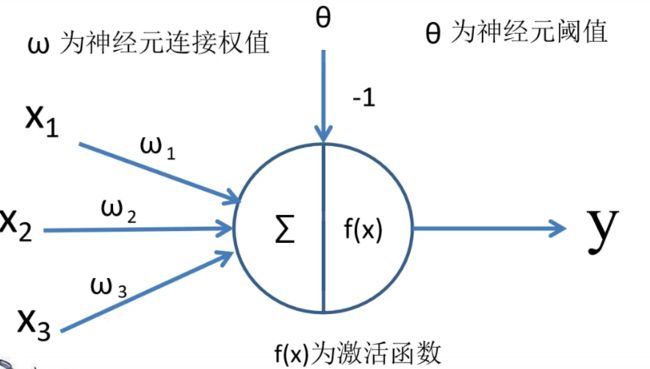
单个神经元结构如下图所示,这也是一个基本的感知机模型,输入的 x i x_i xi 乘上权重后相加再经过一个激活函数就是这个神经元的输出,即 y = f ( x 1 ⋅ ω 1 + x 2 ⋅ ω 2 + x 3 ⋅ ω 3 − 1 ) y=f\left(x_{1} \cdot \omega_{1}+x_{2} \cdot \omega_{2}+x_{3} \cdot \omega_{3}-1\right) y=f(x1⋅ω1+x2⋅ω2+x3⋅ω3−1)。
全连接层,是每一个神经元都与上一层的所有结点相连,用来把前边提取到的特征综合起来。由于其全相连的特性,一般全连接层的参数也是最多的。如下图的神经网络就是由若干个全连接层组成,其中在ANN中Layer0又称为输入串,Later3又称为输出层,中间的都成为隐藏层。
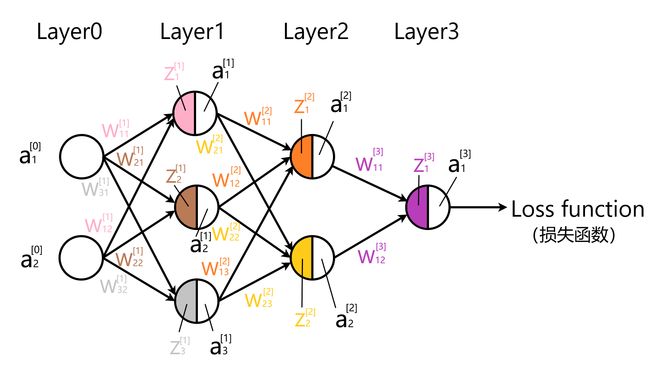
关于前向传播、反向传播以及神经网络可以看:机器学习:神经网络(一) 机器学习:神经网络(二)
2.2 卷积层
卷积操作
前面已经介绍过了,传统的ANN无法处理图像识别问题(数据量过大),于是在使用全连接层之前加入卷积层来提取特征,使得在不影响数据效果的前提下对数据实现降维,这一操作通过卷积核进行卷积实现的。单次卷积操作如下图所示,就是将卷积核与其覆盖的位置对应相乘然后将结果相加,放到输出的对应位置上,其中卷积核中的值是通过反向传播训练学习得到的,无需人为设置。

卷积的参数有:
- 卷积核大小(kernel size)表示每次选取识别特征的区域(一般为正方形)
- 步长(stride)表示卷积核每次移动的距离
- 填充(padding)表示是否在像素矩阵外填充0,这可以影响卷积层输出的矩阵大小

同卷积运行步骤如下图所示,每一步的操作就是上图所示的区域相乘再相加的过程:
| No padding, no strides | Arbitrary padding, no strides | Half padding, no strides | Full padding, no strides |
| No padding, strides | Padding, strides | Padding, strides (odd) |
图片出处:Convolution arithmetic
自定义可视化操作:Convolution Visualizer
卷积的特性
如下图,左边是全连接,右边是局部连接。对于一个1000 × 1000的输入图像而言,如果下一个隐藏层的神经元数目为10^6个,采用全连接则有1000 × 1000 × 10^6 = 10^12个权值参数,如此数目巨大的参数几乎难以训练;而采用局部连接,隐藏层的每个神经元仅与图像中10 × 10的局部图像相连接,那么此时的权值参数数量为10 × 10 × 10^6 = 10^8,将直接减少4个数量级。
图片有一个特性:图片的底层特征是与特征在图片中的位置无关的,比如说下图的两只鸟,一只的嘴在图片上方,一只在中间,无论在哪,它们都可以用一个提取鸟嘴特征的卷积核提取出来。由于卷积核的参数也是通过学习而来的,假设有一个卷积核学习得到的参数就是用来识别鸟嘴这一个特征的,那么我们就可以用这一个卷积核来逐一处理图片中的每个小区域来提取区域中是否存在鸟嘴。

在局部连接改进的基础上,我们可以通过权值共享,使得需要训练的参数进一步减少。在局部连接中,图片的一个子区域作为一个神经元的输入,但是每个神经元的参数是独立的需要分别进行训练。但是我们发现,对于提取同一个特征的卷积核,我们训练出来的权值是可以共享的,即这些神经元上的参数可以是一样的。注意这里是只提取某个特定的特征(如眼睛、鼻子等),而如果需要更多的特征,可以通过增加卷积核来增加通道实现。
综上,我们可以知道卷积最重要的两大特性:
- 拥有局部感知机制
- 权值共享,这也使得运算的规模大幅下降
相关参数的计算
-
卷积核的channel和输入特征层的channel相同(注:channel表示色彩通道数,RGB为3通道)
-
输出的特征矩阵channle与卷积核个数相同。
-
卷积操作后,输出矩阵的尺寸大小只与输入图片大小 W * W,卷积核大小 F * F ,步长S,padding的像素数P决定,计算公式为: N = ( W − F + 2 P ) / S + 1 N = (W-F+2P)/S+1 N=(W−F+2P)/S+1
2.3 池化层
池化层也类似于卷积层,也是有一个核在矩阵中移动,其目的是对特征图进行稀疏处理,减少数据运算量,池化层有很多类,主要是计算方式不同,下面以MaxPooling最大下采样为例:

3. 误差和优化器
3.1 SoftMax函数

计算误差之前需要先进行前向传播得到输出,如上图所示的一个神经网络,和普通神经网络不同的是,输出使用了Softmax函数作为激活函数,其好处是经过Softmax函数处理后的输出节点概率和为1,计算方法为: O i = e y i ∑ j e y j O_{i}=\frac{e^{y_{i}}}{\sum_{j} e^{y_{j}}} Oi=∑jeyjeyi,对于上面的网络,计算公式为:
O 1 = e y 1 e y 1 + e y 2 O 2 = e y 2 e y 1 + e y 2 O_{1}=\frac{e^{y_{1}}}{e^{y_{1}}+e^{y_{2}}} \quad O_{2}=\frac{e^{y_{2}}}{e^{y_{1}}+e^{y_{2}}} O1=ey1+ey2ey1O2=ey1+ey2ey2
3.2 误差的计算

损失函数|交叉熵损失函数
3.3 权重的更新
计算得到误差后,求偏导得到梯度即可进行反向传播,更新权重。但是这有一个问题,若使用整个样本集进行求解则损失梯度指向全局最优方向(如下图左),这是没问题的。但是在实际应用中往往不可能一次性将所有数据载入,内存(算力也不够),比如lmageNet项目的数据库中有超过1400万的图像数据,所以只能分批次(batch)训练。若使用分批次样本进行求解,损失梯度指向当前批次最优方向(如下图右),这就有可能导致进入局部最优解。

所以这里就需要使用一些优化器进行权重的更新,而不是简单地使用梯度乘以学习率来更新权重。
SGD优化器
计算公式为: w t + 1 = w t − α ⋅ g ( w t ) w_{t+1}=w_{t}-\alpha \cdot g\left(w_{t}\right) wt+1=wt−α⋅g(wt),其中$ \alpha$ 为学习率, g ( w t ) g\left(w_{t}\right) g(wt) 为 t t t 时刻对参数 w t w_{t} wt 的损失梯度,这就是最基础的优化器,其缺点在于易收到样本干扰,容易陷入局部最优解。
SGD+Momentum优化器
计算公式:
v t = η ⋅ v t − 1 + α ⋅ g ( w t ) w t + 1 = w t − v t \begin{array}{l} v_{t}=\eta \cdot v_{t-1}+\alpha \cdot g\left(w_{t}\right) \\ w_{t+1}=w_{t}-v_{t} \end{array} vt=η⋅vt−1+α⋅g(wt)wt+1=wt−vt
$ \alpha$ 为学习率, $g\left(w_{t}\right) $为 $ t$ 时刻对参数 w t w_{t} wt 的损失梯度 $\eta(0.9) $ 为动量系数
Adagrad优化器(自适应学习率)
计算公式:
s t = s t − 1 + g ( w t ) ⋅ g ( w t ) w t + 1 = w t − α s t + ε ⋅ g ( w t ) \begin{array}{l} s_{t}=s_{t-1}+g\left(w_{t}\right) \cdot g\left(w_{t}\right) \\ w_{t+1}=w_{t}-\frac{\alpha}{\sqrt{s_{t}+\varepsilon}} \cdot g\left(w_{t}\right) \end{array} st=st−1+g(wt)⋅g(wt)wt+1=wt−st+εα⋅g(wt)
α \alpha α 为学习率, $g\left(w_{t}\right) $ 为 t t t 时刻对参数 $ w_{t}$ 的损失梯度 $\varepsilon\left(10^{-7}\right) $ 为防止分母为零的小数,其缺点在于学习率下载太快,可能没收敛就停止训练了。
RMSProp优化器(自适应学习率)
计算公式:
$ \begin{array}{l}
s_{t}=\eta \cdot s_{t-1}+\underline{(1-\eta)} \cdot g\left(w_{t}\right) \cdot g\left(w_{t}\right) \
w_{t+1}=w_{t}-\frac{\alpha}{\sqrt{s_{t}+\varepsilon}} \cdot g\left(w_{t}\right)
\end{array}$
α \alpha α 为学习率, g ( w t ) g\left(w_{t}\right) g(wt) 为 t t t 时刻对参数 $w_{t} $ 的损失梯度 η ( 0.9 ) \eta(0.9) η(0.9) 控制衰减速度, $\varepsilon\left(10^{-7}\right) $ 为防止分母为零的小数。
Adam优化器(自适应学习率)
m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g ( w t ) v t = β 2 ⋅ v t − 1 + ( 1 − β 2 ) ⋅ g ( w t ) ⋅ g ( w t ) m ^ t = m t 1 − β 1 t v ^ t = v t 1 − β 2 t w t + 1 = w t − α v ^ t + ε m ^ t \begin{array}{l} m_{t}=\beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g\left(w_{t}\right) \\ v_{t}=\beta_{2} \cdot v_{t-1}+\left(1-\beta_{2}\right) \cdot g\left(w_{t}\right) \cdot g\left(w_{t}\right) \\ \hat{m}_{t}=\frac{m_{t}}{1-\beta_{1}^{t}} \ \ \ \ \ \hat{v}_{t}=\frac{v_{t}}{1-\beta_{2}^{t}} \\ w_{t+1}=w_{t}-\frac{\alpha}{\sqrt{\hat{v}_{t}+\varepsilon}} \hat{m}_{t} \end{array} mt=β1⋅mt−1+(1−β1)⋅g(wt)vt=β2⋅vt−1+(1−β2)⋅g(wt)⋅g(wt)m^t=1−β1tmt v^t=1−β2tvtwt+1=wt−v^t+εαm^t
$ \alpha $ 为学习率, $ g\left(w_{l}\right) $ 为 $t $ 时刻对参数 $w_{t} $ 的损大梯度 $\beta_{1}(0.9) $、 $\beta_{2}(0.999) $ 控制衰减速度, ε ( 1 0 − 7 ) \varepsilon\left(10^{-7}\right) ε(10−7) 为防止分母为零的小数。
下图是不同优化器寻找最优解的动画。
4. LeNet网络
4.1 结构分析
LeNet网络论文: Gradient-Based Learning Applied to Document Recognition
下面用PyTorch搭建一下LeNet网络(如下图),可以看见LeNet包含一个卷积层、一个池化下采样层、一个卷积层、一个池化下采样层、3个全连接层。
注: 由于上图结构输入的图像是灰度图像,通道只有1,而本次我们使用的数据集为RGB图像,通道为3,所以每层的卷积核个数不与图中一一对应,只保持结构大致相同。
卷积层conv1: Kernel: 16 kernel_size: 5 padding: 0 stride: 1 input_size:[3,32,32] out_size: [16,28,28]
池化层pool1: kernel_size: 2 padding: 0 stride: 2 input_size: [16,28,28] out_size: [16,14,14]
卷积层conv2: Kernel: 32 kernel_size: 5 padding: 0 stride: 1 input_size: [16,14,14] out_size: [32,10,10]
池化层pool2: kernel_size: 2 padding: 0 stride: 2 input_size: [32,10,10] out_size: [32,5,5]
全连接层FC1: 3255 输出结点数:120
全连接层FC2: 输入结点数:120 输出结点数:84
全连接层FC3:输入结点数:84 输出节点数(分类数目):10
4.2 数据处理
关于PyTorch的操作可以看我的博客: https://fangkaipeng.com/?cat=88
本次训练数据集来自CIFAR10,训练集有50000张图片,测试集10000张图片,有10个类别,是一个RGB的图像数据集,在PyTorch Tensor中,维度的排列顺序为 [bath, channel, height, width],其中bath表示一次处理图片的数量(由于图片过多,内存放不下,所以一般分批次使用训练集)。
本次数据处理比较简单主要步骤:
- 定义两个转换函数,一个用于将图片转换成tensor,另外一个将tensor进行标准化
- 载入测试数据和训练数据
- 将测试数据和训练数据打包,设置一个batch包含图片的数量,训练集将打乱顺序,而测试集按顺序打包。
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
transform = transforms.Compose(
[
transforms.ToTensor(), # 图片转tensor
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)) # 输入数据标准化
]
)
# 函数参数依次为:数据路径,是否为训练集,转换函数,是否下载
train_data = datasets.CIFAR10(root="../Dataset/CIFAR10", train=True, transform=transform, download=False) # 训练50000张
test_data = datasets.CIFAR10(root="../Dataset/CIFAR10", train=False, transform=transform, download=False) # 测试10000张
train_loader = DataLoader(train_data, batch_size=32, shuffle=True, num_workers= 0) # 将数据封装成一个个batch
test_loader = DataLoader(test_data, batch_size=10000, shuffle=False, num_workers=0)
4.3 网络搭建
from torch import nn
import torch.nn.functional as F
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
self.model = nn.Sequential(
nn.Conv2d(3, 16, 5), # input_size:[3,32,32] out_size: [16,28,28]
nn.Sigmoid(),
nn.AvgPool2d(2), # input_size: [16,28,28] out_size: [16,14,14]
nn.Conv2d(16, 32, 5), # input_size: [16,14,14] out_size: [32,10,10]
nn.Sigmoid(),
nn.AvgPool2d(2), # input_size: [32,10,10] out_size: [32,5,5]
nn.Flatten(), # 矩阵展开
nn.Linear(32 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10)
)
def forward(self, x):
x = self.model(x)
return x
4.4 训练模型
一般流程如下:
-
先实例化一个网络模型的对象
-
定义损失函数
-
定义优化器
-
设置epoch,即训练轮数
-
开始训练,对于每一个epoch:
-
从DataLoader中获取每个batch的数据,这是一个可迭代的对象:
-
数据放入实例化的网络中进行前向传播得到输出
-
计算损失
-
计算梯度
-
使用优化器更新参数
-
-
处理完所有batch后(即整个训练集训练完一次后),使用测试集进行评估准确率
-
-
处理完所有的epoch,训练结束,保存模型参数
此外还需要注意的是,如果需要用GPU运行,则需要将一下数据都放入GPU的内存中(要是用GPU运算还需要CUDA环境的支持):
- 实例化的模型
- 训练数据和测试数据
- 损失函数
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # 判断本机可用设备,优先使用GPU
# Pytorch中默认使用CPU,可用使用.to()函数指定使用GPU运算
net = LeNet().to(device=device) # 实例化网络并将其放入CPU中
loss_fn = nn.CrossEntropyLoss() # 实例化损失函数,这里使用交叉熵损失函数
loss_fn.to(device) # 损失函数放入GPU
optimizer = optim.Adam(net.parameters(), lr=0.005) # 定义优化器,使用Adam优化器
test_iter = iter(test_loader) # DataLoader是可迭代对象,使用iter获得迭代器
# 由于之前定义测试集的batch_size 为10000,即只有一个batch为整个数据集,所以只要取一个next就能获得所有测试集数据
test_imgs, test_labels = test_iter.next()
test_imgs = test_imgs.to(device) # 测试集数据放入GPU
test_labels = test_labels.to(device)# 测试集数据放入GPU
epoch = 20 # 设置训练轮数
print(device) # 输出一下当前本机可用设备是GPU还是CPU
print("------训练开始-----")
for i in range(epoch):
tot_loss = 0.0 # 总损失值
for data in train_loader: # 遍历训练集的DataLoader
imgs, labels = data # 获得训练集一个batch的图片和标签
imgs = imgs.to(device) # 放入GPU
labels = labels.to(device) # 放入GPU
outputs = net(imgs) # 前向传播得到输出
loss = loss_fn(outputs, labels) # 使用损失函数计算输出结果和标签的误差
optimizer.zero_grad() # 反向传播之前需要先清空一下梯度,非常重要!!不然梯度会累加
loss.backward() # 反向传播
optimizer.step() # 优化器优化
tot_loss = tot_loss + loss.item() # 累加损失值
with torch.no_grad(): # 一个epoch结束后测试模型,取消梯度跟踪
outputs = net(test_imgs) # 前向传播
predict_y = torch.max(outputs, dim=1)[1] # 得到预测结果,由于输出的是每个标签的概率,所以取最大值
accurcy = (predict_y == test_labels).sum().item() / test_labels.size(0) # 计算准确率
print("epoch= %d, loss = %.3lf, accury= %.3lf" %(i+1, tot_loss, accurcy))
tot_loss = 0.0
print("-----训练结束-----")
torch.save(net.state_dict(), "./train_result/LeNet.pth") # 保存模型
4.5 预测数据
预测数据流程如下:
- 载入模型
- 载入待测试的图片,转换成tensor
- 前向传播得到每个类别的概率,取最大的输出
import torch
import torchvision.transforms as transforms
from PIL import Image
from model import LeNet
transform = transforms.Compose(
[
transforms.Resize((32, 32)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]
)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
net = LeNet().to(device=device)
net.load_state_dict(torch.load("./train_result/LeNet.pth"))
im = Image.open("./predict_img/cat2.jfif")
im = transform(im)
im = im.to(device)
im = torch.unsqueeze(im, dim=0)
with torch.no_grad():
outputs = net(im)
predict = torch.max(outputs, dim=1)[1]
print(classes[int(predict)])
5. AlexNet网络
5.1 结构和创新点
【论文连接】
创新点
AlexNet是Alex小哥在自己的电脑上用两块 GTX 580 3GB GPUs 显卡捣鼓出来的模型,当时刷新了image classification的记录(自己捣鼓的东西直接成为SOTA,不愧是大神啊),除了模型结构外,AlexNet的主要创新点在于:
- 采用了ReLU作为激活函数,解决了Sigmoid函数在网络较深时出现的梯度消失问题,并且使用ReLU的速度也更快。
- 采用多GPU的方式训练(这更偏向于工程上的改进,在科研领域影响不大)
- 训练时使用Dropout方法随机失活一些神经元,在AlexNet中,主要是在最后的全连接层使用了这项技术,因为最后的全连接层非常大(4096 * 4096),这就导致很容易发生过拟合问题,Dropout本质也是一种正则项,可以有效地抑制过拟合问题。
- 使用重叠的最大池化,此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小,这样池化层的输出之间会有重叠和覆盖,提升了特征的丰富性。
- 提出了LRN层(局部响应归一化),增强了模型的泛化能力,但在后来被证明这是无效的操作,被Batch Normalization替代。
- 采用原始的RGB图像进行训练,开启了端到端的训练方式(虽然但是Alex没有意识到这一工作的重大意义)
结构
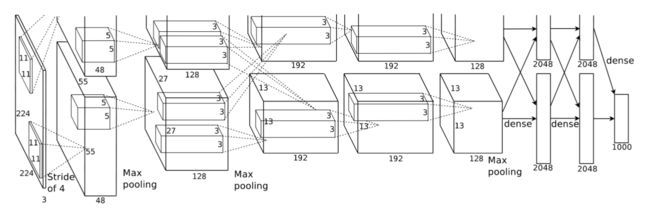
论文中给出模型的结构如下图所示,需要注意的是,Alex当时使用了两块GPU进行模型并行化,所以下图展示的是一个完整的模型(底部),以及半个模型(顶部),两个相同的模型分别在两个GPU中进行训练,并在第3个卷积层以及后面的全连接层中进行了数据交流。
由于Alex使用并行化实现,上下两个模型是一样的,我们将其合并起来也可能当做一个完整的AlexNet网络,它由5个卷积层和3个全连接层实现,具体参数如下:
- Input 层,输入为 3 * 224 * 224 的图片(分别对应通道–长–宽,下同)
- Conv1层,采用 96 个 3 * 11 * 11 的卷积核,步长为 4 ,padding为2 ,得到输出为 96 * 55 * 55 的特征矩阵(这里是96是因为把两个并行模型合并了)
- MaxPool1层,池化核为 3 * 3,步长为2, 得到特征矩阵为 96 * 27 * 27
- Conv2层,使用了 256 个 96 * 5 * 5 的卷积核,步长为1, padding为2,输出的特征矩阵为 256 * 27 * 27
- MaxPool2层,池化核为 3 * 3,步长为2, 得到特征矩阵为 256 * 13 * 13
- Conv3层,使用 384 个 256 * 3 * 3 的卷积核,步长为1, padding为1,输出特征矩阵为 384 * 13 * 13
- Conv4层,使用 384 个 384 * 3 * 3 的卷积核,步长为1, padding为1,输出特征矩阵为 384 * 13 *13
- Conv5层, 使用 256个 384 * 3 * 3 的卷积核,步长为1,padding为1,输出特征矩阵为 256 * 13 * 13
- MaxPool3层,池化核为 3 * 3,步长为2, 得到特征矩阵为 256 * 6 * 6
- FC6层,全连接层,扁平化成 1 *9216的输入,输出为 1 *4096
- Dropout6层,以0.5的概率随机失活,输出维度不变
- FC7层,输出还是 1 * 4096
- Dropout7层,以0.5的概率随机失活,维度不变
- FC8层,输出维度为1 * 1000
5.2 代码实现
模型搭建
模型中主要包括网络结构的搭建和权值初始化,按照论文中的说法,对于所有层的输出都进行标准化,使得数据成高斯分布,方差为0.01,均值为0,对于第2、4、5个卷积层和所有的全连接层的偏置置为0。另外,在每两个全连接层之间加入一个概率为0.5的Dropout,一共有两个Dropout层。
import torch.nn as nn
from torchvision import datasets, transforms
import torch
class AlexNet(nn.Module):
def __init__(self, class_num=100, init_weights=False):
super(AlexNet, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 96, kernel_size=11, stride=4, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(96, 256, kernel_size=5, stride=1, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(256, 384, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 384, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384, 256, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(start_dim=1), # 按照第一维度展开,因为tensor进来的第0维为batch
nn.Linear(256 * 6 * 6, 4096),
nn.ReLU(inplace=True),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096),
nn.ReLU(inplace=True),
nn.Dropout(p=0.5),
nn.Linear(4096, class_num)
)
if init_weights:
self.initialize_wights()
def forward(self, x):
x = self.features(x)
return x
def initialize_wights(self):
idx = 0
for m in self.modules():
if isinstance(m, nn.Conv2d):
idx = idx + 1
nn.init.normal_(m.weight, 0, 0.01)
if m.bias is not None and (idx in [2, 4, 5]):
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
数据预处理
对于输入的数据,论文中的做法是将图片先按照短边将图片等比缩放到宽为256的图片,然后按照中心裁剪成256*256,接着再随机在256 * 256 的图片中提取出一个224 * 224的图片并随机进行翻转,这样做的好处是增加了随机性,减少过拟合的问题。这里为了方便,直接将图片随机裁剪成224 * 224,然后再随机翻转。论文中对训练集的一个batch大小设置为128,这里和论文中保持一致,但我采用的是CIFAR100数据集进行训练。
data_transform = {
"train": transforms.Compose([transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]),
"val": transforms.Compose([transforms.Resize((224, 224)), # cannot 224, must (224, 224)
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])}
train_data = datasets.CIFAR100(root='../Dataset/CIFAR100', train=True, transform=data_transform['train'],
download=True)
validate_data = datasets.CIFAR100(root='../Dataset/CIFAR100', train=False, transform=data_transform['val'],
download=True)
batch_size = 128
nw = min([os.cpu_count(), batch_size if batch_size > 1 else 0, 8]) # number of workers
print('Using {} dataloader workers every process'.format(nw))
train_loader = torch.utils.data.DataLoader(train_data,
batch_size=batch_size, shuffle=True,
num_workers=nw)
validate_loader = torch.utils.data.DataLoader(validate_data,
batch_size=4, shuffle=False,
num_workers=nw)
训练模型
在论文中,主要有以下几个细节需要注意:
- 采用SGD优化器,momentum=0.9,weight_decay =0.0005
- 学习率设置为0.01,当损失值不变化时,将学习率缩小10倍
net = AlexNet(class_num=100, init_weights=True)
net.to(device)
loss_function = nn.CrossEntropyLoss()
# pata = list(net.parameters())
optimizer = optim.Adam(net.parameters(), lr=0.0002)
epochs = 10
save_path = './AlexNet.pth'
best_acc = 0.0
train_steps = len(train_loader)
for epoch in range(epochs):
# train
net.train()
running_loss = 0.0
train_bar = tqdm(train_loader, file=sys.stdout)
for step, data in enumerate(train_bar):
images, labels = data
optimizer.zero_grad()
outputs = net(images.to(device))
loss = loss_function(outputs, labels.to(device))
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
train_bar.desc = "train epoch[{}/{}] loss:{:.3f}".format(epoch + 1,
epochs,
loss)
# validate
net.eval() # 进入评估模式,取消dropout
acc = 0.0 # accumulate accurate number / epoch
with torch.no_grad():
val_bar = tqdm(validate_loader, file=sys.stdout)
for val_data in val_bar:
val_images, val_labels = val_data
outputs = net(val_images.to(device))
predict_y = torch.max(outputs, dim=1)[1]
acc += torch.eq(predict_y, val_labels.to(device)).sum().item()
val_accurate = acc / len(validate_data)
print('[epoch %d] train_loss: %.3f val_accuracy: %.3f' %
(epoch + 1, running_loss / train_steps, val_accurate))
if val_accurate > best_acc:
best_acc = val_accurate
torch.save(net.state_dict(), save_path)
print('Finished Training')
6. VGG网络
6.1 VGG网络介绍
VGG网络是在论文 VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION 中被提出来的,作者来自牛津大学 Visual Geometry Group 组,VGG也取自该组的单词首字母。VGG网络的这篇文章是面向ImageNet竞赛产生的,主要是为了解决ImageNet中的1000类图像分类和 localization问题。VGG网络在当时获得了分类第二,localization第一的成绩(分类第一是当年的GoogLeNet)。在论文中,作者主要探究了卷积神经网络的深度和其性能之间的关系,介绍了一些模型训练时数据处理的技巧。
VGG网络以及这篇文章的主要贡献有:
- 通过采用 3 * 3的小卷积核取代大卷积核,作者发现,两个3 * 3卷积核的堆叠相对于5 * 5卷积核的感受野(receptive field),三个3 * 3卷积核的堆叠相当于7 * 7卷积核的感受野,使用更小的卷积核尺寸和stride使得参数减少,过拟合的问题也得到缓解,性能得到提高。
- 发现深度可以提升性能,于是VGG通过堆叠 3 * 3 的小卷积核成功搭建了16-19层的CNN。VGG网络将经典的CNN结构开发到了极致,并达到了深度的极致。在VGG之后出现的各种网络都是在模型结构上进行了改变(如GoogLeNet的inception结构和ResNet的残差结构)。
- 得益于网络深度和大量的小卷积核,使得VGG的泛化能力非常好,可以很好地迁移到其他数据集上。具体来说就是用VGG提取数据的特征,然后在最后加入一个简单的分类器就行(如SVM)。
- 训练时,先训练级别简单(层数较浅)的VGGNet的A级网络,然后使用A网络的权重来初始化后面的复杂模型,加快训练的收敛速度。
- 采用了Multi-Scale的方法来训练和预测。可以增加训练的数据量,防止模型过拟合,提升预测准确率。
- 网络测试阶段将训练阶段的三个全连接替换为三个卷积(第一个全连接层用 7 * 7的卷积层替换,后两个用 1 * 1 的卷积层替换)。对于训练和测试一样的输入维度下,网络参数量没有变化,计算量也没有变化,思想来自 Sermanet 的 OverFeat,1×1 的卷积思想则来自NIN。虽然没改变计算量,但是其优点在于全卷积网络可以接收任意尺度的输入以及得到任意尺寸的输出,使得可以很好的适应不同的数据集,同时使用 1 * 1 的卷积层不容易破坏图像的空间结构(全连接层的坏处就在于其会破坏图像的空间结构)。
如下图表示的是各种网络每百万参数对准确率的贡献是多少,可以看到VGG每百万参数量对准确率的贡献是很低的,这也说明VGG网络对参数的利用效率不高。虽然VGG网络十分臃肿,但直到现在还在被使用,主要由于其泛化能力非常好,在不同的图片数据集上都有良好的表现,所以依然经常被用来提取特征图像。

6.2 3 * 3卷积核
在论文中,作者实验发现,采用3 * 3 的卷积核能达到最好的效果,并且发现两个3 * 3卷积核的堆叠相对于5 * 5卷积核的感受野(receptive field),三个3 * 3卷积核的堆叠相当于7 * 7卷积核的感受野,如下图所示,黄色表示的是感受野,可以发现,经过两个3 * 3 的卷积,卷积核可以感受到的范围和一个 5 * 5的相同。
在论文中,作者通过实验得出以下几个结论:
- 1 * 1的卷积核本质就是一个线性变换和一次非线性激活,可以用于数据的升维和降维。但是1 * 1的卷积核不如 3 * 3 的卷积核,说明感受野也是很重要的。
- 在相同感受野的情况下,深层的小卷积效果比浅层大卷积好。
- 在AlexNet中使用过的LRN正则方法没有意义。
之所以选用 3 * 3的卷积核而不是用更小或者更大的卷积核,其原因在于这是最 ”中庸“ 的一个选择,使用更大的卷积核会导致参数量更大(在相同感受野下),而使用更小的卷积核会导致感受野不够,无法提取足够的特征,而 3 * 3的卷积核刚好是可以在上下左右四个方向都有涉及的最小区块。
6.2 VGG模型结构
在论文中,作者一共构造了6种形态的模型,其中模型A和模型A-LRN的区别在于A-LRN中加入了一个LRN正则化,用于探究LRN的作用,实验后发现LRN是没有意义的。所以总的来说作者一共提出了5个深度不同或卷积核大小不同的模型。其中模型D和模型E分别就是著名的 VGG-16 和 VGG-19。分别训练每个模型,作者得出结论:
- 通过比较B和C发现,加入 1 * 1的卷积核可以为模型带来不错的表示能力(非线性表达)
- 比较C和D发现,感受野的重要性更大,3 * 3 的卷积核比 1 * 1 的好
- 横向比较这些网络,发现网络越深,效果越好
VGG-16的详细模型结构:VGG-16
6.3 代码实现
由于有5中不同的VGG结构,而它们之间又有相似性,所以可以用配置表的方式,构造网络
import torch
from torch import nn
class VGG(nn.Module):
def __init__(self, features, num_classes=1000, init_weights=False):
super(VGG, self).__init__()
self.features = features
self.classifier = nn.Sequential(
nn.Dropout(p=0.5),
nn.Linear(512 * 7 * 7, 2048),
nn.ReLU(True),
nn.Dropout(p=0.5),
nn.Linear(2048, 2048),
nn.ReLU(True),
nn.Linear(2048, num_classes)
)
if init_weights:
self._initialize_weights()
def forward(self, x):
# N * 3 * 224 * 224
x = self.features(x)
# N * 512 * 7 * 7
x = torch.flatten(x, start_dim=1)
# N * (512*7*7)
x = self.classifier(x)
return x
def _initialize_weights(self):
for m in self.modules(): # 遍历网络所有层
if isinstance(m, nn.Conv2d): # 判断m的类型是否为nn.Conv2d
# nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu') # 在ReLU网络中表现更好
nn.init.xavier_uniform_(m.weight) # 初始化参数服从正态分布
if m.bias is not None:
nn.init.constant_(m.bias, 0) # 初始化整个矩阵为常数0
elif isinstance(m, nn.Linear):
nn.init.xavier_uniform_(m.weight)
# nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0) # 初始化整个矩阵为常数0
# 根据配置信息构造网络
def make_features(cfg: list):
layers = []
in_channels = 3
for v in cfg:
if v == 'M':
layers += [nn.MaxPool2d(2, 2)]
else:
conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
layers += [conv2d, nn.ReLU(True)]
in_channels = v
return nn.Sequential(*layers)
# 各种网络的配置信息,M表示一个MaxPool层,在VGG中size=2*2,其余的数字都表示卷积核的输出channel,因为卷积核大小也都是3*3不用记录。
cfgs = {
'vgg11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'vgg13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'vgg16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'vgg19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
def vgg(model_name="vgg16", **kwargs):
try:
cfg = cfgs[model_name]
except:
print("输入的模型 {} 不存在配置cfgs中,请检查".format(model_name))
exit(-1)
model = VGG(make_features(cfg), **kwargs)
return model
7. GoogLeNet
7.1 网络介绍
GoogLeNet在2014由Google团队提出,获得ImageNet中Classification任务的第一名,它比AlexNet参数少12倍的同时但更准确,网络中主要有一下几个亮点:
- 引入Inception结构
- 使用 1*1 的卷积核进行降维和映射处理
- 添加两个辅助分类器帮助训练
- 丢弃全连接层,使用平均池化层,大大减少了模型参数,低内存高效率使得其可以在移动设备上使用。
7.2 Inception结构
![]()
上图展示的是论文中的原图,左边为最原始的Inception结构,右边为改进后的结构。从图片来看Inception模块就用不同尺寸的卷积核同时对输入进行卷积操作,外加一个池化操作,最后把各自的结果汇聚在一起作为总输出(按照channel堆叠,每层输出具有相同的长宽尺寸)。与传统 CNN 的串联结构不同,inception模块使用了并行结构并且引入了不同尺寸的卷积核。其好处在于:
- 在多个尺度上同时进行卷积,能提取到不同尺度的特征,最后拼接意味着不同尺度特征的融合。
- 实现将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能
这里需要一提的是,在算法和模型角度提升网络性能的方法有增加网络的深度和宽度,比如VGG就是通过大量使用 3 * 3卷积核来增加网络深度,但是一味地增加会导致需要学习的参数增加,这也会带来两个问题:
- 巨大的参数容易发生过拟合
- 计算量大大增加
解决上述问题的方法是引入稀疏特性和将全连接层转换成稀疏连接(理论研究论文),但是,计算机软硬件对非均匀稀疏数据的计算效率很差,大量的文献表明可以将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能,于是就有了初版的Inception结构。
但是在初版的Inception结构中使用5x5的卷积核仍然会带来巨大的计算量,作者借鉴NIN,采用1x1卷积核来进行降维,得到了优化后的Inception结构,改进后的Inception结构输出的维度不变,但是参数了减少了大约4倍。
7.2 网络结构
GoogLeNet其实就是多个Inception结构的堆叠,由于Inception结构参数减少,使得GoogLeNet达到了22层的深度,但其参数还比AlexNet少了12倍左右,GoogLeNet网络的结构特点如下:
- 采用了模块化的结构,可以方便地增删和修改Inception结构;
- 网络最后采用了average pooling来代替全连接层,想法来自NIN,事实证明可以将TOP1 accuracy提高0.6%。但是,实际在最后还是加了一个全连接层,主要是为了方便以后大家finetune;
- 虽然移除了全连接,但是网络中依然使用了Dropout ;
- 为了避免梯度消失,网络额外增加了2个辅助的softmax用于向前传导梯度(辅助分类器)。辅助分类器是将中间某一层的输出用作分类,并按一个较小的权重(0.3)加到最终分类结果中,这样相当于做了模型融合,同时给网络增加了反向传播的梯度信号,也提供了额外的正则化,对于整个网络的训练很有裨益。此外,实际测试的时候,这两个额外的softmax会被去掉。
GooLeNet的网络结构可以见:GoogLeNet网络结构
7.3 代码实现
import torch.nn as nn
import torch
import torch.nn.functional as F
class GoogLeNet(nn.Module):
def __init__(self, num_classes=1000, aux_logits=True, init_weights=False):
super(GoogLeNet, self).__init__()
self.aux_logits = aux_logits
self.conv1 = BasicConv2d(3, 64, kernel_size=7, stride=2, padding=3)
self.maxpool1 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.conv2 = BasicConv2d(64, 64, kernel_size=1)
self.conv3 = BasicConv2d(64, 192, kernel_size=3, padding=1)
self.maxpool2 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.inception3a = Inception(192, 64, 96, 128, 16, 32, 32)
self.inception3b = Inception(256, 128, 128, 192, 32, 96, 64)
self.maxpool3 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.inception4a = Inception(480, 192, 96, 208, 16, 48, 64)
self.inception4b = Inception(512, 160, 112, 224, 24, 64, 64)
self.inception4c = Inception(512, 128, 128, 256, 24, 64, 64)
self.inception4d = Inception(512, 112, 144, 288, 32, 64, 64)
self.inception4e = Inception(528, 256, 160, 320, 32, 128, 128)
self.maxpool4 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.inception5a = Inception(832, 256, 160, 320, 32, 128, 128)
self.inception5b = Inception(832, 384, 192, 384, 48, 128, 128)
if self.aux_logits:
self.aux1 = InceptionAux(512, num_classes)
self.aux2 = InceptionAux(528, num_classes)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.dropout = nn.Dropout(0.4)
self.fc = nn.Linear(1024, num_classes)
if init_weights:
self._initialize_weights()
def forward(self, x):
# N x 3 x 224 x 224
x = self.conv1(x)
# N x 64 x 112 x 112
x = self.maxpool1(x)
# N x 64 x 56 x 56
x = self.conv2(x)
# N x 64 x 56 x 56
x = self.conv3(x)
# N x 192 x 56 x 56
x = self.maxpool2(x)
# N x 192 x 28 x 28
x = self.inception3a(x)
# N x 256 x 28 x 28
x = self.inception3b(x)
# N x 480 x 28 x 28
x = self.maxpool3(x)
# N x 480 x 14 x 14
x = self.inception4a(x)
# N x 512 x 14 x 14
if self.training and self.aux_logits: # eval model lose this layer
aux1 = self.aux1(x)
x = self.inception4b(x)
# N x 512 x 14 x 14
x = self.inception4c(x)
# N x 512 x 14 x 14
x = self.inception4d(x)
# N x 528 x 14 x 14
if self.training and self.aux_logits: # eval model lose this layer
aux2 = self.aux2(x)
x = self.inception4e(x)
# N x 832 x 14 x 14
x = self.maxpool4(x)
# N x 832 x 7 x 7
x = self.inception5a(x)
# N x 832 x 7 x 7
x = self.inception5b(x)
# N x 1024 x 7 x 7
x = self.avgpool(x)
# N x 1024 x 1 x 1
x = torch.flatten(x, 1)
# N x 1024
x = self.dropout(x)
x = self.fc(x)
# N x 1000 (num_classes)
if self.training and self.aux_logits: # eval model lose this layer
return x, aux2, aux1
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
class Inception(nn.Module):
def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch5x5red, ch5x5, pool_proj):
super(Inception, self).__init__()
self.branch1 = BasicConv2d(in_channels, ch1x1, kernel_size=1)
self.branch2 = nn.Sequential(
BasicConv2d(in_channels, ch3x3red, kernel_size=1),
BasicConv2d(ch3x3red, ch3x3, kernel_size=3, padding=1) # 保证输出大小等于输入大小
)
self.branch3 = nn.Sequential(
BasicConv2d(in_channels, ch5x5red, kernel_size=1),
BasicConv2d(ch5x5red, ch5x5, kernel_size=5, padding=2) # 保证输出大小等于输入大小
)
self.branch4 = nn.Sequential(
nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
BasicConv2d(in_channels, pool_proj, kernel_size=1)
)
def forward(self, x):
branch1 = self.branch1(x)
branch2 = self.branch2(x)
branch3 = self.branch3(x)
branch4 = self.branch4(x)
outputs = [branch1, branch2, branch3, branch4]
return torch.cat(outputs, 1)
class InceptionAux(nn.Module):
def __init__(self, in_channels, num_classes):
super(InceptionAux, self).__init__()
self.averagePool = nn.AvgPool2d(kernel_size=5, stride=3)
self.conv = BasicConv2d(in_channels, 128, kernel_size=1) # output[batch, 128, 4, 4]
self.fc1 = nn.Linear(2048, 1024)
self.fc2 = nn.Linear(1024, num_classes)
def forward(self, x):
# aux1: N x 512 x 14 x 14, aux2: N x 528 x 14 x 14
x = self.averagePool(x)
# aux1: N x 512 x 4 x 4, aux2: N x 528 x 4 x 4
x = self.conv(x)
# N x 128 x 4 x 4
x = torch.flatten(x, 1)
x = F.dropout(x, 0.5, training=self.training)
# N x 2048
x = F.relu(self.fc1(x), inplace=True)
x = F.dropout(x, 0.5, training=self.training)
# N x 1024
x = self.fc2(x)
# N x num_classes
return x
class BasicConv2d(nn.Module):
def __init__(self, in_channels, out_channels, **kwargs):
super(BasicConv2d, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, **kwargs)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
x = self.conv(x)
x = self.relu(x)
return x
8. ResNet
8.1 ResNet网络介绍
我们知道要提升网络性能,除了更好的硬件和更大的数据集以外,最主要的办法就是增加网络的深度和宽度,而增加网络的深度和宽度带来最直接的问题就是网络参数剧增,使得模型容易过拟合以及难以训练。在VGG中,通过使用 3 * 3的卷积核替代大卷积核实现将深度提升到了19层;在GoogLeNet中,通过引入Inception结构,实现将深度提升到22层,在BN-Inception中达到30层,还有很多例子都表明,越深的网络性能越好。
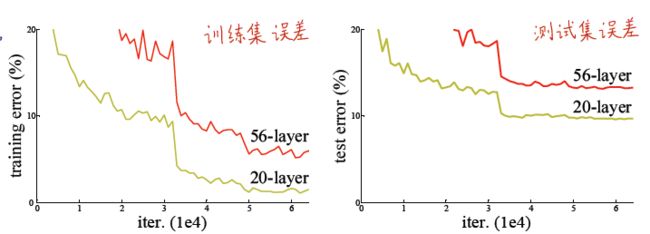
但是直接简单粗暴地堆叠深度,也导致了一个臭名昭著的问题:梯度爆炸/消失,使得网络无法收敛,不过通过适当的权值初始化和Batch Normalization 可以加快网络收敛。但是,当网络收敛后,又暴露出了一个问题,就是网络退化。当网络深度变深后,准确率开始达到饱和,然后迅速退化,并且这种现象不是由梯度消失和过拟合造成的。在论文中给出了如下的一张图,分别表示20层模型和56层模型在测试集和训练集的误差。从图中我们也可以看出,迭代到后面时,误差也是在波动的,说明梯度并没有消失,参数还在更新,并且无论在训练集测试集上,56层的错误率都远高于20层模型的,这也说明不是由过拟合导致的。(过拟合的现象是,在训练集上的误差小,但是在测试集上误差很大)
要解决网络退化问题,作者首先提出了一个解决办法,就是先构造一个浅模型,然后将得到浅模型的输出和原输入汇总(记为A)作为下一个浅模型的输入,下一个浅模型将输入A计算得到输出与输入A本身汇总成为下一个浅模型的输入,依次下去,如下图所示。这样做的好处是,将输入引入进来,可以使得模型训练后的效果至少不会比初始的输出差,最多也就是和输入相同,解决了网络退化的问题。进而作者提出了残差模型,具体关于残差 模块为什么可以解决网络退化问题,在下一节会进行介绍。

值得一提的是,ResNet来自的论文 Deep Residual Learning for Image Recognition 作者全部来自中国,其中第一作者何恺明是03年广东高考状元,单单这篇ResNet论文的Google引用达到了10万多,著名的参数初始化方法Kaiming初始化方法就是由他提出的,在PyTorch中也进行了实现(torch.nn.init.kaiming_uniform等),妥妥的超级大牛。
8.2 残差模块
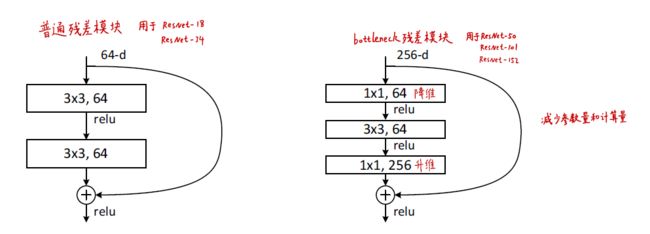
残差模块如下图所示,其中左边用于小型的ResNet网络,右边的用于大型的ResNet网络,之所以要增加1 * 1的卷积核,是为了通过升维和降维减少参数量和计算量。
残差模块解决网络退化的机理:
(恒等映射指的是输入和输出都一样的映射关系)
-
**深层梯度回传顺畅:**恒等映射这一路的梯度为1,把深层梯度注入底层,防止梯度消失。
-
传统线性结构网络难以拟合恒等映射: 什么都不做有时很重要,无论什么样的网络模型都很难做到输入和输出相同,而残差模块可以让模型自行选择是否要更新,同时弥补了高度非线性造成的不可逆的信息损失。
-
ResNet反向传播传回的梯度相关性好: 随着网络的加深,相邻像素反向传播来的梯度相关性就越来越低,最后基本无关,变成随机扰动。所谓的相关性,指的是,在图片中,一个像素周围的像素肯定是有一定联系的,比如耳朵上的像素周围也大概率是耳朵。残差模块的引入使得梯度相关性的衰减大幅减少,保持了梯度的相关性。
-
ResNet相当于几个浅层网络的集成: 如下图左所示,三个串联的残差模块可以看成多个浅层神经网络的组合,也就是说,对于 n 个残差模块,有 2 n 2^n 2n 个潜在的路径(这和Dropout的原理很像)。并且在测试阶段,去掉某几个残差块,几乎不影响性能,如下图右所示,去掉 f 2 f_2 f2 不会对模型造成很严重的影响,只是和 f 2 f_2 f2 相关的路无法通过了而已。
8.3 模型结构

图片来自论文,介绍了不同深度的ResNet结构。下图是34层的ResNet结构,对照表格分析可以得知,输入图片先经过一个 7 * 7的卷积层,然后是一个 3 * 3的最大池化层,接着在表格中分成了4个卷积结构,第一个卷积结构中是三个残差结构,该残差结构由两个 3 * 3 的卷积层组成;第二个卷积结构由 4 个残差结构组成,该残差结构由两个 3 * 3 的卷积核组成,依次类推,最后经过一个平均池化层,一个全连接层,一个softmax层输出结果。
8.4 代码实现
论文中一共介绍了两种残差模块,区别如下所示,一种是基础残差模块,用 BasicBlock 类实现,另外一个是Bottleneck模块,用 Bottleneck 类实现,在表格中我们可以发现,对于不同的深度,虽然采用的残差模块结构都是以下二者之一。但是残差模块的输入输出维度不一定是相同的,具体来说,有些残差模块输入和输出维度相同,而有些输出时输入的两倍,这是为了数据的升维。所以,在实现残差模块时还需要一个标记,表示该模块是否进行升维。残差模块实现后,ResNet模型就是残差结构的堆叠。
import torch.nn as nn
import torch
class BasicBlock(nn.Module): # 普通残差结构
expansion = 1
def __init__(self, in_channel, out_channel, stride=1, downsample=None, **kwargs):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel,
kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(out_channel)
self.relu = nn.ReLU()
self.conv2 = nn.Conv2d(in_channels=out_channel, out_channels=out_channel,
kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channel)
self.downsample = downsample
def forward(self, x):
identity = x
if self.downsample is not None:
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out += identity
out = self.relu(out)
return out
class Bottleneck(nn.Module):
"""
注意:原论文中,在虚线残差结构的主分支上,第一个1x1卷积层的步距是2,第二个3x3卷积层步距是1。
但在pytorch官方实现过程中是第一个1x1卷积层的步距是1,第二个3x3卷积层步距是2,
这么做的好处是能够在top1上提升大概0.5%的准确率。
可参考Resnet v1.5 https://ngc.nvidia.com/catalog/model-scripts/nvidia:resnet_50_v1_5_for_pytorch
"""
expansion = 4
def __init__(self, in_channel, out_channel, stride=1, downsample=None,
groups=1, width_per_group=64):
super(Bottleneck, self).__init__()
width = int(out_channel * (width_per_group / 64.)) * groups
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=width,
kernel_size=1, stride=1, bias=False) # squeeze channels
self.bn1 = nn.BatchNorm2d(width)
# -----------------------------------------
self.conv2 = nn.Conv2d(in_channels=width, out_channels=width, groups=groups,
kernel_size=3, stride=stride, bias=False, padding=1)
self.bn2 = nn.BatchNorm2d(width)
# -----------------------------------------
self.conv3 = nn.Conv2d(in_channels=width, out_channels=out_channel*self.expansion,
kernel_size=1, stride=1, bias=False) # unsqueeze channels
self.bn3 = nn.BatchNorm2d(out_channel*self.expansion)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
def forward(self, x):
identity = x
if self.downsample is not None:
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += identity
out = self.relu(out)
return out
class ResNet(nn.Module):
def __init__(self,
block, # 残差结构的类别
blocks_num:list, # 列表,每层残差结构的个数
num_classes=1000,
include_top=True,
groups=1,
width_per_group=64):
super(ResNet, self).__init__()
self.include_top = include_top
self.in_channel = 64
self.groups = groups
self.width_per_group = width_per_group
self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2,
padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(self.in_channel)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, blocks_num[0])
self.layer2 = self._make_layer(block, 128, blocks_num[1], stride=2)
self.layer3 = self._make_layer(block, 256, blocks_num[2], stride=2)
self.layer4 = self._make_layer(block, 512, blocks_num[3], stride=2)
if self.include_top:
self.avgpool = nn.AdaptiveAvgPool2d((1, 1)) # output size = (1, 1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
def _make_layer(self, block, channel, block_num, stride=1):
downsample = None
if stride != 1 or self.in_channel != channel * block.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.in_channel, channel * block.expansion, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(channel * block.expansion))
layers = []
layers.append(block(self.in_channel,
channel,
downsample=downsample,
stride=stride,
groups=self.groups,
width_per_group=self.width_per_group))
self.in_channel = channel * block.expansion
for _ in range(1, block_num):
layers.append(block(self.in_channel,
channel,
groups=self.groups,
width_per_group=self.width_per_group))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
if self.include_top:
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return x
def resnet34(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnet34-333f7ec4.pth
return ResNet(BasicBlock, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def resnet50(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnet50-19c8e357.pth
return ResNet(Bottleneck, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def resnet101(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnet101-5d3b4d8f.pth
return ResNet(Bottleneck, [3, 4, 23, 3], num_classes=num_classes, include_top=include_top)
def resnext50_32x4d(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnext50_32x4d-7cdf4587.pth
groups = 32
width_per_group = 4
return ResNet(Bottleneck, [3, 4, 6, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)
def resnext101_32x8d(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnext101_32x8d-8ba56ff5.pth
groups = 32
width_per_group = 8
return ResNet(Bottleneck, [3, 4, 23, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)