Policy Gradient
李宏毅 课堂笔记
PPO(proximal policy optimal)
字面意思是近似策略优化,是policy gradient的一个变形。
先介绍Policy Gradient
一个轨迹可以看做一幕。 或者是游戏的一个回合,在这种情况下是存在终止状态的,但很多情况下都是没有终止状态的, 这时,就不易区分每一幕是个怎么回事。
Trajectory = { s 1 , a 1 , s 2 , a 2 , . . . s T , a T s_1, a_1, s_2 ,a_2,...s_T, a_T s1,a1,s2,a2,...sT,aT}
我们可以根据 P o l i c y π Policy \ π Policy π中的参数 θ \theta θ 来确定轨迹的发生的概率:
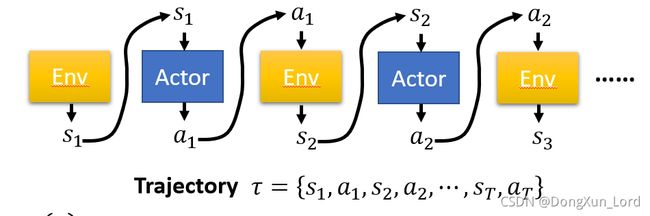
而Policy可以理解为一个包含参数θ 的neutral network,它将Observation中观察到的变量作为输入,将各个可能执行的action的概率向量作为输出,并基于该概率决定下一步要执行的action
这里可以理解为Agent通过观察环境将环境中的一些变量输入 神经网络, 在这里, θ \theta θ扮演的是 n e u t r a l n e t w o r k neutral \ network neutral network中参数的角色, 可以认为它代替了整个的策略 π \pi π (需要注意的是 , 这里NN 同时当做了Actor)
奖励R 是伴随着动作而出现的, 可以将奖励看做一个函数, 它的输入参数就包括了动作 A

动作a的选取必定带有参数 θ \theta θ,这是由于上文中所说的NN决定的, 而更新状态的概率只和前一个时刻的状态和动作有关,这里也体现了马尔科夫性。
既然无法控制外部的环境, 那么只能通过NN as a actor来控制选取的动作, 而一个trajectory里面, 我们知道奖励为:
R ( τ ) = ∑ t = 1 T r t R(\tau)=\sum_{t=1}^Tr_t R(τ)=t=1∑Trt
那么, 接下来的目标就明确了, 就是最大化这个一幕里面的奖励, 但是由于它是一个随机变量(我们的动作的选取和状态都是随机的) 。所以,只能通过调整 θ \theta θ来最大化奖励。
于是, 我们有:
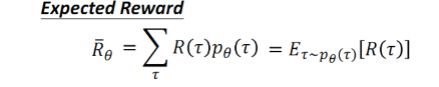
容易理解, 就是在参数 θ \theta θ下, 某个轨迹出现的概率乘以它的累计奖励的和,也就是奖励的期望。
Next: 最大化上面的期望, 用梯度上升法,
即求取上式期望的梯度, 有,
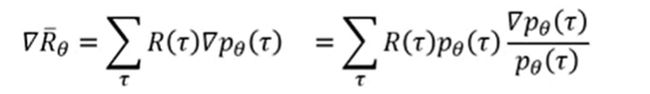
显然, 通过数学公式的转化, 可化为:
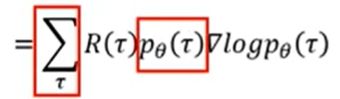
将 p θ ( τ ) p_{\theta}(\tau) pθ(τ)提出写在下面有:
![]()
最后, 抽去N个样本, 即N个trajectory, 可以将上转化为:

这里的 τ n \tau^n τn可以写成上面的式子, 是因为动作是最为关键的,和环境的状态没什么关系。还有一点,上面期望回报的公式中各个量之间是 负反馈的, 即如果在s动作选择动作a的概率大些, 导致了此时的总回报大了, 那么就要更新参数θ让概率更大, 反之,期望变小了, 说明我们选取的动作不好, 就要降低这个概率。
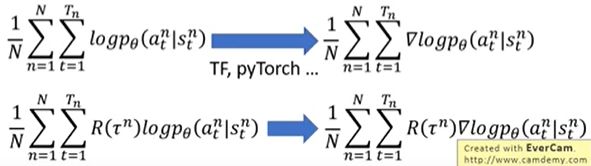
下面进一步的扩展, 梯度上升就体现在了加号上面, 这样更新 θ \theta θ当然还不够, 还有让Agent观察环境、和环境互动来收集数据,如下图所示, 让它玩N个回合的游戏 ,收集奖励值和概率值 ,具体怎么计算在代码中见。
到了这里是整个Policy Gradient的过程, 大概,捋一捋就是通过策略梯度整个大方法, 通过更新参数 θ \theta θ来达到总的期望的奖励最大。
下面是更加具体的实现过程, 也就是用一些工具求取梯度, 输入的是什么, 输出的是什么, 加上一个权重R之后又是什么, 注意这里的R是整幕的汇报, 而不是单单某一step的奖励。
TIP 1 : Add a BaseLine
很多R都是正的, 对更新策略有影响,无法有效更新期望回报, 因为期望是正的, 所以无论怎么做都会提高梯度下的log概率,这样其实也没错, 但是不好,解决方法: 不让你的R总是正的,有:

b就是一个线。 如果R - b是正的,而且还比较大, 那么就让后面的概率变大, 如果一个游戏里面实在没有负数, 那么如果减后值很小, 那么也可以说 这样不好, 我们要减小概率值。
取b = E [ R ( τ ) ] E[R(\tau)] E[R(τ)]也就是 τ n \tau_n τn的平均值, 这样也挺好。
TIP 2 暂时不看了 。后面看Q-learning 再好好理解一下。
MDP 过程(温故而知新):
包含了一些自己的理解, 如果理解有问题或者有想法可以提出来一起讨论
在马尔可夫决策过程中,动作是由智能体决定,所以多了一个成分,智能体会采取动作来决定未来的状态转移。
(类比与小舟有了人的操控和小舟随波漂泊不一样了)
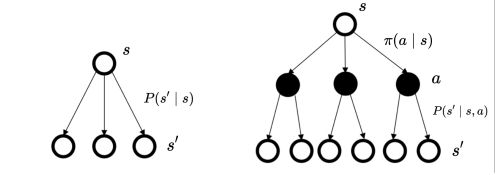
在当前的状态选择一个动作是随机的, 进一步, 选择了动作之后的状态也是一个概率分布, 也是不确定的, 但是在动作哪一步中选择了就是一个决策的过程, 至于怎么选择 是根据策略π来决定的 ,也可以是上面说的Policy gradient 中的将actor当做一个NN来输出一个动作,这样也是可以的, 从这里看, NN的参数θ和策略π还是有一定的关系的。
Bellman 方程 可以理解为 :即时奖励和后续的折扣奖励:
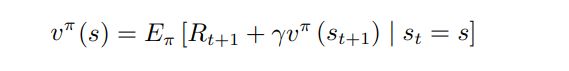

马尔科夫性:一个状态的下一个状态只取决于它当前状态,而跟它当前状态之前的状态都没有关系。
个人认为强化学习很多的概念要不断进行理解才可以掌握, Q-learning可以是RL中最简单的一个算法了, 但是认真捋一遍Q学习的流程和代码发现还是有些地方理解的不到位, 比如策略π到底是个什么东西, 我们当然都知道它是状态到动作的一个映射函数,它最后输出的是一个动作,在Q学习中, 我们采取贪婪策略来进行动作的选择,而这个动作的选择之后就是在Q表中找使Q值最大的动作a然后返回给一个执行学习过程的函数,按照Q学习的伪代码一步一步的执行。
我们还知道, 强化学习训练的目的就是得到一策略函数,在结束训练之后,用这个策略函数来控制智能体;
这个策略函数就叫做目标策略,一个确定的策略是基于值的,在Q学习中选择的动作就是最优的动作,这一点DQN同样适用。
那么有一个问题, 上面说了两个策略, 一个是贪婪策略, 一个是目标策略,这两个策略有什么关系呢,作为初学者,看到这种类似的名词中很容易就搞不明白了。
在强化学习中经常会遇到两个专业术语:同策略 (On-policy) 和异策略 (Off-policy)。
为了解释同策略和异策略,我们要从行为策略 (Behavior Policy) 和目标策略 (Target Policy) 讲起。
在强化学习中,我们让智能体与环境交互,记录下观测到的状态、动作、奖励,用这些经验来学习一个策略函数。在这一过程中,控制智能体与环境交互的策略被称作行为策略。行为策略的作用是收集经验 (Experience),即观测的环境、动作、奖励。行为策略和目标策略可以相同,也可以不同。同策略是指用相同的行为策略和目标策略;异策略是指用不同的行为策略和目标策略;
最常见的行为策略就是贪婪策略,在Q学习中贪婪策略是收集经验中的动作,行为策略和目标策略可以相同,也可以不同。同策略是指用相同的行为策略和目标
贪婪策略:

这是一本书里面介绍的东西, 但是我和学强化学习的师兄讨论了一下, 感觉讲的不太好。可以不看这些乱七八糟的策略, 认为贪婪策略是可以说是一个贪婪算法, 它只是以概率值给出了要进行哪一步, 真正的选择动作a才是真正的策略 .

