【Python三体问题】

周期稳态三体问题

---

三体问题（Three-body problem）是天体力学中的基本力学模型。它是指三个质量、初始位置和初始速度都是任意的可视为质点的天体，在相互之间万有引力的作用下的运动规律问题。例如太阳系中，考虑太阳、地球和月球的运动，它们彼此以万有引力相吸引，若假设三个星球都可设为质点，并且忽略其他星球的引力，太阳、地球和月球的运动即可以视为三体问题。

现在已知，三体问题不能使用解析方法精确求解，即无法预测所有三体问题的数学情景，只有几种特殊情况已研究。对三体问题的数值解，会面临混沌系统的初值敏感问题。

作业题目

---

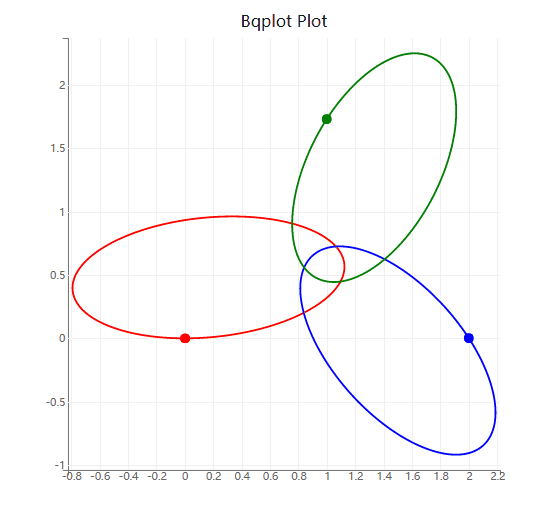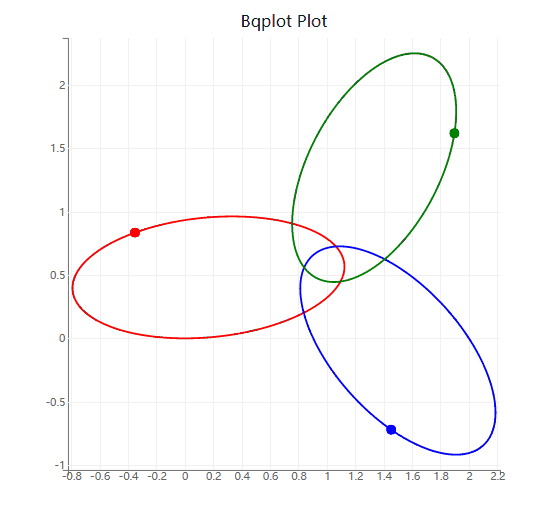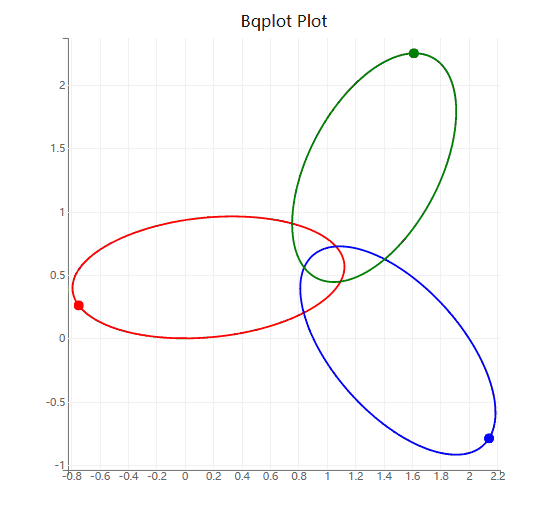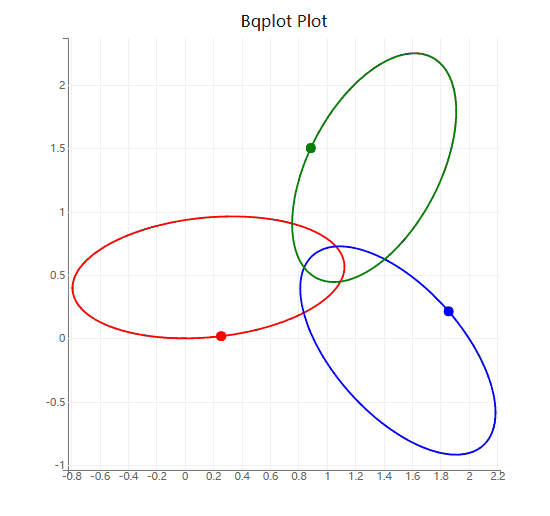
修改下方示例代码的初始条件和求解器参数，计算一个平面三体运动的周期性稳定解，并作图展示。

参考资料

https://observablehq.com/@rreusser/periodic-planar-three-body-orbits

https://numericaltank.sjtu.edu.cn/three-body/three-body.htm

示例代码

---

import numpy as np
from scipy import integrate
def f(t, y, args):
    G, m_A, m_B, m_C = args
    pos_A, pos_B, pos_C, vel_A, vel_B, vel_C = y[:3], y[3:6], y[6:9], y[9:12], y[12:15], y[15:]
    r_AB = np.sqrt(np.sum((pos_A-pos_B)**2))
    r_BC = np.sqrt(np.sum((pos_B-pos_C)**2))
    r_CA = np.sqrt(np.sum((pos_C-pos_A)**2))
    F_A = m_A * m_B * G*(pos_B-pos_A)/r_AB**3 + m_C * m_A * G*(pos_C-pos_A)/r_CA**3
    F_B = m_A * m_B * G*(pos_A-pos_B)/r_AB**3 + m_C * m_B * G*(pos_C-pos_B)/r_BC**3
    F_C = m_A * m_C * G*(pos_A-pos_C)/r_CA**3 + m_C * m_B * G*(pos_B-pos_C)/r_BC**3
    return np.hstack((vel_A, vel_B, vel_C, F_A/m_A, F_B/m_B, F_C/m_C))

G = 10.
m_A = 1.
m_B = 1.
m_C = 1.

args = (G, m_A, m_B, m_C)

pos_A = np.array([0., 0., 0.])
vel_A = np.array([2., 0., 0.])
pos_B = np.array([2., 0., 0.])
vel_B = np.array([-1., np.sqrt(3), 0.])
pos_C = np.array([1., np.sqrt(3), 0.])
vel_C = np.array([-1., -np.sqrt(3), 0.])

'''Initial condition y0 must be one-dimensional'''
y0 = np.hstack((pos_A, pos_B, pos_C, vel_A, vel_B, vel_C))

t = np.linspace(0, 10, 5000)
r = integrate.ode(f)
r.set_integrator('vode', method = 'adams')
r.set_initial_value(y0, t[0])
r.set_f_params(args)

dt = t[1] - t[0]
y_t = np.zeros((len(t), len(y0)))

idx = 0
while r.successful() and r.t < t[-1]+1e-5:
    y_t[idx, :] = r.y
    r.integrate(r.t + dt)
    idx += 1
import bqplot as bq
from bqplot import pyplot as plt

figure = plt.figure(title='Bqplot Plot')
figure.layout.height = '600px'
figure.layout.width = '600px'

plot_A = plt.plot(y_t[:, 0],y_t[:, 1], 'r')  # A
plot_B = plt.plot(y_t[:, 3],y_t[:, 4], 'b')  # B
plot_C = plt.plot(y_t[:, 6],y_t[:, 7], 'g')  # C
scatter_A = plt.scatter(y_t[:2, 0],y_t[:2, 1], colors=["red"])
scatter_B = plt.scatter(y_t[:2, 3],y_t[:2, 4], colors=["blue"])
scatter_C = plt.scatter(y_t[:2, 6],y_t[:2, 7], colors=["green"])

plt.show()

'''Animation'''
import time

idx = 0
speed = 10
T1 = time.time()
i = 0
for idx in range(1, len(t)-1, speed):  # Update Chart
    scatter_A.x = y_t[idx:idx+2, 0]
    x = np.array(y_t[idx:idx+2, 0])
    scatter_A.y = y_t[idx:idx+2, 1]
    y = np.array(y_t[idx:idx+2, 1])
    if ((abs(x[0])<0.015)& (abs(y[0])<0.015)):
        T2 = time.time()
        print(str(i)+'T周期:%s秒'% (T2 - T1))
        i +=1
    scatter_B.x = y_t[idx:idx+2, 3]
    scatter_B.y = y_t[idx:idx+2, 4]
    scatter_C.x = y_t[idx:idx+2, 6]
    scatter_C.y = y_t[idx:idx+2, 7]

    time.sleep(0.01)

参考文献来自桑鸿乾老师的课件：科学计算和人工智能