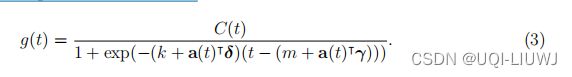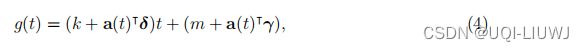论文笔记：Forecasting at Scale（Prophet）
1 时间序列数据的特征
图 2：在 Facebook 上创建的事件数量。 每天都有一个点，点按星期几用颜色编码以显示每周周期。 这个时间序列的特征代表了很多业务时间序列：多重强季节性、趋势变化、异常值、假期效应。
很多时间序列数据都有共同的特征。
图 2 显示了 Facebook 事件的时间序列。 用户可以为事件创建页面、邀请他人参与互动。
在这个时间序列中有几个明显的季节性影响：每周和每年的周期，以及圣诞节和新年前后的明显下降。
与此同时，时间序列在过去六个月中也显示出明显的趋势变化，这可能出现在受新产品或市场变化影响的时间序列中。
最后，真实数据集通常有异常值，这个时间序列也不例外。
1.1 现有方法的局限性
图 3：使用几个不同的时间序列模型对图 2 中的时间序列进行预测。
预测使用的是过去的三个对应时间片的观测值，因而每个点都只使用到这些点的时间序列。（个人理解是周一只用之前三周的周一；周二只用之前三周的周二。。。如此云云）
每天的预测按星期几进行分组和着色，以可视化每周的季节性。
方便起见，我们在绘图期间删除了异常值。
图 3 中的方法通常难以产生与实际的时间序列相匹配的预测。
当截止期附近的趋势发生变化时，自动 ARIMA 预测容易出现大的趋势错误，并且它们无法捕捉任何季节性。
指数平滑（ets)和季节性朴素预测(snaive)捕捉每周季节性，但错过了长期季节性。
所有方法都对年终下降反应过度，因为它们没有充分模拟年度季节性。
当预测不佳时，我们希望能够针对手头的问题调整方法的参数。 调整这些方法需要彻底了解底层时间序列模型的工作原理。
例如，自动化 ARIMA 的第一个输入参数是差分的最大阶数、自回归分量和移动平均分量。 但如何合理地确定这些变量，是一个较为深奥的问题
2 Prophet 模型
我们使用具有三个主要模型组件的可分解时间序列模型：趋势、季节性和假期。 它们组合在以下等式中：
这里 g(t) 是对时间序列值的非周期性变化建模的趋势函数，
s(t) 代表周期性变化（例如，每周和每年的季节性）
而 h(t) 代表假期的影响 发生在一天或多天的潜在不规则时间表。
误差项 εt 表示任何其他的特殊变化； 稍后我们将做参数假设，即 εt 是正态分布的。
2.1 建模趋势
我们实现了两种趋势模型：饱和增长模型和分段线性模型。
2.1.1 非线性，饱和增长模型
对于增长预测，数据生成过程的核心组成部分是关于人口如何增长以及预计如何继续增长的模型。
Facebook 的增长建模通常类似于自然生态系统中的人口增长（例如，Hutchinson 1978），其中非线性增长在承载能力下饱和。 例如，特定区域 Facebook 用户数量的承载能力可能是可以访问 Internet 的人数。
这种增长通常使用逻辑增长模型进行建模，其最基本的形式是
其中 C 是承载能力（最大渐进值），k 是增长率，m 是偏移参数（曲线的终点，等一C/2的位置）。（这是一个(0,C)的取值范围）
Facebook 增长的两个重要方面在（2）中没有体现。
首先，承载能力C不是恒定的——随着世界上可以访问互联网的人数增加，增长上限也随之增加。 因此，我们用随时间变化的容量 C(t) 替换固定容量 C。
二是增速k并非恒定。 新产品可以深刻地改变一个地区的增长率，因此模型必须能够纳入变化的增长率以拟合历史数据。
2.1.1.1 变化增长率的计算
我们通过明确定义允许增长率变化的变化点将趋势变化纳入增长模型
（这里借用一张图，比较好地说明变点的情况）
假设我们由S个趋势增长率变化点，每个变化点
相当于是一个时刻，过了这个时刻变化率就需要变化
所以我们假设基础增长率为k，那么时刻t的实际变化率为
如果我们将所有的
拼接成一个列向量，然后我们在每个时刻k设置一个这样的指示向量a(t)
于是我们时刻t的增长率为： ;?
2.1.1.2 偏移参数的相应增长
设置γj的意思是为了让函数连续，也就是考虑了
所以此时分段逻辑增长模型是
2.1.1.3 承载能力的确定
我们模型中的一组重要参数是 C(t)，即系统在任何时间点的预期容量。 分析师通常可以洞察市场规模，并可以相应地进行设置。 也可能有外部数据源可以提供承载能力，例如世界银行的人口预测。
这里介绍的逻辑增长模型是广义逻辑增长曲线的一个特例，它只是单一类型的 sigmoid 曲线。 将此趋势模型扩展到其他曲线族很简单。
2.1.2 带有变化点的线性趋势
对于不表现出饱和增长的预测问题，分段恒定增长率提供了一个简洁且通常有用的模型。 这里的趋势模型是
这里k是基本增长率，δ是增长率调整向量（和2.1.1.1一样），m是偏移量，γj被设置为
，作用和2.1.1.2一样，也是为了连续
2.1.3 自动变更点选择
变更点 sj 可以由已知的产品发布日期和其他改变增长的事件来指定，或者可以在给定一组候选者的情况下自动选择。
通过在 δ 上放置稀疏先验，可以使用 (3) 和 (4) 中的公式（逻辑斯蒂or线性）很自然地完成自动选择。
我们经常指定大量的变化点（例如，对于几年的时间跨度，每月一个变更点）并使用先验概率分布 δj ∼ Laplace(0, τ )。
先验概率中的参数 τ 直接控制模型改变其速率的灵活性。重要的是，调整 δ 的稀疏先验对主要增长率 k 影响甚小，
当 τ 变为 0 时，拟合会降低到标准（非分段）逻辑或线性增长
2.2 建模季节性
时间序列通常具有多周期季节性。 例如，一周工作 5 天可以对每周重复的时间序列产生影响，而假期安排和学校假期可以产生每年重复的影响。 为了拟合和预测这些影响，我们建模时间序列的季节性特征。
我们使用傅里叶级数来表示周期特点
要建模时间序列的周期性，我们需要预测
这2N个参数
比如我们令![X(t)=[cos(\frac{2\pi(1)t}{T}),cos(\frac{2\pi(2)t}{T}),\dots,cos(\frac{2\pi(N)t}{T}), sin(\frac{2\pi(1)t}{T}),sin(\frac{2\pi(2)t}{T}),\dots,sin(\frac{2\pi(N)t}{T})]](http://img.e-com-net.com/image/info8/e47fc71f2f6d42e7ad9652d1362e7eb2.gif){kind=small}
那么
这里提供一个先验
（σ越大，表示季节的效应越明显）
2.2.1 傅里叶级数N的选择
在 N 处截断序列对季节性应用了低通滤波器，因此增加 N 可以拟合变化更快的季节性模式，尽管过度拟合的风险会增加。
对于每年和每周的季节性，我们发现 N = 10 和 N = 3 分别适用于大多数问题。
当然，可以使用模型选择程序（例如 AIC）自动选择这些参数。
2.3 假期和活动
假期和事件为许多业务时间序列提供了大的、在某种程度上可预测的冲击，并且通常不遵循周期性模式，因此它们的影响无法通过平滑周期很好地建模。 例如，美国的感恩节在 11 月的第四个星期四。 超级碗是美国最大的电视赛事之一，发生在 1 月或 2 月的一个周日。 世界上许多国家都有遵循农历的重大假期。 特定假期对时间序列的影响通常年复一年地相似，因此将其纳入预测非常重要。
我们允许分析师提供过去和未来事件的自定义列表，由事件或假期的唯一名称标识，如表 1 所示。
通过假设假期的影响是独立的，可以直接将这个假期列表合并到模型中。
对于每个假期 i，令 Di 是受该假期影响的过去和未来日期的集合。
我们添加一个指标函数，表示时间 t 是否在假期 i 的影响范围内，并为每个假期分配一个参数 κi，这是预测中的相应变化。
这是通过生成回归量矩阵以与季节性相似的方式完成的
表示当前时刻收到哪些假期的影响（受影响的为1，不受影响的为0）
和周期性类似 ，相应的加和
我们这里提供一个先验
（v越大，表示影响越大）
2.4 模型整体
我们记变更点向量a(t)组成的矩阵为A，那么我们将2.1~2.3 结合一下
在不考虑偏差的情况下 
3 实验部分
图 4 显示了 Prophet 模型对图 3 中 Facebook 事件时间序列的预测。这些预测是在与图 3 中相同的配置进行预测的。（仅使用过去三周相同位置的数据）
Prophet 预测能够预测每周和每年的季节性，与图 3 中的基线不同，它不会对第一年的假期下降反应过度。
在第一个预测中，Prophet 模型在仅给定一年数据的情况下略微过度拟合了年度季节性。 在第三次预测中，模型还没有了解到趋势已经改变。
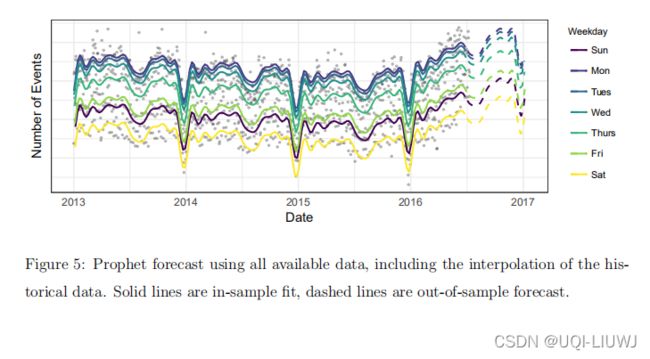
图 5 显示 使用最近三个月数据的预测，将会显示出趋势变化（虚线）。
可分解模型的一个重要好处是它允许我们分别查看预测的每个组成部分。 图 6 显示了与图 4（图注标的是与图5） 中最后一次预测相对应的趋势、每周季节性和年度季节性成分。这为分析师提供了一个有用的工具来深入了解他们的预测问题，而不仅仅是产生 一个预测。
4 总结
4.1 Prophet算法
prophet 算法是基于时间序列分解和机器学习的拟合来做的。不仅可以处理时间序列存在一些异常值的情况，也可以处理部分缺失值的情形，还能够几乎全自动地预测时间序列未来的走势。
prophet 的输入输出是：
- 输入已知的时间序列的时间戳和相应的值；
- 输入需要预测的时间序列的长度；
- 输出未来的时间序列走势。
- 输出结果可以提供必要的统计指标，包括拟合曲线，上界和下界等。
4.2 时间序列分解
做时间序列分解（Decomposition of Time Series）时间序列
分成几个部分，分别是季节项 
，趋势项
，剩余项
。
也就是说对所有的 ，都有
- 加法形式
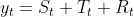
- 乘法形式
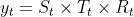
当然，对于乘法形式来说，只要两边同时加log，那么就又转换回了加法形式。