数据结构 排序总结
目录
一、插入排序
1. 直接插入排序
2.希尔排序
二、快速排序
1.冒泡排序
2.快速排序
三、选择排序
1.简单选择排序
2.堆排序
四、归并排序
1. 归并排序(外部)
2. 2路--归并排序(内部)
五、基数排序
1.最低位优先法 LSD
2.链式基数排序
排序分为 内部排序 和 外部排序,其中只有归并排序是外部排序,其余都是内部排序,当然,归并排序也有内部排序的方法。
排序的基本操作包括:比较、移动;
排序算法的稳定性:如果有两个相同的数字,在排序后他们的相对性的位置不会改变,则称这种算法是稳定的。
一、插入排序
1. 直接插入排序
先把当前位置的数字移出去,再与前面的数字进行比较,如果前面的数字大,那么就往后移。
是一种稳定的排序方法,时间复杂度为O(n^2)
for(int i=1; i<=n; i++) cin>>a[i];
for(int i=2; i<=n; i++) {
int t=a[i],j;
for(j=i; j>1; j--) {
if(t折半插入排序的时间复杂度也为O(n^2),查找时采用折半查找的方法
2.希尔排序
从直接插入排序可以看出,若待排序列为有序时,时间复杂度为O(n),插入排序的效率会提高
希尔排序又称为缩小增量排序,方法是先将待排序列分成若干子序列分别进行插入排序,待整个序列基本有序时,再对全体记录进行一次直接插入排序,是一种不稳定的排序方法。
首先取一个gap=n/2,然后再缩小间隔,gap=gap/2,直到gap=1为止。
for(int i=1; i<=len; i++) cin>>a[i];
n=len/2;
while(n) {
for(int k=1; k<=n; k++) {
for(int i=k; i<=len; i=i+n) {
for(int j=i; j>0; j=j-n) {
if(j-n>0&&a[j]>a[j-n]) swap(a[j],a[j-n]);
}
}
}
n=n/2;
}ps:真没觉得哪里简单,写起来反而还更费劲了= =
时间复杂度约为O(n(logn)^2)
二、快速排序
1.冒泡排序
时间复杂度为O(n^2),是一种稳定的排序方法
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;ia[j+1]) swap(a[j],a[j+1]);
}
} 最好情况:只进行一次起泡,做n-1次关键字比较,不进行移动;
最差情况:为恰好逆序的情况,需要执行n-1次气泡。
2.快速排序
取序列中某个关键字作为枢轴量,例如取第一个记录,按照枢轴量的大小将待排序列划分为左右两个序列,左侧都比枢轴量小,右侧都比枢轴量大。
时间复杂度为O(nlogn),是一种不稳定的排序方法,也是所有内部排序中最好的一个
举例:
代码如下:
#include
using namespace std;
int a[100],len;
int quicks(int low,int high) {
int key=a[low];
while(low=key)
high--;
a[low]=a[high];
while(low>t;
while(t--) {
cin>>len;
for(int i=1; i<=len; i++) cin>>a[i];
Qsort(1,len);
for(int i=1; i<=len; i++) cout< 最坏情况:为恰好逆序的情况,时间复杂度为O(n^2)
三、选择排序
1.简单选择排序
第i趟中,找出最小的数与第i个进行交换。
直接选择排序是一种不稳定的排序方法,时间复杂度为O(n^2)
注意:关键字的比较次数与初始序列无关
代码如下:
#include
using namespace std;
int a[100];
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i 2.堆排序
是一种不稳定的排序方法,时间复杂度为O(nlogn)
最大堆:根结点比孩子结点的值大。从小到大排序建立最大堆,从大到小排序建立最小堆。
首先需要创建初始堆:
(1) 根据所给的序列,用数组建树的方法创建一个完全二叉树。
(2) 由最后一个非终端结点(n/2)开始至第一个结点逐步调整。
然后再进行排序:
将根节点的值存储到数组的末尾,然后是一个不断将最后一个叶子结点与根节点进行交换的过程,然后将最后一个叶子结点断开,再重新调成根节点的位置,循环往复。
代码如下:(建立小顶堆)
#include
using namespace std;
int n;
struct Node{
int data=1e9;
int l=0,r=0;
}a[100];
void check(int i) {
if(a[i].data>a[a[i].l].data||a[i].data>a[a[i].r].data) {
if(a[a[i].l].data>a[a[i].r].data) swap(a[a[i].r].data,a[i].data),check(a[i].r);
else swap(a[a[i].l].data,a[i].data),check(a[i].l);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].data;
if(2*i<=n) a[i].l=2*i;
if(2*i+1<=n)a[i].r=2*i+1;
}
for(int i=n/2;i>=1;i--) check(i);
for(int i=n;i>1;i--){
if(i%2) a[i/2].r=0;
else a[i/2].l=0; //将最后一个结点断开
swap(a[1].data,a[i].data); //与根节点进行交换
check(1);
}
for(int i=1;i<=n;i++) cout< 四、归并排序
1. 归并排序(外部)
需要两个被合并的表都有序才行。
#include
using namespace std;
int a[100],b[100],c[200];
int main(){
int n,m,x=1,y=1,k=1;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
cin>>m;
for(int i=1;i<=m;i++) cin>>b[i];
while(x<=n&&y<=m){
if(a[x] 时间复杂度为O(n+m)
2. 2路--归并排序(内部)
将前后相邻的两个有序序列归并为一个有序的序列,不断重复这个操作
是一种稳定的排序方法,时间复杂度为O(nlogn)
#include
using namespace std;
string str[100];
int n;
int main() {
int gap=2;
cin>>n;
for(int i=1; i<=n; i++) cin>>str[i];
while(gap<=n) {
for(int k=1; k<=n/gap; k++)
for(int i=1; i<=gap; i++)
for(int j=(k-1)*gap+1; j<=k*gap-i; j++)
if(str[j].compare(str[j+1])<0) swap(str[j],str[j+1]);
gap*=2;
}
for(int i=1; i<=n; i++) {
for(int j=1; j<=n-i; j++)
if(str[j].compare(str[j+1])<0) swap(str[j],str[j+1]);
}
for(int i=2; i<=n; i++) cout< = =排序看的有点麻了,有什么是不能直接用一个sort解决的..
五、基数排序
1.最低位优先法 LSD
一位一位的排,先排个位,再排十位,再……
跟下面的代码一样
2.链式基数排序
代码如下:
#include
#include
#include
using namespace std;
vector Q[11],a;
int main() {
int flag;
int n;
cin>>n;
for(int i=0; i>num;
a.push_back(num);
}
for(int k=0;; k++) {
int cnt=0;
for(int i=0; i 性能分析:时间复杂度为O(d(n+r)) 其中d:关键字有d位(比如100就是3位数);r:关键字的基数,对r个队列进行收集(其实十位数的基数就是10,0~9一共十个数)
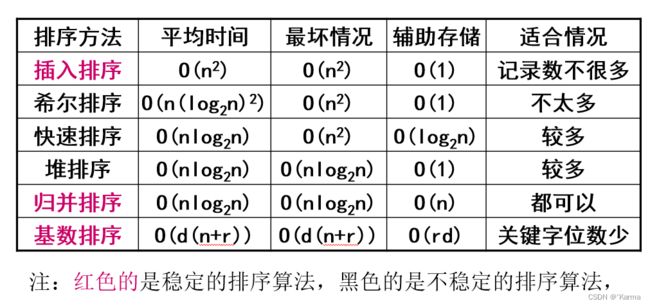
总结
注意:快速排序的空间复杂度为O(logn),为递归过程中,栈所需要的辅助空间。